
bekbaev_energetikadagy_umk_kz_2012
.pdf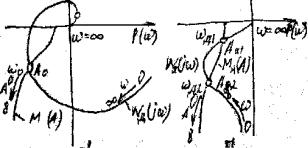
5.1- сурет. Сызықты емес жүйелерде автотербелiстердiң параметрлерiн анықтаудың графикалық тəсiлі
Осы ережеге сүйене отырып 5.1, а жəне б суреттегі үш автотербелістердің 5.1, б суреттегі wa1 жəне Aa1 параметрлі бірінші нүктдегі автотербелістер ғана тұрақты болады.
Статистикалық сызықтау əдісі. j -сызықсыз буын сипаттамасы көрсетілген 5.2 суреттегідей сызықсыз емес жүйені қарастырамыз.
z = j( y) , |
(5.4) |
W ( p) - жүйенiң сызықтық бөлiгiнің берiлiс функциясы.
АРЖ кірісіне mx математикалық күтімі бар жəне s x2 дисперсиялы
тұрақты |
кездейсоқ |
процесi түседi. y(t) шығыс |
сигналының сипаттамаларын |
анықтау қажет: m y |
математикалық күтімді жəне |
s x2 дисперсиясын. |
|
Сызықты емес сипаттаманың статистикалық сызықтауын жасаймыз (5.4) |
|||
|
|
0 |
(5.5) |
|
|
z(t) = k0my + k1 y(t) , |
|
мұнда k0 |
жəне k1 коэффиценттері жалпы жағдайда əлі белгісіз m y жəне s y |
||
шамалардың белгiлi функциялары болып табылады: |
|||
|
k0 = k0 (my ,s y ); k1 = k1 (my ,s y ); |
(5.6) |
|
Сайып келгенде, сызықты емес буынның нəтижесінде де статистикалық сызықтауы m y пайдалы сигналдың жəне əр түрлi күшейту коэффициенттерi бар
0
y (t) инерциясыз күшейткiшiмен ауыстырылады. Пайдалы сигнал жəне кедергі үшiн түзетiлген жүйенiң берiлiс функциялары келесі түде болады
Фy(0) ( p) = W ( p) /[1 + k0W ( p)]; |
(5.7) |
21

Фy(1) |
( p) = W ( p) /[1 + k1W ( p)]. |
(5.8) |
mx = const барысында |
(5.7)-ні қолдана отырып |
|
|
m y = mxW (0) /[1 + k0 (m y ,s y )W (0)]. |
(5.9) |
(5.9) теңдеуі (m y жəне s y ) екі белгісіз шамаға ие |
жəне сондықтан тек |
|
шығыс шамасының дисперсиясынан анықтайтын теңдеумен бірігіп шешілуі мүмкін,
2 |
|
1 |
¥ |
é |
W ( jw) |
ù |
(5.10) |
s y |
= |
|
òS x (w)ê |
|
údw, |
||
2p |
1 + k (m ,s )W ( jw) |
||||||
|
|
|
-¥ |
ë |
1 y y |
û |
|
|
|
|
ê |
ú |
|
||
х + |
|
|
|
|
y |
|
|
|
W ( p) |
||||
– |
z |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Wêá ( p) |
|
|
|
|
5.2- сурет |
|
емес АРЖ |
||||
|
||||||
. Сызықты |
||||||
0
мұнда S x (w) - x(t) - спектрлiк тығыздығы.
(5.9) жəне (5.10) теңдеулерін графикалық əдіспен шешуге болады.
h = my ; |
(5.12) |
h = mxW (0) /[1 + k0 (my ,s y )W (0)]. |
(5.13) |
(5.12) теңдеуге 5.3 а, суретiндегi координаталық my -h |
бұрыштың |
биссектрисасы сəйкес келедi, дəл осы координатада (5.13) теңдеуге параметрi s y бар қисықтар жиыны сəйкес келедi, қисықтар құрастырып, мəндердiң
қатары |
үшiн (5.13) |
тиiстi |
жəне олардың (5.12) түзумен |
қиылысу |
нүктесyi |
|
||||
анықтап табамыз. |
|
|
|
|
|
|
|
|
|
|
Осыдан кейiн табылған |
нүктелер бойыншаm y |
- s y |
координаталарда |
|
||||||
бірінші қисықты құрастырамыз (5.3, б сурет). Дəл осы координаталарда (5.11) |
|
|||||||||
теңдеуі |
бойынша |
екінші |
кисыкты |
құрастырамыз. А нүктесі |
1 |
жəне 2 |
|
|||
қисықтардың қиылысуы iзделiп отырған |
шешiмді бередi. |
|
|
|
|
|||||
Айтылған |
əдiс |
тек |
қана |
мүмкiн |
емес |
автотербелiс |
жүйел |
|||
қолданылады, себебі mx |
тек |
олар болмаған жағдайда ғанаm y |
тұрақтысы |
|
||||||
барысында тұрақты шама бола алады. Сондықтан айтылған əдiсті қолданудан бұрын гармониялық баланс əдiсiмен жасауға болатын автотербелiстердiң пайда болу мүмкiндiгін зерттеу керек. Егер зерттеу жүйеде автотербелiстердiң болуы
22
мүмкiн екенін көрсетсе, онда оның дəлдiгiнiң анықтау үшiн бiрлескен статикалық жəне гармониялық сызықтау əдiсін қолдану керек.
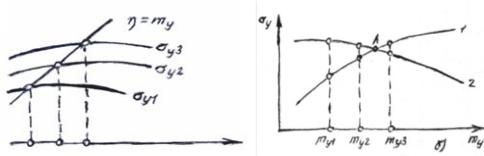
а) б)
5.3- сурет. Теңдеулердiң график түрдегі шешiмi (5.11 ) жəне (5.10 )
Негізгі əдебиеттер: 1 [210-220]. Қосымша əдебиететтер: 1 [365-414]. Бақылау сұрақтары:
1.Сызықты емес элементтiң статистикалық сипаттамасы.
2.Сызықты емес функцияның математикалық күтiмi.
3.Статистикалық сызықтау əдiсінің сызықты емес жүйелерiнiң есептеуi.
Дəрістің тақырыбы 6. Фазалық траекториялар əдiсi
Дəріс конспектісі. Фазалық траекториялардың əдiiс. n -көрсеткішті дифференциалды теңдеу арқылы жазылатын динамикалық жүйенің күйі əрбір уақыт кезеңінде реттелетін шаманың жəне оның(n -1) туындысының мəнімен анықталады. Бұл жүйенің əрбір уақыт кезеңіндегі күйін кейбірn - өлшемді кеңістікте – кескіндейтін нүкте деп аталынатын жеке бірнүктемен көрсетуге болатындығына мүмкіндік туғызады.
Ал мұндай жағдайда, жүйенің күйінің өзгеру процесін осы нүктенің
кеңістіктегі |
қозғалысының |
траекториясы |
ретінде |
қарастыруға . болады |
Сонымен, жүйе күйін кескіндейтін нүктенің жүйе күйі өзгеру процесіне сəйкес |
||||
қозғалыс жолын анықтайтын жолсызықты – фазалық траектория деп атайды. |
||||
Фазалық траекториялар жиынтығын жүйенің |
фазалық |
суретін(жүйенің |
||
фазалық портреті) деп атайды. |
|
|
|
|
Жалпы іс жүзінде көп өлшемді кеңістікті қолдану біраз қиыншылық туғызатындықтан, сызықты емес жүйелерді зерттегенде екі өлшемді фазалық
жазықтықты қолданумен шектеледі. Бұл жағдайда абсцисса өсі |
бойына |
|||
реттелетін y (оның берілген мəнінен ауытқуын) мəнін салады да, ордината |
||||
өсіне z = dy / dt |
мəнін салады. |
|
|
|
Екінші дəрежеліден жоғары емес теңдеумен өрнектелетін АРЖ күйі əрбір |
||||
уақыт сəтінде y |
пен z мəндерімен анықталады да, фазалық жазықтықтағы M |
|||
нүктесімен сипатталынуы мүмкін (6.1-сурет). Өтпелі процесс кезінде y |
пен z |
|||
мəндері |
өзгеріп |
отыратындықтан, фазалық жазықтықта M нүктесі де |
əртүрлі |
|
жерден |
орын |
алады. Осы нүктенің қозғалу траекториясы арқылы |
өтпелі |
|
процесс сипаттамасын анықтайды.
23

Егер y реттелетін |
шаманың берілген мəнінен |
ауытқуы ,болсаонда |
|
орнықты жүйелер үшін орнықты күйдеy = 0 жəне z = 0 , |
яғни t ® ¥ кезде |
||
фазалық траектория координат басына ұмтылуы керек, ал орнықсыз АРЖ |
|||
y(t) |
z |
M |
|
|
|
|
|
M
6.1 - сурет. Уақыттық жəне фазалық жазықтықтардағы жүйенің күйі:
а- уақыт жазықтығы, б-фазалық жазықтық
фазалық траекториясы t ® ¥ кезде координат басынан алыстауы қажет. Фазалық жазықтықтағы фазалық траекториялардан жиналу нүктелерін
(немесе жинақсызданатын нүктелер), ерекше нүктелер деп атайды.
Параметрлік түрде фазалық траекториялар теңдеулер жүйесімен өрнектеледі:
|
dy dt = P( y, z) :ü |
|
(6.1) |
|
|
dz |
ý |
|
|
|
dt = Q( y, z), þ |
|
|
|
мұндағы P( y, z) пен Q( y, z) – y пен z |
мəндері үшін сызықты емес функциялар. |
|||
Екінші теңдеу |
жүйесін(6.1) |
бірінші теңдеуге бөлу арқылы фазалық |
||
траекторияның дифференциалдық теңдеуін аламыз: |
|
|
||
|
dz dy = Q( y, z) / P( y, z) = H ( y, z). |
(6.2) |
||
Айнымалыларды |
бөліп |
жə(6не.2) |
интегралдап, |
фазалық |
траекториялардың тобы үшін жазылған өрнекті аламыз. АРЖ орнықтылығын анықтау үшін ерекше нүктелер маңайындағы(бұл жағдайда-координат басының маңайында) фазалық траекториялардың беталысын қараған жөн. Бұл үшін (6.1) теңдеулер жүйесін сызықтаймыз, яғни оларды Маклорен қатарына түзіп, оның алдыңғы екі мүшесін қарастырсақ, мынаны аламыз:
dy dt = ay + bz; |
(6.3) |
|
dy dt = cy + bz , |
(6.4) |
|
мұндағы a = ¶P ¶y; b = ¶P ¶z; c = ¶Q |
¶y; d = ¶Q ¶y; |
y = z = 0 болғанда. |
(6.3) жəне (6.4) теңдеулерді y |
үшін шешіп, ерекше нүкте маңайындағы |
|
жүйе қозғалысының сызықталған теңдеуін аламыз: |
|
|
y ,, - (a + b) y , + (ad - bc) y = 0 . |
(6.5) |
|
24

Ерекше |
нүкте |
маңайында |
жүйе |
өзгеру |
заңдылығы |
сипаттамалық |
теңдеуінің түбірімен анықталады. |
|
|
|
|
||
|
|
p 2 - (a + b) p + (ad - bc) = 0 |
|
|
(6.6) |
|
Мысалы. Егер теңдеу түбірі жорамал болса, яғни P1, 2 = ± jw , онда
y(t) = A coswt; |
|
(6.7) |
z(t) = y(t) = -Aw sin wt. |
|
(6.8) |
(6.7) мен (6.8) теңдеулерін квадрaттай |
отырып |
жəне бір-біріне қосып |
фазалық траекторияның өрнегін аламыз |
|
|
y 2 / A2 + z 2 / A2w 2 |
= 1. |
(6.9) |
Бұл - эллипстің теңдеуі. Бұл жағдайдағы фазалық траектория мен өтпелі процесс 6.2 - суретте келтірілген. Центр деп аталынатын ерекше нүкте ретіне
координат басы жатады. |
|
Айта кетер жай, фазалық жазықтықта сөнбейтінy(t) |
тербелісіне |
(автотербелісіне) эллипс түрінде болатын фазалық траектория сəйкес болады; былай айтқанда фазалық жазықтықтағы тұйық фазалық траекторияның болуы АРЖ-да автотербелістердің бар екендігінің куəсі.
6.1-кестеде ерекше нүктелердің əртүрлі жағдайлары, атаулары, оларға сəйкес келетін өтпелі процестер мен фазалық траекториялар келтірілген. Бұл кестедегі 1- 3 əр түрлі өтпелі процестер жəне оларға сəйкес келетін фазалық жазықтықтағы фазалық траекториялар.
6.1 - кестеде келтiрiлген фазалық траекториялар нақтылы бір y - z облысы үшiн ғана əдiл. Бұл облысының шектерiнде фазалық траекториялардың бастапқы уақытша теңдеулердегi сызықты байланыстары арқасында маңызды
қалдықтың |
сапалы сипаттарын |
алады. |
Статистикалығы |
сызықты |
емес |
буындардың |
мiнездемелерiнде |
сызықты |
бөлiмшелерге |
бөлектене |
алатын |
сызықты емес АРЖ үшін, əрбiр сызықты бөлiмше үшiн бөлек фазалық
траекториялар құрастыруға болады, |
содан кейін оларды бір бірімен қоса |
аламыз. |
|
z |
y(t) |
y |
t |
6.2 - сурет. Автотербелістің фазалық траекториясы (а) жəне өтпелі процесі (б)
25
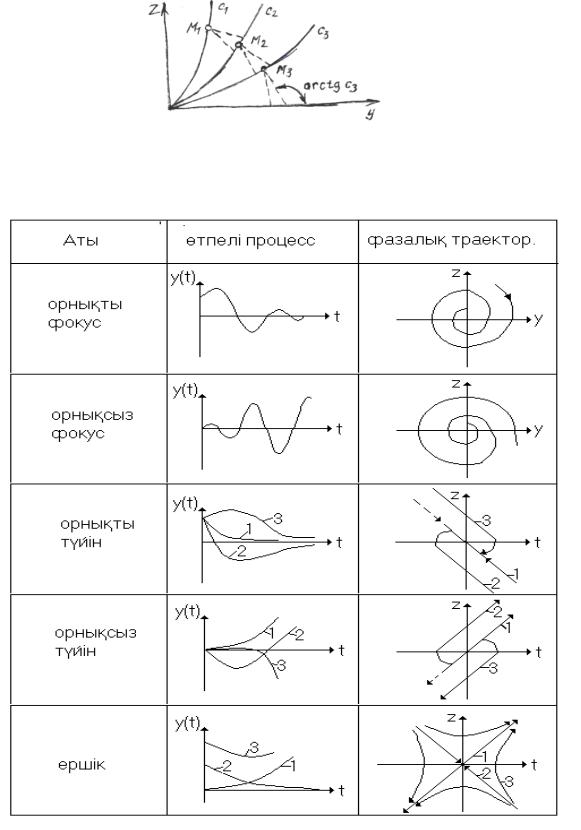
6.3- сурет. Изоклин əдiсімен фазалық траекторияларды құрастыру
6.1 кесте
Ерекше нүктелер
Негізгі əдебиеттер: 3 [324-348]. Қосымша əдебиеттер: 1 [365-414]. Бақылау сұрақтар:
1.Фазалық жазықтық туралы негiзгi ұғымдар.
2.Фазалық жазықтық деген не ?
26
3.Фазалық траектория деген не ?
4.Фазалық кеңiстiк деген не ?
Дəрістің тақырыбы 7. Фазалық траекторияларда изоклин əдiсімен
шектi цикл құрастыру
Дəріс конспектісі. Сызықты емес АРЖ-ң фазалық траекторияларын құрастыруды (6.2) теңдеуiн қолдана отырыпизоклин əдiсімен орындауға болады. Ол үшiн бастапқыда фазалық жазықтықтатөмендегі алгебралық теңдеуге сəйкес келетін сызықтар салады.
H ( y, z) = c = const |
(7.1) |
Əрбiр мəнге изоклин деп аталатын өз сызығы сəйкес келедi (6.3 - сурет). Изоклин - бұл нүкте өтетiн фазалық траекториялардың бiрдей көлбеуi бар геометриялық орны.
dz dy = c = const. |
(7.2) |
7.1- сурет.Шекті циклдердің əр түрлері: |
7.2 – сурет. Фазалық траектория бойынша |
|||||||||||||||
а - тұрақты; б - жартылай тұрақты; |
|
|
ауыспалы процесті құру |
|
||||||||||||
в - тұрақсыз; г - екі шекті цикл: |
|
|
|
|
|
|
|
|
|
|
||||||
(7.2 |
) |
изоклин қасиетін |
пайдалана |
отырып, фазалық |
траекторияларды |
|||||||||||
келесi |
кезекпен |
|
салады. |
с1 |
изоклинінен M1 нүктесін |
аламыз |
|
да |
оданс2 |
|||||||
изоклинімен |
|
қиылысқанға |
|
дейін |
екі |
түзу |
жүргіземіз. Бірінші |
түзуді |
||||||||
с1 изоклинінің |
нүктелеріндегі |
фазалық |
траекториялардың |
|
бұрышына сай |
|||||||||||
arctg c1 |
бұрышымен |
жүргізеді. Екінші |
түзуді c2 |
изоклинінің |
нүктелеріндегі |
|||||||||||
фазалық |
траекториялардың |
бұрышына |
сайarctg c2 бұрышымен |
жүргізеді. c2 |
||||||||||||
изоклиндегi |
M 2 |
нүктесі екі түзуі бар c2 изоклині қиятын жер орнында болады. |
||||||||||||||
Ары қарай |
осы |
тəртіппенM 2 |
нүктесінен |
көлбеу бұрыштарыarctg c2 |
жəне |
|||||||||||
arctg c3 |
екі |
түзу c3 |
изоклинасымен қиылысқанша жүргізіледі, ол |
жерден M 3 |
||||||||||||
нүктесін |
табады. Осылайша |
M1 нүктелерінің |
қатарлары |
табылып, оларды |
||||||||||||
қосқанда АРЖ фазалық траекториясы алынады. |
|
|
|
|
|
|
||||||||||
Сызықты |
|
емес |
АРЖ |
фазалық |
портреттерiнiң |
|
ерекшелi олардаiг |
|||||||||
автотербелiстерге |
сəйкес |
|
келетiншектi |
цикл |
деп |
аталатын |
тұйықталған |
|||||||||
27

фазалық траекториялардың бар болуында. Шектi циклдер тұрақты, жартылай
тұрақты жəне тұрақсыз болады. |
|
|
|
Тұрақты |
шектi цикл |
тұрақты автотербелiстерге |
сə,йкесфазалық |
траекториялар оған (7.1- а сурет,) екi жағынан да жалғанады. Шектi жартылай тұрақты цикл фазалық траекториялар бiр жағынан жалғанып, (7.1- б сурет) басқа жағынан ажыратылатынымен сипатталады. Фазалық траекториялар тұрақсыз шектi циклда (7.1- в сурет,) екi жағынан да ажыратылады. Сызықты
емес АРЖ |
фазалық |
портретi |
(7.1- г сурет) бiрнеше шектi циклдердi иемдене |
алады. |
|
|
|
Екiншi |
реттен |
жоғары |
емес дифференциалды теңдеумен сипатталатын |
сызықты емес АРЖ фазалық портретi дəлдiк, орнықтылық жəне реттеу сапасын қоса əсерлердiң детерминделген күйiндегі сызықты емес жүйенiң динамикасы туралы толық мағлұматты бередi.
Фазалық траектория бойынша өтпелі |
процесс құрастыруға болады. Ол |
||||||
үшiн (7.2 - сурет) келесі амалдар орындалады: |
|
|
|
||||
а) фазалық траектория сызылады; |
|
|
|
||||
б) y(t) = y(nDt) |
құру үшін Dt уақыт қадамы таңдалады, мұнда n - бүтін сан; |
||||||
в) |
b = 2arctg(Dt / 2) бұрышы анықталады; |
|
|
|
|||
г) |
бастапқы |
шарттармен анықталатынy(t) = y0 , нүктесінен a = 900 - b 2 |
|||||
бұрышынан b1 |
нүктесіндегі |
фазалық |
траекториямен қиылысқанша түзу |
||||
жүргізіледі; |
|
|
|
|
|
|
|
д) b1 нүктесінен b |
бұрышы арқылы a1 нүктесіндегі y осімен қиылысқанша |
||||||
түзу жүргізіледі; |
|
|
|
|
|
|
|
e) a1 нүктесін y(t) жазықтығында d1 нүктесіне проекциялайды; |
|
||||||
ж) a нүктесінен a = 900 - b 2 |
бұрышы |
арқылы b |
нүктесіндегі фазалық |
||||
|
1 |
|
|
|
2 |
|
|
траектория мен қиылысқанша түзу жүргізіледі; |
|
|
|
||||
з) b2 нүктесінен b |
бұрышы |
арқылы a2 |
нүктесінде y осімен |
ауысқанша |
|||
түзу жүргізіледі; |
|
|
|
|
|
|
|
и) a2 нүктесін |
y(t) |
жазықтығында проекциялайды, |
осылайша |
y(t) -ң d1 |
|||
нүктелері табылады.
Осылай құрылған y(t) ауыспалы процессі бойынша сызықты емес АРЖ реттеу сапасын əр түрлi бастапқы шартар болғанда объективтi түрде бағалауға болады.
Негізгі əдебиеттер: 1 [134-145]. Қосымша əдебиеттер: 1 [365-414]. Бақылау сұрақтар:
1.Сызықты емес элементтерi бар жүйелердiң фазалық траекториялары.
2.Фазалық траектория бойынша ауыспалы процесстi алу əдiсі.
28
Дəрістің тақырыбы 8. Сызықты емес жүйелердiң орнықтылығы.
Ляпуновтың əдiстерi
Дəріс конспектісі. Ляпуновтың екінші əдісі деп те аталатын Ляпуновтың тікелей əдісін қолданғанда бірінші тəртіп теңдеуі түріндегі автоматты жүйенің дифференциалды теңдеуін қолданамыз. n қатарындағы сызықтық емес жүй үшін бұл теңдеулер мына түрде болады:
|
|
|
|
|
dx1 |
|
= X |
(x , x |
,..., x |
), |
|
|||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
dt |
|
|
|
1 |
|
1 2 |
|
n |
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= X |
2 |
(x , x |
,..., x |
), |
|
(8.1) |
|||||||||
|
|
|
|
|||||||||||||
|
dt |
|
|
1 |
2 |
|
|
n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
…………………… |
|
|
|||||||||||
|
|
dxn |
|
= X |
n |
(x , x |
,..., x ), |
|
|
|||||||
|
|
|
|
|
||||||||||||
|
|
dt |
|
|
|
1 |
|
2 |
|
|
n |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мұнда X1, X 2 ,..., X n функциялары |
|
туынды |
жəне сызықсыздықтың |
кез-келген |
||||||||||||
түріне ие болады бірақ əрқашан |
|
|
|
|
|
|
|
|
|
|
|
|
||||
X1 = X 2 = ... = X n |
= 0 болғанда x1 = x2 = ...xn = 0, |
(8.2) |
||||||||||||||
шартын қанағаттандырады, себебі орныққан жағдайда барлық өтпелі ауытқулар мен туындылар тең болады. Ары қарай бізге келесі мағлұматтар керек болады.
Нақты тұрақты таңбалы жəне қарсы таңбалы функциялар туралы ұғым.
V = V (x1 , x2 ,..., xn ) бірнеше ауыспалының функциясы болсын делік. Үш өлшемді фазалық кеңістікті елестетейік, онда x1, x2 ,..., xn тік бұрышты координаттар
болып табылады (бұл |
негізінен n = 2 кезіндегі фазалық жазықтық жəнеn = 3 |
кезіндегі қарапайым |
үш өлшемді кеңістік болады). Сонда көрсетілген V |
кеңістігінің əр нүктесінде белгілімін болады. Бізге ары қарайV ( x1, x2 ,..., xn ) функциялары керек, олар координаттар басында нөлге айналады жəне(яғни x1 = x2 = ...xn = 0, ) оның айналасындағы кейбір облыстарда үздіксіз болады.
Егер облыстың барлық нүктелерінде координаттар басынан бастап нөлге айналмай, бір ғана таңбаны сақтап тұрса бұл V функциясы нақты деп аталады.
Егер функция бір белгіні сақтап, бірақ басқа облыстарда нөлге айнала алса ол V функциясы тұрақты таңбалы деп аталады.
Егер V функциясы берілген облыстарда түрлі мəндерге ие болса ол қарсы таңбалы деп аталады.
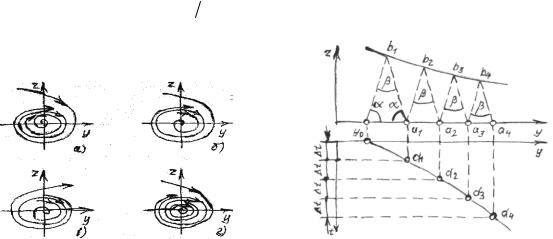
V функцияларының барлық түрлерінің мысалдарын келтіреміз. n = 2 жəне
V = x2 |
+ x2 |
тұрақты таңбалы болады, |
өйткенi тек қана x = 0 |
жəне x |
2 |
= 0 , |
жəне |
||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
V > 0 |
болғанда, |
x1 жəне x2 |
барлық |
нақты мəндердеV = 0 болады. |
Осылайша |
||||||
кез-келген |
n |
мəнде V = x 2 |
+ x2 +... + x 2 |
функциясы |
оң |
тұрақты |
таңбалы, |
||||
|
|
|
1 |
2 |
n |
|
|
|
|
|
|
V = -( x12 + x22 + ... + xn2 ) функциясы теріс тұрақты таңбалы болады.
29
а) |
х3 |
б) |
х3 |
х2 |
в) |
х3 |
|
|
|
|
х1 = -х2
|
|
х2 |
|
х1 |
|
|
|
|
|
|
0 |
0 |
А |
|
|
|
х2 |
||
|
|
|
|
0 |
|
||||
х1 |
|
|
х1 |
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
В |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
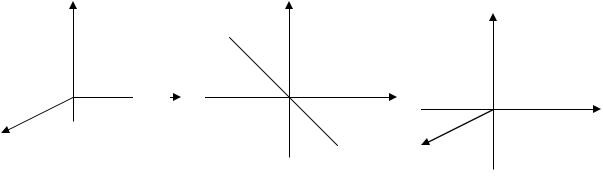
8.1 - сурет. Функцияның үш түрлерiнiң мысалдары |
|
|||||||
Егер |
n = 3 |
болғанда V = x2 |
+ x2 |
функциясын |
алсақ |
ол |
тұрақты |
таңбалы |
|||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
болмайды, |
себебі |
барлық x1, x2 |
жəне x3 кезінде |
ол нөлге |
текx1 = x2 = x3 = 0, |
||||||
кезінде |
ғана |
айналмай, |
x1 = x2 = 0 болса x3 мəнінде |
де айналады. (яғни барлық |
|||||||
осьтер, |
8.1 |
- |
а сурет). |
Демек, |
бұл тұрақты (оң) |
таңбалы |
функция болады. |
||||
Сонымен, |
V = x2 |
+ x2 |
функциясы |
қарсы |
таңбалы |
|
болады, өйткенi |
ол |
|||
|
|
|
1 |
2 |
|
|
|
|
|
|
|
жазықтықтың барлық нүктелерi үшiн x1 = -x2 (8.1 б сурет) түзуінiң оң жағында оң жəне бұл түзуден сол жақта терiс болады.
Бiзге есептердiң кейбiр бөлiндiлерiнде нөлге координаталардың басында
емес, ал АВ түпкi |
кесiндiсінде |
айналатын V функциясының |
керек |
болғанын |
|||
байқаймыз (8.1- в |
сурет). |
Сонда V функцияның айқындығы |
оның |
өзгерiссiз |
|||
таңбасын |
жəне |
кейбiр |
облыстағы бұл |
кесiндiнің |
нөлге |
айналмайтынын |
|
білдіреді. |
|
|
|
|
|
|
|
Ляпунов функциясы жəне оның əр уақыттағы туындысы. |
|
||||||
|
|
|
|
V = V (x1 , x2 ,...xn ), |
|
|
(8.3) |
x1 = x2 = ...xn |
= 0 болғанда нөлге |
айналатын кез |
келген функцияны |
Ляпунов |
|||
функциясы деп атаймыз, егер онда сол айнымалы ауыспалы процесстердегi |
|||||||
ауытқулары x1, x2 ,..., xn шамалар ретiнде алынса |
|
|
|
||||
|
|
x1 = x1 (t) , |
x2 = x2 (t),..., xn |
= xn (t), |
|
|
|
сол жүйе үшiн (8.1) теңдеулері жазылады. Ляпуновтың функциясынан туынды (8.3) əр уақытта
|
|
dV |
= |
¶V |
|
dx1 |
+ |
¶V |
|
dx2 |
+ ... + |
¶V |
|
dxn |
болады. |
|
|
|||||
|
|
dt |
¶x1 dt |
|
|
|
¶xn dt |
|
|
|||||||||||||
|
|
|
|
¶x2 dt |
|
|
|
|
||||||||||||||
Мұнда |
таңдалған |
|
теңдеулерден |
dx |
dx |
n |
|
|
|
мағыналарын |
қоя |
отырып, |
||||||||||
|
1 |
,..., |
|
|
|
|||||||||||||||||
|
|
|
dt |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|||||||
Ляпуновтың функциясынан əр уақытта келесі түрдегі (8.1) туындыны аламыз
30
