книги / Численные методы решения задач строительства. Ч. 2

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Пермский национальный исследовательский политехнический университет

Г.Г. Кашеварова, Т.Б. Пермякова

ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ СТРОИТЕЛЬСТВА

В двух частях

Часть 2

Рекомендовано Учебно-методическим объединением РФ по образованию в области строительства в качестве учебного пособия

для студентов, обучающихся по направлению подготовки «Строительство»

Издательство Пермского национального исследовательского

политехнического университета

2015

1

УДК 69:519.6(075.8) К31

Рецензенты:

д-р техн. наук, профессор П.П. Гайджуров (Ростовский государственный строительный университет); д-р техн. наук, профессор Н.М.Труфанова

(Пермский национальный исследовательский политехнический университет)

Кашеварова, Г.Г.

К31 Численные методы решения задач строительства : учеб. пособие : в 2 ч. / Г.Г. Кашеварова, Т.Б. Пермякова. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2015. – 148 с.

ISBN 978-5-398-01328-3 Ч. 2. – 148 с.

ISBN 978-5-398-01330-6

Изложены основные методы численного решения дифференциальных уравнений, которые имеют большое значение в практике инженерных расчетов, и основы математической теории планированиямногофакторногоэксперимента.

Предназначено для студентов-бакалавров по направлению подготовки «Строительство» может быть использовано студентами других направлений и факультетов, а также инженерами и научными сотрудниками.

УДК 69:519.6(075.8)

2

ПРЕДИСЛОВИЕ

Подготовка бакалавров по профилю «Промышленное и гражданское строительство» направления «Строительство» предусматриваетовладение компетенциями

–в области изыскательской и проектно-конструк-

торской деятельности по расчету и конструированию деталей и узлов с использованием стандартных средств автоматизации проектирования;

–в области экспериментально-исследовательской дея-

тельности по использованию стандартных пакетов автоматизации проектирования и исследований.

Современные специализированные программные комплексы позволяют выполнять расчеты не только задач строительной механики, но и таких физических явлений, как теплопередача, течение жидкостей и газов и др. От расчетчика (пользователя программных комплексов) не требуется детального знания всех математических, вычислительных и компьютерных проблем. Однако ему необходимо иметь представление о том, как математически формулируются эти задачи и что собой представляют численные методы их решения. Без этого трудно рационально выбрать расчетную схему и правильно оценить достоверность окончательных результатов.

Во второй части учебного пособия представлены чис-

ленные методы решения дифференциальных уравнений,

которые имеют большое значение в практике инженерных расчетов, и основы математической теории планирования многофакторного эксперимента.

Множество задач расчета зданий и сооружений приво-

дят к дифференциальным уравнениям – обыкновенным или

в частных производных с разного рода дополнительными

3

условиями: задачами Коши, краевыми или смешанными задачами. При разработке новых или реконструкции существующих строительных объектов приходится решать задачи, связанные с исследованием напряженно-деформированного состояния конструкций, распространения тепла, движения жидкости и газа и др., которые в конечном счете сводятся

крешению дифференциальных уравнений.

Вседьмой главе приводятся примеры задач из практики расчета строительных конструкций, описываемых обыкновенными дифференциальными уравнениями. Рассмотрены наиболее распространенные численные методы решения задач Коши: Эйлера и Рунге-Кутта.

Точное решение краевых задач удается получить лишь для немногих частных случаев. Поэтому наиболее широкое распространение для их решения получили численные методы. Рассмотрен метод конечных разностей, в основе ко-

торого лежит метод сеток, а именно конечно-разностная аппроксимация (КРА) производных в определяющих урав-

нениях задачи. Для решения системы линейных алгебраических уравнений, полученных в результате КРА, пред-

ставлен метод прогонки.

Показана практическая реализация методов Эйлера,

Рунге-Кутта и метода конечных разностей в табличном процессоре Microsoft Excel.

Ввосьмой главе приводятся основные понятия вариационного исчисления, необходимые для понимания вариационных подходов к решению краевых задач. Показана связь решения краевой задачи с нахождением минимума функционала. Рассматривается метод Ритца, который служит для приближенного решения вариационной задачи, позволяющий перейти к методу конечных элементов (МКЭ).

Девятая глава посвящена основам метода конечных элементов в форме метода перемещений, в котором используется вариационный принцип Лагранжа. Область

4

применения метода конечных элементов очень обширна и охватывает практически все физические задачи, которые могут быть описаны дифференциальными уравнениями, как обыкновенными, так и в частных производных. На примерах расчета рамы и плиты в специализированном программном комплексе «ЛИРА» показана практическая реализация метода конечных элементов.

В десятой главе приводятся начальные сведения по

планированию и обработке результатов многофакторных экспериментов, которые позволяют выяснять закономерности влияния разных параметров на показатели качества конструкций и систем. Исследуя поведение сложных конструкций, зданий и сооружений при различных внешних воздействиях, необходимо уделять серьезное внимание ра-

циональной организации экспериментального изучения та-

ких объектов, которое является основным источником получения достоверных сведений об объектах реального мира. Проведение натурных исследований, к сожалению, не всегда можно реализовать на практике. И в этих случаях благодаря широкому внедрению методов математического моделирования и ЭВМ в практику инженерных расчетов на помощь приходит современный способ теоретического исследования – вычислительный эксперимент. Математи-

ческая теория планирования эксперимента позволяет экспериментатору спланировать опыты так, чтобы при минимальной затрате времени и средств получить максимум информации при подготовке и в процессе проведения опытов, а также при обработке результатов эксперимента.

Теоретический материал снабжен большим количеством примеров, которые носят пояснительный характер.

5

ГЛАВА 7

Численные методы решения дифференциальных уравнений

Инженеру-строителю в своей деятельности часто приходится сталкиваться с дифференциальными уравнениями. При разработке новых или реконструкции существующих строительных объектов приходится решать задачи, связанные с исследованием напряженно-деформированного состояния конструкций, распространения тепла, движения жидкости и др., которые в конечном счете сводятся к решению дифференциальных уравнений.

К сожалению, немногие из этих уравнений имеют аналитическое решение, и, чтобы их решить, приходится прибегать к разнообразным численным методам.

В зависимости от числа независимых переменных

дифференциальные уравнения делятся на две категории:

обыкновенные дифференциальные уравнения

(ОДУ), содержащие одну независимую переменную;

дифференциальные уравнения в частных произ-

водных, содержащие несколько независимых переменных.

7.1.Обыкновенные дифференциальные уравнения

врасчетах строительных конструкций

Обыкновенное дифференциальное уравнение n-го порядка в общем виде можно записать как

6

Решение дифференциального уравнения (интегральная кривая) – это функция у = у(х), которая при подстановке в уравнение (7.1) обращает его в тождество.

Общее решение ОДУ (7.1) n-го порядка содержит n постоянных и имеет вид

Если удается найти постоянные С1, С2, …, Сn, определяемые из дополнительных (начальных или краевых) условий, то такое решение называется частным решением.

Для некоторых случаев удается получить точное решение дифференциального уравнения в виде аналитического выражения

Пример аналитического решения дифференциаль-

ного уравнения 1-го порядка

где С – произвольная постоянная.

При различных значениях постоянной С получается семейство интегральных кривых (рис. 7.1).

Если в дополнение к дифференциальному уравнению задать значение у0 для некоторого значения х0, то можно определить постоянную С. Соответствующее ей решение называется частным решением.

Например, предположим, что решение должно проходить через точку с координатами: х = 0, у = 1, что обычно записывается в виде

7

Примером задачи Коши может служить задача о свободных колебаниях одномассовой системы (рис. 7.2).

Здесь в качестве независимой переменной выступает время.

 Если дополнительные условия задаются при двух и более значениях независимой переменной х, то такая задача называется краевой задачей, а дополнительные условия – краевыми

или граничными условиями.

В качестве дополнительных условий в задачах строительной механики стержневых систем обычно использу-

ются условия закрепления концов стержня. Например:

9

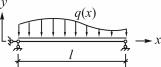
Возможныи другиеболеесложные случаизакрепления.

Исследование напряженного состояния строительных конструкций и связанные с ним расчеты на прочность относятся к наиболее ответственным в строительстве.

Из курса сопротивления материалов известно, что изгиб балки (рис. 7.3) с достаточной степенью точности описывается дифференциальным уравнением 4-го порядка

где EJ – жесткость балки при изгибе.

Известно общее решение этого дифференциального уравнения при EJ = Const и постоянной нагрузке q(x) = p:

Для определения произвольных постоянных здесь требуется четыре дополнительных условия.

Оба конца этой балки при х = 0 и при x = L шарнирно закреплены. Краевые условия задаются при разных значениях независимой переменной х и имеют вид

Уравнение (7.8) и краевые условия (7.10) описывают эту краевую задачу.

Деформированное состояние каждого элемента про-

извольной стержневой системы (рис. 7.4) описывается системой дифференциальных уравнений

10