
книги / Численные методы решения задач строительства. Ч. 2
.pdf
|
d 2w " |
qw f (x), |
||||
EJ |
dx |
2 |
|
|||
|
|
|
|
(7.11) |
||
|
|
|
|
|
||
d 2u |
f |
(x). |
||||
|
2 |
|||||
|
1 |
|
||||
dx |
|
|
|
|
|
|
Здесь |
w |
|
– |
прогиб стержня; |
||
u – удлинение стержня.
В строительной механике при расчете стержневых систем
дифференциальные уравнения не упоминаются, так как при решении интерес обычно представляют частные решения, удовлетворяющие граничным условиям, вид которых известен заранее.
Уравнения строительной механики (канонические уравнения метода сил, метода перемещений и др.) составляются для определения произвольных постоянных, которым придается вполне определенный физический смысл: в методе сил постоянные интегрирования – это силы,
а в методе перемещений – перемещения.
Уравнение устойчивости стерж-
ня постоянного сечения под действием сжимающей силы можно записать в виде
|
d 4 y |
|
|
P d 2 y |
0 |
(7.12) |
|||
|
|
|
|
|
|
||||
|
dx4 |
EJ dx2 |
|||||||
|
|
|
|
||||||
или yIV k2 y" 0. |
|
|
|||||||
Здесь |
k2 |
P |
|
; Р – сжимающая сила; |
|||||
EJ |
|||||||||
Е – |
|
|
|
|
|
||||
модуль |
|
упругости |
материала; |
||||||
J – момент инерции сечения.
Рис. 7.5. К расчету устойчивости стержня
11
7.1.2. Общие замечания о численных методах решения задач строительной механики
Вся история строительной механики до появления компьютеров была ориентирована на численную реализацию той или иной расчетной схемы. Для расчета конструкций с целью избежать большого количества вычислений применялись разные методы и приемы: метод мо-
ментных фокусных отношений, метод упругого центра,
метод Кросса и др. Положение в корне изменилось с появлением компьютеров, которые практически сняли проблему объема вычислений. Можно сказать, что в строительной механике произошла тихая революция, связанная с отказом от многочисленных узкоориентированных приемов и перенесением центра тяжести в инженерной практике на приемы и методы построения компьютерных моделей и применения численных методов, позволяющих решать более широкий спектр задач [7].
Для решения задач Коши и краевых задач, описывае-
мых обыкновенными дифференциальными уравнениями, используют разные численные методы, дающие приближенное решение в виде таблицы значений yi искомой функции y = y(x) для конечного числа значений аргумента в равноудаленных точках заданного отрезка [a, b].
Для этого область изменения аргумента x [a, b] заменяется дискретным множеством точек (узлов) xi, которое называется сеточной областью (разностной сеткой):
n{x0 = a, xi = xi–1 + h, i = 1, 2, …, |
|
n–1, xn = b, h = (b–a)/n}, |
(7.13) |
где i = 0, 1, 2,…, n – номер узла; h – шаг сеточной области. А искомая на [a, b] непрерывная функция y = y(x) на этой сеточной области заменяется функцией дискретного аргумента или таблицей чисел yi = y(xi), (i = 0, 1, …, n),
которая называется сеточной функцией Y{y0 , y1, ..., yn} .
12

Сеточная функция Y{y0 , y1, ..., yn} аппроксимирует точное решение y = y(x) на разностной сетке n [5].
Численные методы не позволяют найти общее решение задачи. Они могут дать только какое-то частное решение.
Это основной недостаток численных методов.
Но зато эти методы применимы к широкому классу дифференциальных уравнений и всем типам задач для них. А с появлением ЭВМ численные методы стали одним из основных способов решения этих задач.
Численные методы можно применять только к корректно поставленным задачам. Задача считается коррект-
ной, если для нее существует решение, оно единственно и непрерывно зависит от входных данных. Численное решение задачи считается корректным, если ее дискретный аналог сохраняет свойства корректности, т.е. полу-
чаемая система алгебраических уравнений имеет единственное решение и оно устойчиво к входным данным (коэффициентам дифференциального уравнения, начальным или граничным условиям).
Основная идея решения дифференциальных уравнений численными методами на ЭВМ заключается в сведении исходной задачи к задаче алгебраической.
7.2. Численные методы решения задачи Коши
Наиболее распространенными методами численного решения задачи Коши являются метод Эйлера и его мо-
дификации – методы Рунге–Кутта [5, 8].
Для обыкновенного дифференциального уравнения n- го порядка
y(n) f (x, y, y', y",..., y(n 1) ) |
(7.14) |
13

задача Коши состоит в нахождении решения y = y(x), удовлетворяющего начальным условиям:
y |
y(x ); |
y ' y'(x |
) ;….; y(n 1) |
y(n 1) (x ) , (7.15) |
|
0 |
0 |
0 |
0 |
0 |
0 |
где x0, y0, y0',…, y0(n – 1) – заданные числа.
Известно [5], что обыкновенное дифференциальное уравнение n-го порядка при помощи замены переменных всегда можно свести к эквивалентной системе n уравнений первого порядка.
Например, дифференциальное уравнение 2-го порядка
y" g( y', y, x) |
(7.16) |
можно заменить эквивалентной системой дифференциальных уравнений 1-го порядка:
z' g(z, y, x), |
(7.17) |
|
y' z, |
|
|
|
|
|
где z – новая переменная.
То есть получена система уравнений относительно у и z. Решение этой системы даст и искомую функцию, и ее произ-
водную.
Методы, которые мы рассмотрим далее, легко обоб-
щаются и на системы уравнений первого порядка.
Таким образом, задачу Коши чаще всего связывают с дифференциальным уравнением первого порядка, и она формулируется следующим образом:
Найти решение дифференциального уравнения y' f (x, y) , удовлетворяющее начальномуусловию
у(х0) = у0.
14
7.2.1. Метод Эйлера
Это простейший численный метод, который основан на разложении функции y в ряд Тейлора в окрестности точки х0:
y(x0 |
h) y(x0 ) hy'(x0 ) |
1 h2 y"(x0 ) |
(7.18) |
|
|
2 |
|
Полагая, что h мало, в методе Эйлера пренебрегают членами второго и высших порядков:
y(x0 h) y(x0 ) hy'(x0 ). |
(7.19) |
Этот вариант численного метода является сравнительно грубым и применяется на практике в основном для ориентировочных расчетов. Однако идеи, положенные в основу методаЭйлера, являются исходнымидляряда другихметодов.
Рассмотрим задачу Коши на примере решения обыкновенного дифференциального уравнения первого порядка
y' f (x, y) |
(7.20) |
с одним начальным условием |
|
у(х0) = у0 |
(7.21) |
на отрезке [a, b] и будем заранее предполагать, что ее ре-
шение существует и единственно.
Введем на отрезке [a, b] равномерную сетку n (7.13) с шагом h. Обозначим через y(xi) точное решение, а через yi – приближенное решение задачи в одинаковых узлах сетки (рис. 7.6).
Из условий задачи (7.20), (7.21) известно, что y(x0 ) y0 , y'(x0 ) f (x0 , y0 ) .
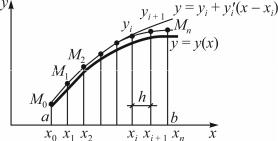
Поэтому можно записать уравнение касательной к графику искомой функции y = y(x) в точке М0(х0, y0) следующим образом:
15
y y0 (x x0 ) f (x0 , y0 ). |
(7.22) |
Рис. 7.6. Геометрическое представление метода Эйлера
Рассмотрим точку М1(х1, у1) – точку пересечения прямой x = x1 = x0 + h и касательной (7.22). При достаточно малом шаге h ординататочкиМ1, определенная поформуле
y1 y0 h f (x0 , y0 ) , |
(7.23) |
мало отличается от y(x1) ординаты решения задачи в точке х1. И точку М1 можно принять приближенно за новую начальную точку, а через нее вновь проводить прямую, которая параллельна касательной к y = y(x) в точке (x1, y(x1)):
y y1 (x x1) f (x1, y1) .
Находя точку пересечения этой прямой и прямой х = х2, получим приближенное значение искомой функции y = y(x) длях= х2, т.е.
y2 y1 h f (x1, y1 ) .
Продолжая этот процесс, получим рекуррентную формулу для вычисления приближенного решения задачи Ко-
ши на сеточной области n:
yi 1 yi h f (xi , yi ), |
i 0,1,..., n 1, |
y0 y(x0 ) . (7.24) |
16

Это равенство означает, что на отрезке [хi, xi+1] инте-
гральная кривая у = у(х) приближенно заменяется прямо-
i= М(xi, yi)
сугловым коэффициентом f(xi, yi).
Вкачестве приближения искомой интегральной кривой получаем ломаную линию с вершинами в точкахлинейным отрезком, выходящим из точки М
М0(x0, y0), М1(x1, y1),…, Мn(xn, yn),
поэтому этот метод иногда называют методом ломаных.
Ошибка метода имеет порядок h2 , так как члены выше второго порядка отбрасываются.
На практике для оценки точности полученного решения, как правило, используют метод половинного шага. Находят численное решение задачи на сетке с шагом h и на сетке с шагом h/2. Если значения полученных решений (двух сеточных функций) в одинаковых узлах отличаются друг от друга не более чем на 1–5 %, то полученную сеточную функцию на второй сетке принимают за приближенное решение задачи Коши. В противном случае шаг уменьшают еще в два раза.
Такая вычислительная схема хорошо программируется для работы на ЭВМ. В частности, эта схема эффективно реализуется с помощью приложения Microsoft Excel и приведена в подразд. 7.2.3.
7.2.2 Метод Рунге–Кутта
Метод Рунге–Кутта является одним из методов повышенной точности. В отличие от метода Эйлера в классическом методе Рунге–Кутта в ряде Тейлора (7.18) учитываются члены до четвертого порядка [5, 8]:
y(x0 h) y(x0 ) hy'(x0 ) 12 h2 y"(x0 )
16 h3 y'"(x0 ) 241 h4 yIV (x0 )
17
Пусть дано дифференциальное уравнение (7.20) с на-
чальным условием (7.21). Строится равномерная сетка n по аргументу х на отрезке [a,b] с шагом h и рассматриваются числа:
k1(i) h f xi , yi ,
k2(i) h f xi h / 2, yi k1(i) / 2 , (i = 0, 1, …, n) (7.25)
k3(i) h f xi h / 2, yi k2(i) / 2 ,
k4(i) h f xi h, yi k3(i) .
Числа k1, k2, k3, k4 имеют простой геометрический смысл – это с точностью до множителя угловые коэффициенты касательных, проведенных к некоторым определяющим точкам искомой функции.
Согласно методу Рунге – Кутта последовательные значения yi искомой функции y = y(x) вычисляются по формуле
yi 1 yi yi ,
|
1 |
(i) |
|
где yi |
6 |
k1 |
|
yi 1
2k2(i) 2k3(i)
|
1 |
(i |
yi |
6 |
k1 |
i 0,1,2,..., n
|
(i) |
, т.е. |
|
|
|
||
k4 |
|
|
|
|
|||
) |
|
(i) |
(i) |
(i) |
, |
|
|
|
2k2 |
|
2k3 |
k4 |
(7.26) |
||
|
|
|
|
|
|
|
|
Метод Рунге – Кутта обладает значительной точно-
стью порядка h5 и, несмотря на некоторую трудоемкость, широко используется при численном решении дифференциальных уравнений с использованием ЭВМ.
Степень точности метода оценивается с помощью алгоритма половинного шага, описанного выше.
Реализация данного метода с использованием таблиц Microsoft Excel приведена в подразд. 7.2.3.
18
7.2.3. Решение задачи Коши с использованием электронных таблиц Microsoft Excel
Алгоритм метода Эйлера
1.Задаем шаг h.
2.Вычисляем значение аргумента xi = x0 + ih при (i =
1, 2, …, n).
3.Последовательно вычисляем приближенные значения решения yi+1 по формуле
yi 1 yi hf (xi , yi ) , (i = 0, 1, … n–1).
Алгоритм метода Эйлера рассмотрим на примере следующей задачи Коши:
y' 2xy, |
y(0) 1. |
(7.27) |
Решение будем выполнять на двух разностных сетках с шагом h = 0,2 и h = 0,1.
Проанализировав полученные приближенные решения, сравним их с имеющимся точным решением y ex2 и сдела-
ем вывод о продолжении или прекращении итерационного процесса.
Последовательность действий
1.Подготовим табл. 1, как показано на рис. 7.7. Зададим значения шага h = 0,2, а = х0 = 0 и у0 = 1.
2.Вычислим значение аргумента (узла) xi = x0 + ih при (i = 1, 2, …, n). Для формирования номера узла n можно использовать «автозаполнение».
3.Последовательно вычисляем приближенные значения
решения y = y(x) в узлах по формуле yi 1 yi hf (xi , yi ) , (i = = 0, 1, … n). Для этого вводим формулы в соответствующие ячейки: С6= F8, С7=С6+2*$F$5*B6*C6 и копируем последнюю доконца таблицы.
19
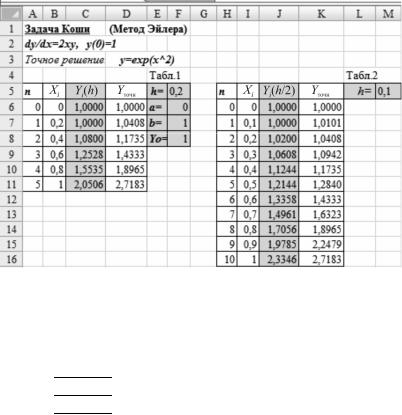
Рис. 7.7. Схема решения задачи Коши методом Эйлера
Таким образом, первое приближенное решение (первая итерация) нашей задачиКошидляшага h = 0,2 имеет вид
Xi |
1,00 |
1,20 |
1,40 |
1,60 |
1,80 |
2,00 |
Yi(h) |
1,00 |
1,00 |
1,48 |
2,31 |
3,79 |
6,51 |
Для оценки точности полученного решения используем метод половинного шага. Уменьшаем шаг вдвое (h = 0,1), повторяем приведенный выше агоритм в табл. 2 на рис. 7.7.
Обе полученные итерации (сеточные функции) нашей задачи Кошина (см. рис. 7.7) тонированы.
Анализ полученных двух приближений (рис. 7.8) показывает, что расхождение их в узле х = 1 составляет более 13 %, поэтому итерационный процесс необходимо продолжить, строить следующую итерацию с шагом h = 0,05.
20
