
- •Лекция 7. Приближенное интегрирование функций.
- •§7.1. Квадратурная формула Ньютона-Котеса.
- •§7.2. Частные случаи квадратурной формулы Ньютона-Котеса.
- •7.2.1. Формула трапеций.
- •7.2.2. Квадратурная формула Симпсона.
- •§7.3. Квадратурная формула Гаусса.
- •§7.4. Приближенное вычисление несобственных интегралов.
- •§7.5. Кубатурные формулы типа Симпсона.
§7.3. Квадратурная формула Гаусса.
Для вывода квадратурной формулы Гаусса потребуются некоторые сведения о полиномах Лежандра.
Определение 7.2.
Полиномы вида
![]()
называются полиномами Лежандра.
Полиномы Лежандра обладают следующими свойствами:
1)
![]() ;
;
2)
![]() ,
где
,
где![]() - любой полином степени
- любой полином степени![]() ,
меньшей
,
меньшей![]() ;
;
3)
полином Лежандра
![]() имеет
имеет![]() различных и действительных корней,
которые расположены на интервале
различных и действительных корней,
которые расположены на интервале![]() .
.
Свойство 2 называется свойством ортогональности полиномов Лежандра.
Перейдем к выводу квадратурной формулы Гаусса.
Рассмотрим
сначала функцию
![]() ,
заданную на отрезке
,
заданную на отрезке![]() .
.
Поставим
задачу: как нужно подобрать точки
![]() и коэффициенты
и коэффициенты![]() ,
чтобы квадратурная формула
,
чтобы квадратурная формула
![]() (7.15)
(7.15)
была
точной для всех полиномов
![]() наивысшей возможной степени
наивысшей возможной степени![]() .
.
Так
как в распоряжении имеется
![]() постоянных
постоянных![]() и
и![]() ,
а полином степени
,
а полином степени![]() определяется
определяется![]() коэффициентами, то эта наивысшая степень
в общем случае равна
коэффициентами, то эта наивысшая степень
в общем случае равна![]() .
.
Для
обеспечения равенства (7.15) необходимо
и достаточно, чтобы оно было верным при
![]() .
.
Действительно, полагая
![]() (7.16)
(7.16)
и
![]() ,
,
будем иметь:
![]() .
.
Таким образом, учитывая соотношения:
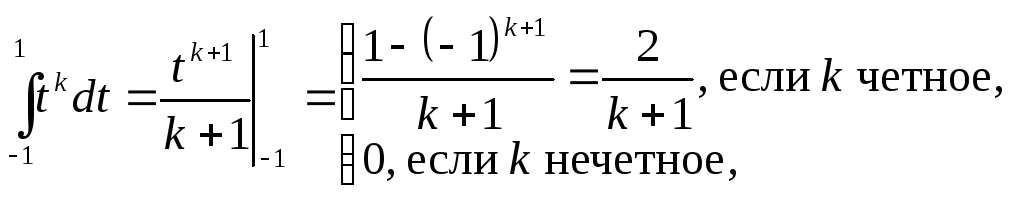
заключаем,
что для решения поставленной задачи
достаточно определить
![]() и
и![]() из системы
из системы![]() уравнений
уравнений
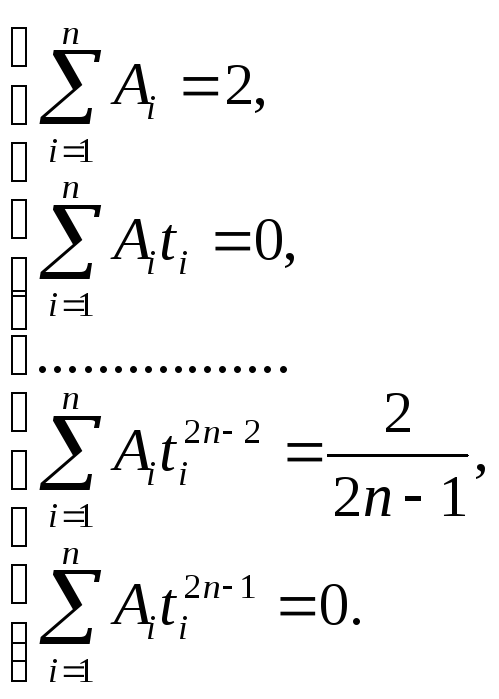 (7.17)
(7.17)
Система
(7.17) – нелинейная система, состоящая из
![]() уравнений с
уравнений с![]() неизвестными
неизвестными![]() и
и![]() .
Решение ее обычным путем представляет
большие математические трудности.
Поэтому применяют искусственный прием.
.
Решение ее обычным путем представляет
большие математические трудности.
Поэтому применяют искусственный прием.
Рассмотрим полином
![]() ,
,
где
![]() - полином Лежандра.
- полином Лежандра.
Так
как степени этих полиномов не превышают
![]() ,
то на основании системы (7.17) для них
должна быть справедлива формула (7.15):
,
то на основании системы (7.17) для них
должна быть справедлива формула (7.15):
![]() .
(7.18)
.
(7.18)
С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены равенства:
![]() ,
при
,
при
![]() ,
,
поэтому в силу (7.18)
![]() (7.19)
(7.19)
Если
положить
![]() ,
то соотношения (7.19) будут выполняться
при любых значениях
,
то соотношения (7.19) будут выполняться
при любых значениях![]() .
.
Таким
образом, для достижения наивысшей
точности квадратурной формулы (7.15) в
качестве точек
![]() достаточно взять нули соответствующего
полинома Лежандра. В силу свойства 3 эти
нули действительны, различны и расположены
на интервале
достаточно взять нули соответствующего
полинома Лежандра. В силу свойства 3 эти
нули действительны, различны и расположены
на интервале![]() .
Подставив найденные значения
.
Подставив найденные значения![]() в систему (7.17), которая при этом становится
линейной, из первых
в систему (7.17), которая при этом становится
линейной, из первых![]() уравнений можно найти коэффициенты
уравнений можно найти коэффициенты![]() .
.
Определитель этой подсистемы является определителем Вандермонда
![]() ,
,
и,
следовательно, коэффициенты
![]() определяются однозначно.
определяются однозначно.
Формула
(7.15), где
![]() - нули полинома Лежандра
- нули полинома Лежандра![]() и
и![]() определяются из системы (3), называется
квадратурной формулой Гаусса.
определяются из системы (3), называется
квадратурной формулой Гаусса.
Неудобство
применения квадратурной формулы Гаусса
состоит в том, что абсциссы точек
![]() и коэффициенты
и коэффициенты![]() - вообще говоря, иррациональные числа.
Этот недостаток отчасти искупается ее
высокой точностью при сравнительно
малом числе ординат.
- вообще говоря, иррациональные числа.
Этот недостаток отчасти искупается ее
высокой точностью при сравнительно
малом числе ординат.
Для
вычисления общего интеграла
![]() по квадратурной формуле Гаусса делают
замену
по квадратурной формуле Гаусса делают
замену
![]() .
.
Тогда
![]() ,
(7.20)
,
(7.20)
где
![]() - нули полинома Лежандра,
- нули полинома Лежандра,![]() .
.
Соотношение (7.20) – квадратурная формула Гаусса для вычисления произвольного интеграла.
Остаточный
член квадратурной формулы Гаусса (7.20)
с
![]() узлами выражается следующим образом:
узлами выражается следующим образом:
![]() .
(7.21)
.
(7.21)
§7.4. Приближенное вычисление несобственных интегралов.
Определение 7.3.
Интеграл
![]() (7.22)
(7.22)
называется собственным, если
промежуток интегрирования
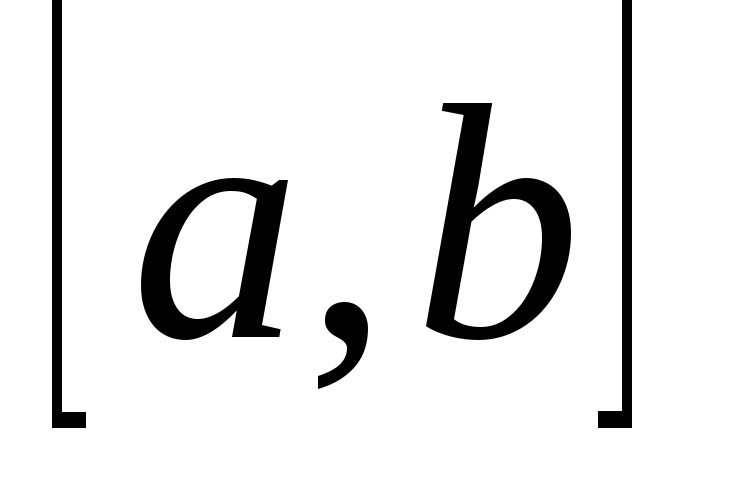 конечен;
конечен;подынтегральная функция
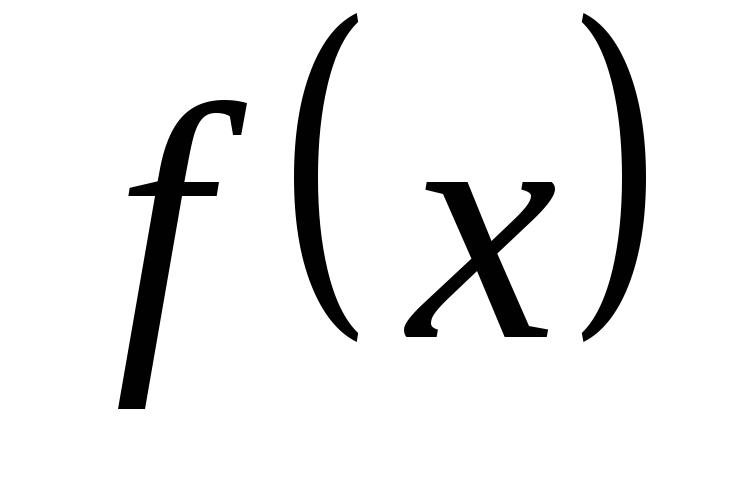 непрерывна на
непрерывна на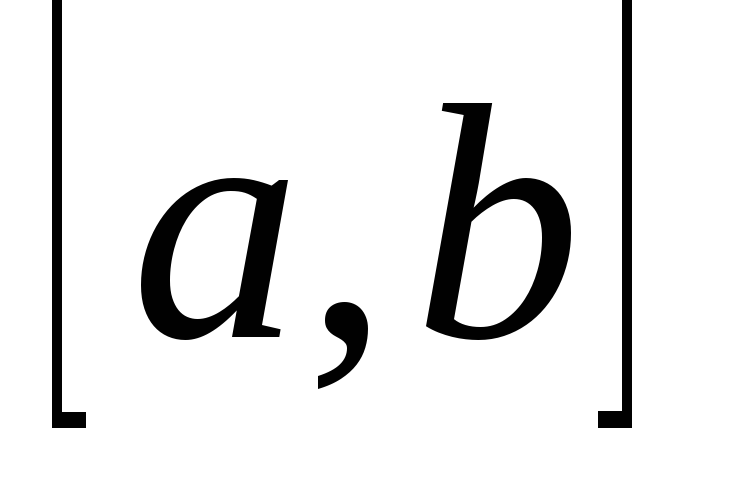 .
.
В противном случае, интеграл (7.22) называется несобственным.
а). Рассмотрим приближенное вычисление несобственного интеграла
![]() (7.23)
(7.23)
с
бесконечным промежутком интегрирования,
где функция
![]() непрерывна при
непрерывна при![]() .
.
Определение 7.4.
Интеграл (7.23) называется сходящимся (Рис.7.3), если существует конечный предел
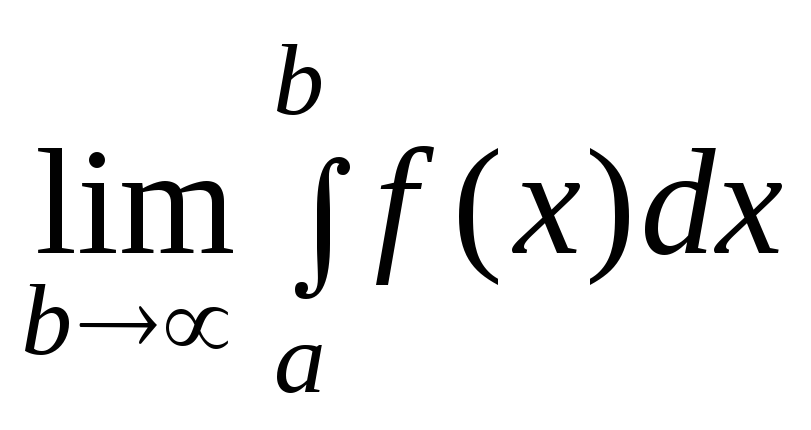 (7.24)
(7.24)
и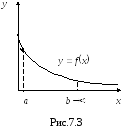 по определению полагают
по определению полагают
 (7.25)
(7.25)
Если предел (7.24) не существует, то интеграл (7.23) называется расходящимся, и такой интеграл считается лишенным смысла. Поэтому, прежде чем приступить к вычислению несобственного интеграла, нужно предварительно убедиться, что этот интеграл сходится.
Чтобы
вычислить сходящийся несобственный
интеграл (7.23) с заданной точностью
![]() ,
представим его в виде
,
представим его в виде
![]() (7.26)
(7.26)
В
силу сходимости интеграла число
![]() можно выбрать столь большим, чтобы имело
место неравенство
можно выбрать столь большим, чтобы имело
место неравенство
![]() (7.27)
(7.27)
Собственный
интеграл
![]() можно вычислить по одной из квадратурных
формул. Пусть
можно вычислить по одной из квадратурных
формул. Пусть![]() - приближенное значение этого интеграла
с точностью до
- приближенное значение этого интеграла
с точностью до![]() ,
т.е.
,
т.е.
![]() .
(7.28)
.
(7.28)
Из формул (7.26)-(7.28) имеем
![]() ,
,
т.е. поставленная задача решена.
б).
Допустим теперь, что отрезок
![]() конечен, а функция
конечен, а функция![]() имеет конечное число точек разрыва на
имеет конечное число точек разрыва на![]() .
Эти точки назовем «особыми» и обозначим
.
Эти точки назовем «особыми» и обозначим![]() .
Такими особыми точками могут быть или
один из концов отрезка, или оба конца
отрезка, либо одна или несколько точек
внутри отрезка.
.
Такими особыми точками могут быть или
один из концов отрезка, или оба конца
отрезка, либо одна или несколько точек
внутри отрезка.
Так
как промежуток интегрирования можно
разбить на частичные промежутки с
единственной точкой разрыва подынтегральной
функции, то достаточно разобрать лишь
случай, когда на
![]() имеется единственная точка разрыва
имеется единственная точка разрыва![]() функции
функции![]() ,
причем второго рода.
,
причем второго рода.
Если
![]() есть внутренняя точка отрезка
есть внутренняя точка отрезка![]() ,
то по определению полагают:
,
то по определению полагают:
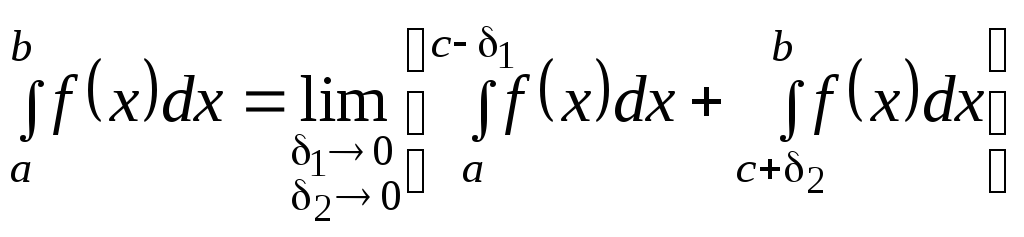 ,
(7.29)
,
(7.29)
и в случае существования этого предела интеграл называют сходящимся, в противном случае – расходящимся.
Аналогично
определяется сходимость несобственного
интеграла, если точка разрыва
![]() подынтегральной функции
подынтегральной функции![]() совпадает с одним из концов промежутка
интегрирования
совпадает с одним из концов промежутка
интегрирования![]() .
.
Для
приближенного вычисления с заданной
точностью
![]() сходящегося несобственного интеграла
(7.29), где точка разрыва
сходящегося несобственного интеграла
(7.29), где точка разрыва![]() ,
выбирают положительные числа
,
выбирают положительные числа![]() и
и![]() столь малыми, чтобы имело место
неравенство:
столь малыми, чтобы имело место
неравенство:
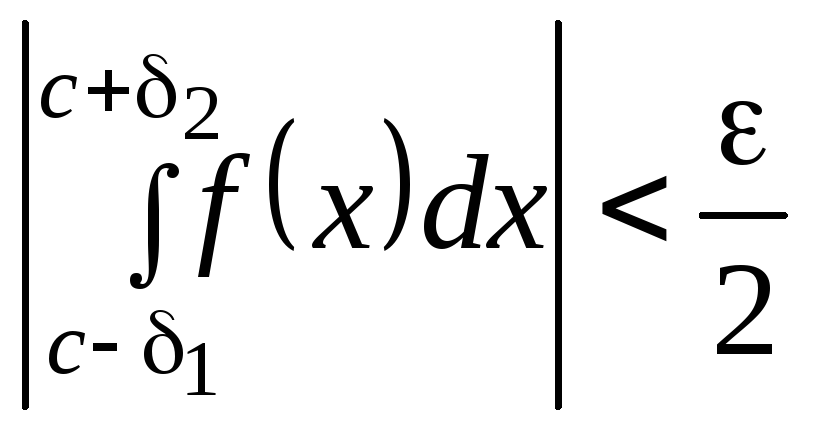 .
.
Затем
по известным квадратурным формулам
вычисляют определенные интегралы
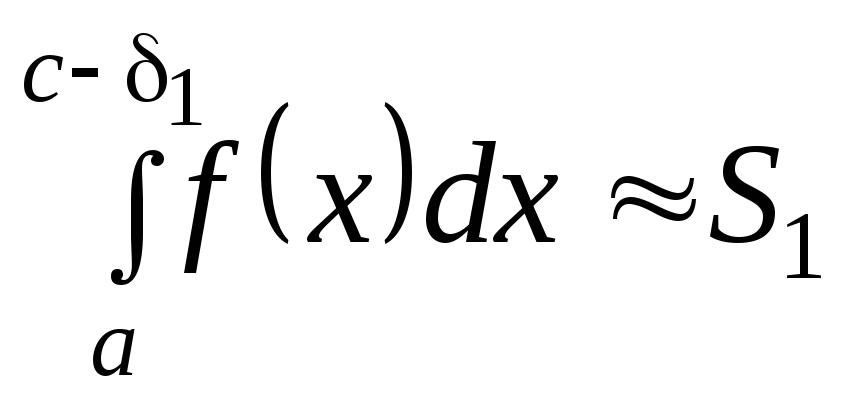 ,
,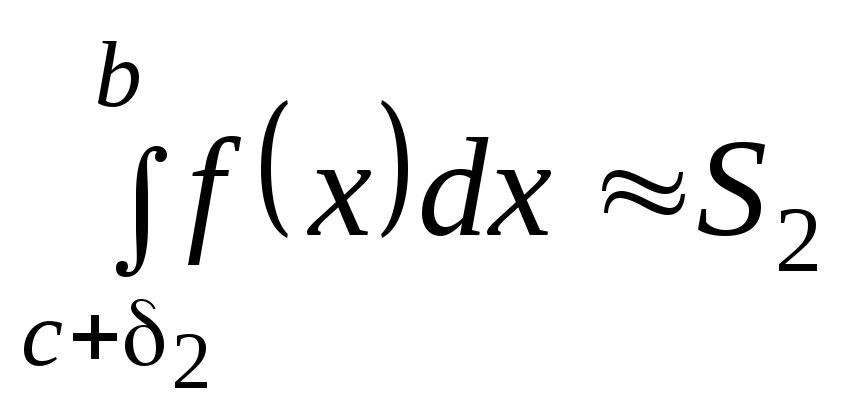 с точностью до
с точностью до![]() .
Тогда
.
Тогда![]() с точностью
с точностью![]() ,
т.е.
,
т.е.
![]() .
.
Если
точка разрыва
![]() подынтегральной функции
подынтегральной функции![]() является концевой для промежутка
интегрирования
является концевой для промежутка
интегрирования![]() ,
то методика вычисления очевидным образом
видоизменяется.
,
то методика вычисления очевидным образом
видоизменяется.
