Лекция 7. Приближенное интегрирование функций.

§7.1. Квадратурная формула Ньютона-Котеса.

Если функция непрерывна на отрезкеи известна ее первообразная, то определенный интеграл от этой функции в пределах отдоможет быть вычислен по формуле Ньютона-Лейбница:

(7.1)

Однако, во многих случаях первообразная не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определенного интеграла по формуле (7.1) может быть затруднено или быть практически невыполнимым. Кроме того, подынтегральная функциячасто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение приобретают численные методы вычисления определенных интегралов, использующие ряд значений подынтегральной функции в точках, где.

Определение 7.1.

Численное вычисление однократного интеграла называется механической квадратурой, двойного интеграла - механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными формулами.

Рассмотрим один из способов вычисления определенных интегралов.

Если воспользоваться, например, интерполяционным полиномом Лагранжа, то, заменяя функцию полиномом, получим равенство

(7.2)

где - ошибка этой интерполяционной формулы.

Требуется вычислить интеграл , где. Выбрав шаг, разобьем отрезокнаравных частей с помощью равноотстоящих точек,,,,. Заменим подынтегральную функциюинтерполяционным полиномом Лагранжаи получим приближенную квадратурную формулу

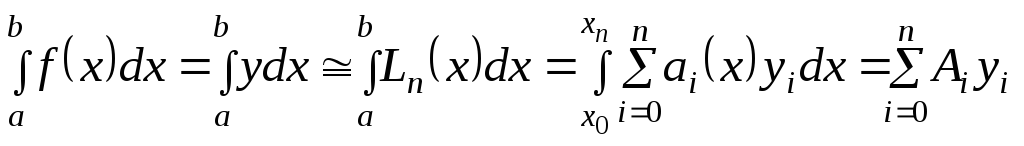, (7.3)

где - некоторые постоянные коэффициенты.

Выведем явные выражения для коэффициентов формулы (7.3). Многочлен Лагранжаимеет коэффициенты

.

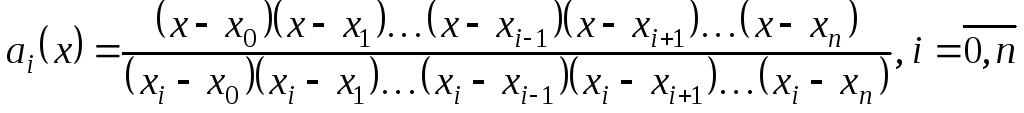Введем обозначения ии с учетом этих обозначений многочлен Лагранжа запишем в виде:

. (7.4)

Заменяя в (7.3) функцию полиномомпо формуле (7.4), получим:

,

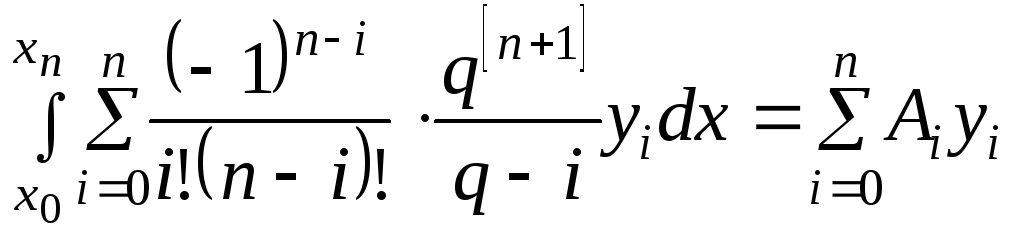где .

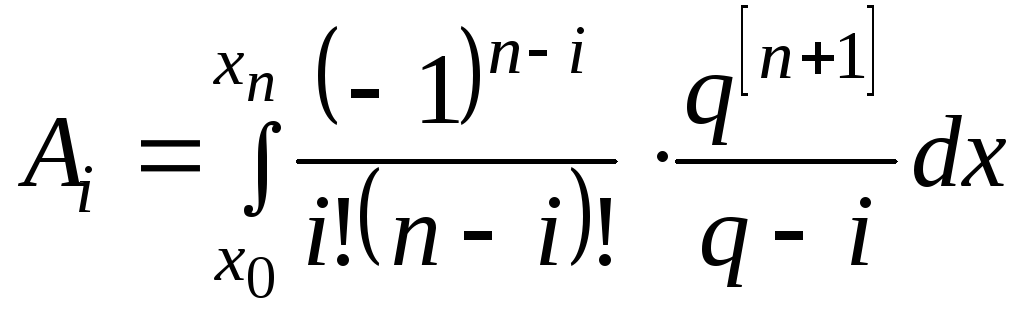Так как и, то сделав замену переменных в определенном интеграле, будем иметь:

.

Так как , где коэффициенты

(7.5)

называются коэффициентами Котеса, то можно записать следующую квадратурную формулу:

(7.6)

Формула (7.6) называется квадратурной формулой Ньютона-Котеса.

Нетрудно проверить, что для коэффициентов Котеса справедливы соотношения:

1) ;

2) .

§7.2. Частные случаи квадратурной формулы Ньютона-Котеса.

7.2.1. Формула трапеций.

а) Пусть отрезок достаточно мал. Положим. Тогда по формуле (7.5) привычислим:

,

,

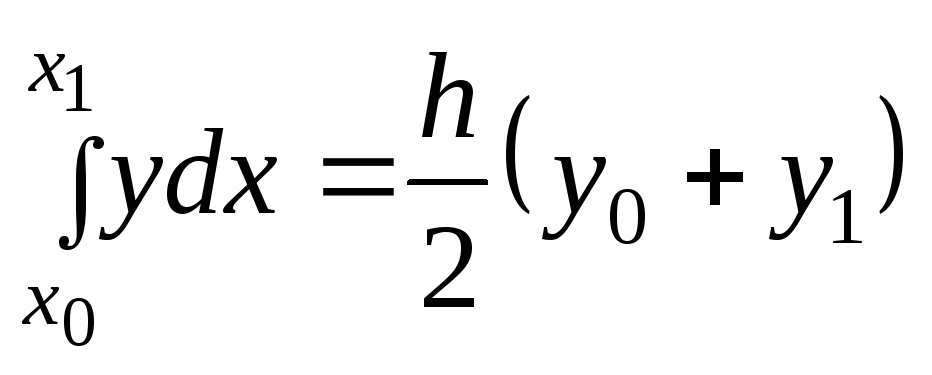. (7.7)

П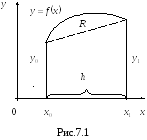олученная формула (7.7) называется формулой трапеций для приближенного вычисления определенного интеграла (Рис.7.1).

Погрешность квадратурной формулы (7.7) равна:

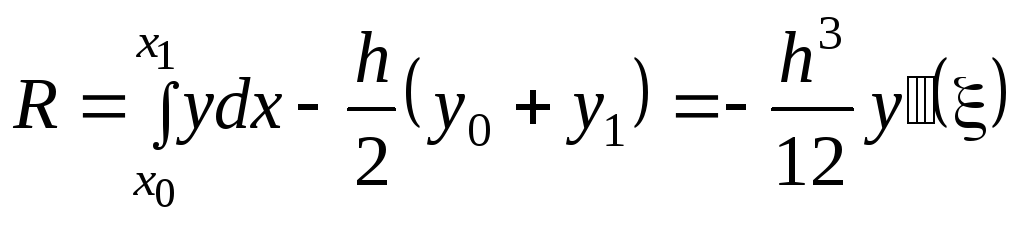, где. (7.8)

Если , то формула (7.7) дает значение интеграла с избытком, если- то с недостатком.

б) Рассмотрим общий случай, когда отрезок произвольной длины.

Разделим отрезок наравных частей,, …,и к каждому из них применим формулу трапеций. Получим:

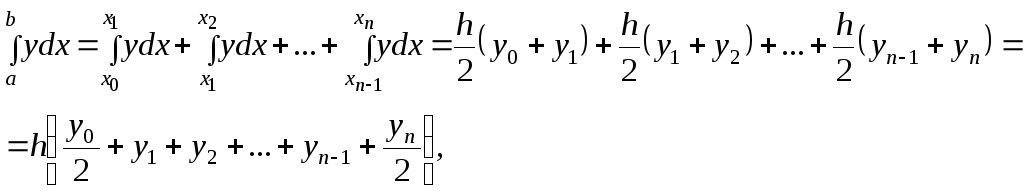(7.9)

где .

Формула (7.9) называется общей формулой трапеций. Для нее справедлива оценка погрешности:

, (7.10)

где ,,.

7.2.2. Квадратурная формула Симпсона.

а) По формуле (7.5) при вычислим коэффициенты Котеса:

,

,

.

Так как , то квадратурная формула для вычисления интеграла примет вид

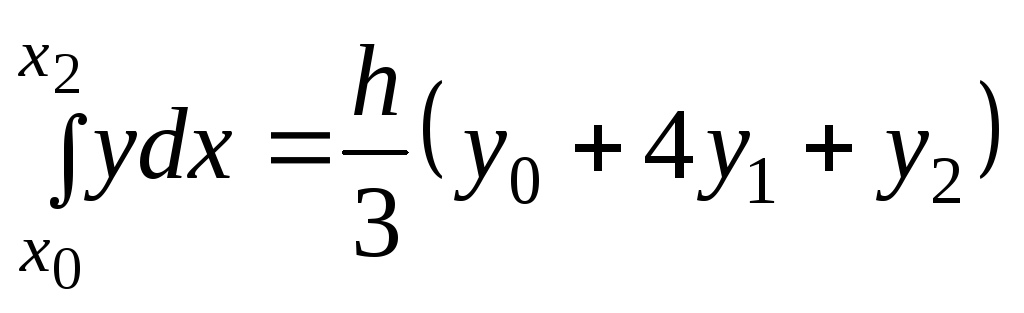. (7.11)

Ф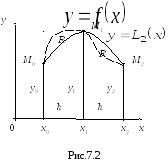ормула (7.11) называется квадратурной формулой Симпсона. Геометрическая интерпретация формулы состоит в том, что происходит замена данной кривойпараболой, проходящей через три точки(Рис.7.2).

Погрешность квадратурной формулы Симпсона равна:

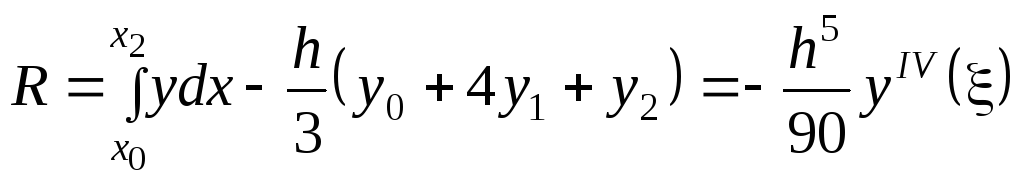, где . (7.12)

Квадратурная формула Симпсона является точной для полиномов второй и третьей степени.

б) Общая формула Симпсона.

Пусть - четное число, и- значения функциидля равноотстоящих точекс шагом,.

Применяя квадратурную формулу Симпсона (7.11) к каждому сдвоенному промежутку ,, …длины, будем иметь:

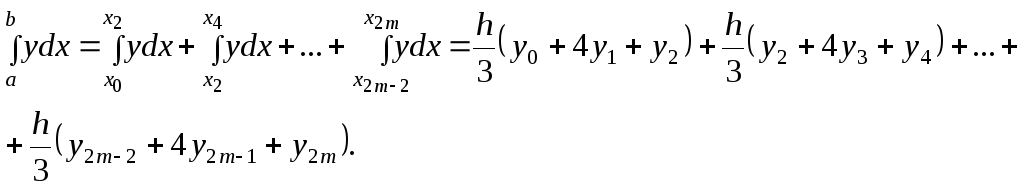
Отсюда получим общую квадратурную формулу Симпсона:

. (7.13)

Остаточный член формулы (7.13) равен:

.

В силу непрерывности на отрезкенайдется точка, такая, что

.

Поэтому будем иметь:

, (7.14)

где .