
Тема 7 Плоские волны в однородной изотропной среде Плоские волны в среде без потерь
Рассмотрим
однородную плоскую волну в среде без
потерь. Свойства среды описываются
абсолютными диэлектрической а
и магнитной а
проницаемостями. Векторы
![]() и
и
![]() однородной плоской волны удовлетворяют
уравнениям Максвелла без сторонних
источников. Поэтому в однородной среде
без потерь
однородной плоской волны удовлетворяют
уравнениям Максвелла без сторонних
источников. Поэтому в однородной среде
без потерь
![]() можно определить из системы уравнений
Максвелла с вещественным волновым
числом
можно определить из системы уравнений
Максвелла с вещественным волновым
числом
![]() (
(![]() ,
где f –
частота колебаний:
,
где f –
частота колебаний:
![]() (1)
(1)
![]()
![]() (2)
(2)
Поскольку
в однородной плоской волне составляющие
![]() могут
зависеть только от одной координаты z,
перпендикулярной плоским волновым
поверхностям, то уравнение (1) примет
вид:
могут
зависеть только от одной координаты z,
перпендикулярной плоским волновым
поверхностям, то уравнение (1) примет
вид:
![]() ,
,
![]() ,
,
![]() (3)
(3)
Дифференциальные
уравнения второго порядка для
![]() и
и
![]() (3) имеют общие решения:
(3) имеют общие решения:
![]() ,
,
![]() (4)
(4)
где
![]() – произвольные постоянные интегрирования,
представляющие собой комплексные
амплитуды вектора поля при z = 0
(например,
– произвольные постоянные интегрирования,
представляющие собой комплексные
амплитуды вектора поля при z = 0
(например,
![]() ).
).
Подставляя
(4) в (2), определим составляющие
![]() :
:
![]() ,
,
![]() ,
,
![]() (5)
(5)
П
Рис.13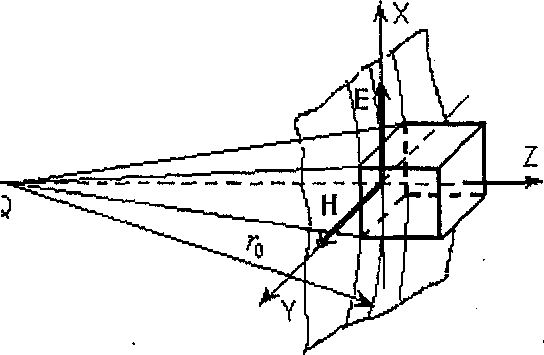
![]() и
и
![]() требуется
знать только в области
требуется
знать только в области
![]() ,
размеры которой малы по сравнению с
расстоянием до источника (
,
размеры которой малы по сравнению с
расстоянием до источника (![]() ).
Введем декартову систему координат
).
Введем декартову систему координат
![]() ,
ось
,
ось
![]() которой
проведена вдоль радиуса-вектора,
соединяющего середину вибратора
которой
проведена вдоль радиуса-вектора,
соединяющего середину вибратора
![]() с
точкой
с
точкой
![]() ,
принятой за начало координат (рис. 13). В
пределах области
,
принятой за начало координат (рис. 13). В
пределах области
![]() можно пренебречь изменением амплитуд
векторов
можно пренебречь изменением амплитуд
векторов
![]() и
и
![]() и, кроме того, считать, что их фазы зависят
только от координаты
и, кроме того, считать, что их фазы зависят
только от координаты
![]() ,
т.е.
считать, что
,
т.е.
считать, что
![]() ,
a
,
a
![]() Запишем:
Запишем:
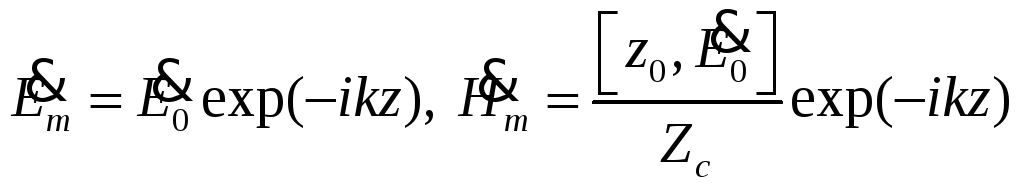 (6)
(6)
С
![]() и
и
![]() перпендикулярны
друг другу и направлению распространения
волны (оси
перпендикулярны
друг другу и направлению распространения
волны (оси
![]() ).
Ориентация
векторов
).
Ориентация
векторов
![]() и
и
![]() относительно
осей
относительно
осей
![]() и м зависит от ориентации источника,
создающего поле. В общем случае эти
векторы могут иметь как
и м зависит от ориентации источника,
создающего поле. В общем случае эти
векторы могут иметь как
![]() -ю,
так и
-ю,
так и
![]() -ю
составляющие, связанные соотношениями
-ю
составляющие, связанные соотношениями
![]() (7)
(7)
Поверхности
равных фаз (ПРФ) в данном случае
определяются уравнением
![]() ,
т.е.
представляют собой плоскости,
перпендикулярные оси
,
т.е.
представляют собой плоскости,
перпендикулярные оси
![]() .
Волну, ПРФ которой образуют семейство
параллельных создаваемую ЭЭВ, в пределах
области
V можно
рассматривать как плоскую волну
плоскостей, называют
плоской волной.
.
Волну, ПРФ которой образуют семейство
параллельных создаваемую ЭЭВ, в пределах
области
V можно
рассматривать как плоскую волну
плоскостей, называют
плоской волной.
2. Свойства плоской волны в однородной изотропной среде
Исследуем
основные свойства плоской волны,
распространяющейся в безграничной
однородной изотропной среде. Источники,
создающие волну, находятся за пределами
рассматриваемой области. Поэтому векторы
![]() и
и
![]() удовлетворяют однородным уравнениям
Гельмгольца. Предположим, что поле не
зависит от координат
удовлетворяют однородным уравнениям
Гельмгольца. Предположим, что поле не
зависит от координат
![]() и
и
![]() .
Тогда уравнения принимают вид
.
Тогда уравнения принимают вид
![]() (8)
(8)
где
![]() .
Решая
уравнение для вектора
.
Решая
уравнение для вектора
![]() ,
получаем
,
получаем
![]() (9)
(9)
где
![]() и
и
![]() - некоторые векторные, в общем случае
комплексные, постоянные.
- некоторые векторные, в общем случае
комплексные, постоянные.
Считаем, когда потери в среде обусловлены только ее проводимостью, введем обозначение
![]() (10)
(10)
получаем
![]() .
Отметим, что
.
Отметим, что
![]() больше величины
больше величины
![]() в среде без потерь с теми же значениями
в среде без потерь с теми же значениями
![]() и
и
![]() .
Аналогично, обозначая
.
Аналогично, обозначая
![]() (11)
(11)
получаем
![]() .
.
Рассмотрим
волну в момент
![]() в точке
в точке
![]() фаза напряженности электрического
поля, соответствующего этой волне, равна
фаза напряженности электрического
поля, соответствующего этой волне, равна
![]() .
В момент
.
В момент
![]() в точке
в точке
![]() фаза той же функции равна
фаза той же функции равна
![]() .
Полагая
.
Полагая
![]() ,
приходим к соотношению
,
приходим к соотношению
![]() .
Как видно, положительным приращениям
.
Как видно, положительным приращениям
![]() соответствуют положительные приращения
соответствуют положительные приращения
![]() .
Следовательно, такая волна распространяется
в положительном направлении оси
.
Следовательно, такая волна распространяется
в положительном направлении оси
![]() .
.
Предположим,
что источник, создающий электромагнитное
поле, расположен со стороны отрицательных
значений
![]() (рис.13).
Так как среда считается безграничной
и однородной, в рассматриваемой области
пространства должна существовать только
волна, распространяющаяся в положительном
направлении оси
(рис.13).
Так как среда считается безграничной
и однородной, в рассматриваемой области
пространства должна существовать только
волна, распространяющаяся в положительном
направлении оси
![]() .
Поэтому
в первом слагаемом в формуле (11) в
соответствии с выбором вида множителя
.
Поэтому
в первом слагаемом в формуле (11) в
соответствии с выбором вида множителя
![]() следует
положить
следует
положить
![]() (12)
(12)
При
выбранном значении
![]() второе слагаемое в (9) описывает волну,
распространяющуюся к источнику. Так
как среда является однородной, то
второе слагаемое в (9) описывает волну,
распространяющуюся к источнику. Так
как среда является однородной, то
![]() .
Следовательно
.
Следовательно![]() .
.
Аналогично,
из уравнения Гельмгольца для вектора
![]() находим, что
находим, что
![]() ,
где
,
где
![]() -
некоторый постоянный (в общем случае
комплексный) вектор. Непосредственно
из уравнений Гельмгольца дополнительной
информации о векторах
-
некоторый постоянный (в общем случае
комплексный) вектор. Непосредственно
из уравнений Гельмгольца дополнительной
информации о векторах
![]() и
и
![]() получить нельзя. Однако векторы
получить нельзя. Однако векторы
![]() и
и
![]() должны
удовлетворять уравнениям Максвелла.
Так как векторы
должны
удовлетворять уравнениям Максвелла.
Так как векторы
![]() и
и
![]() не
зависят от переменных
не
зависят от переменных
![]() и
и
![]() ,
то, проецируя указанные уравнения на
ось
,
то, проецируя указанные уравнения на
ось
![]() ,
замечаем,
что
,
замечаем,
что
![]() и
и
![]() .
Таким образом, и в случае
.
Таким образом, и в случае
![]() векторы
векторы
![]() и
и
![]() перпендикулярны
направлению распространения волны.
Такие волны называют
поперечными.
Проецируя затем уравнения на оси X и У,
приходим к соотношениям
перпендикулярны
направлению распространения волны.
Такие волны называют
поперечными.
Проецируя затем уравнения на оси X и У,
приходим к соотношениям
![]() ,
,![]() ,
из которых следует, что
,
из которых следует, что
![]() (13)
(13)
где
![]() -
характеристическое сопротивление волны
(отношение поперечных к направлению
распространения волны составляющих
векторов
-
характеристическое сопротивление волны
(отношение поперечных к направлению
распространения волны составляющих
векторов
![]() и
и
![]() ).
У волны, распространяющейся в среде с
потерями,
).
У волны, распространяющейся в среде с
потерями,
![]() -
комплексное число. В рассматриваемом
случае
-
комплексное число. В рассматриваемом
случае
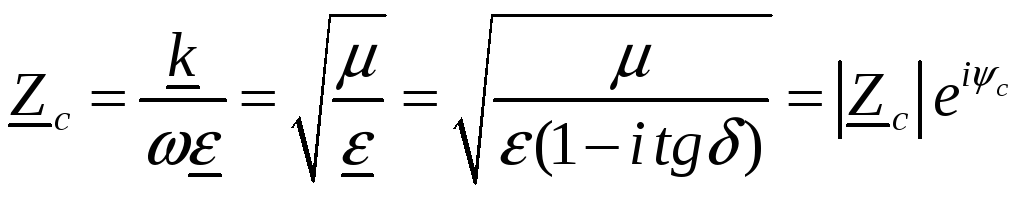 (14)
(14)
где
![]() ;
;
![]() (15)
(15)
В
среде без потерь
![]() и
и
![]() ;
;
![]() .
.
Таким образом, поле плоской волны в среде с проводимостью, отличной от нуля, определяется выражениями
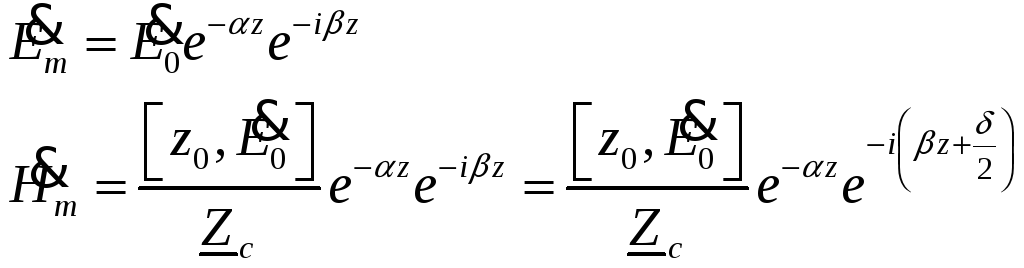
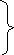 (16)
(16)
В
среде без потерь
![]() ,
,
![]()
При
изменении удельной проводимости от
нуля до бесконечности угол
![]() увеличивается от нуля до
увеличивается от нуля до
![]() ,
а модуль
,
а модуль
![]() убывает от
убывает от
![]() до
нуля. Как видно, наличие потерь приводит
к уменьшению абсолютной величины
характеристического сопротивления,
т.е. к увеличению
до
нуля. Как видно, наличие потерь приводит
к уменьшению абсолютной величины
характеристического сопротивления,
т.е. к увеличению
![]() при заданном значении
при заданном значении
![]() .
Это обусловлено тем, что величина
.
Это обусловлено тем, что величина
![]() определяется как током проводимости,
так и током смещения. В среде без потерь
существуют только токи смещения. В среде
с потерями при тех же значениях
определяется как током проводимости,
так и током смещения. В среде без потерь
существуют только токи смещения. В среде
с потерями при тех же значениях
![]() и
и
![]() токи смещения остаются прежними, но к
ним добавляются токи проводимости.
токи смещения остаются прежними, но к
ним добавляются токи проводимости.
Проанализируем
полученные результаты. Рассмотрим
сначала случай, когда вектор
![]() имеет лишь одну составляющую, например,
имеет лишь одну составляющую, например,
![]() .
Тогда вектор
.
Тогда вектор
![]() также будет иметь одну составляющую,
перпендикулярную
также будет иметь одну составляющую,
перпендикулярную
![]() (в рассматриваемом примере
(в рассматриваемом примере
![]() ).
Считая вектор
).
Считая вектор
![]() вещественным
(
вещественным
(![]() )
и переходя к мгновенным значениям
векторов
)
и переходя к мгновенным значениям
векторов
![]() и
и
![]() из получаем
из получаем
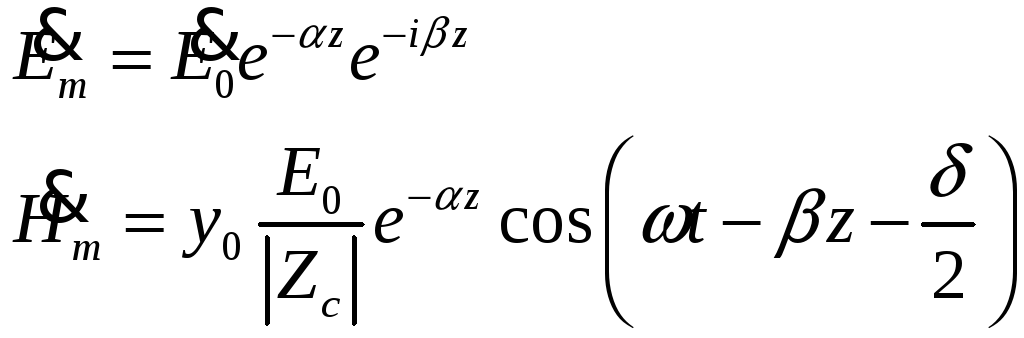
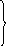 (17)
(17)
В случае среды без потерь формулы принимают вид
![]() (18)
(18)
Из
полученных формул видно, что поле плоской
волны в однородной изотропной среде
обладает следующими свойствами. Волна
является поперечной. Комплексные
амплитуды (![]() и
и
![]() )
векторов
)
векторов
![]() и
и
![]() всегда взаимно перпендикулярны, а в
частном случае, когда вектор
всегда взаимно перпендикулярны, а в
частном случае, когда вектор
![]() имеет одну составляющую (например,
имеет одну составляющую (например,
![]() ),
взаимно перпендикулярны и их мгновенные
значения. Поверхности равных фаз
определяются уравнением
),
взаимно перпендикулярны и их мгновенные
значения. Поверхности равных фаз
определяются уравнением
![]() и
представляют собой семейство плоскостей,
перпендикулярных оси
и
представляют собой семейство плоскостей,
перпендикулярных оси
![]() .
Амплитуды
векторов
.
Амплитуды
векторов
![]() и
и
![]() экспоненциально
убывают вдоль оси
экспоненциально
убывают вдоль оси
![]() .
Постоянную
.
Постоянную
![]() называют
коэффициентом ослабления.
В среде без потерь
называют
коэффициентом ослабления.
В среде без потерь
![]() и
и
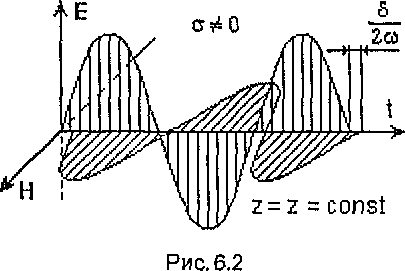
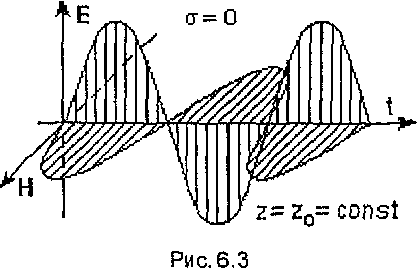
Рис.14
Рис.15
амплитуды
векторов
![]() и
и
![]() не зависят от координат. При
не зависят от координат. При
![]() поверхности равных амплитуд (ПРА)
совпадают с ПРФ. Волны, обладающие таким
свойством, как и волны, амплитуды векторов
поверхности равных амплитуд (ПРА)
совпадают с ПРФ. Волны, обладающие таким
свойством, как и волны, амплитуды векторов
![]() и
и
![]() которых не зависят от координат, называют
однородными.
При
которых не зависят от координат, называют
однородными.
При
![]() между
векторами
между
векторами
![]() и
и
![]() имеется фазовый сдвиг. Вектор
имеется фазовый сдвиг. Вектор
![]() опаздывает по фазе относительно вектора
опаздывает по фазе относительно вектора
![]() на угол
на угол
![]() .
В среде без потерь векторы
.
В среде без потерь векторы
![]() и
и
![]() изменяются синфазно. При изменении
изменяются синфазно. При изменении
![]() от нуля до бесконечности фазовый сдвиг
возрастает от нуля до
от нуля до бесконечности фазовый сдвиг
возрастает от нуля до
![]() .
На рис.14 и 15 показаны зависимости
мгновенных значений векторов
.
На рис.14 и 15 показаны зависимости
мгновенных значений векторов
![]() и
и
![]() от
времени
от
времени
![]() в
некоторой фиксированной точке пространства
(
в
некоторой фиксированной точке пространства
(![]() )
в
среде с
)
в
среде с
![]() и в среде без потерь. На рис.16 и 17 показаны
зависимости тех же величин от координаты
и в среде без потерь. На рис.16 и 17 показаны
зависимости тех же величин от координаты
![]() в некоторый фиксированный момент времени
в некоторый фиксированный момент времени
![]() для
случаев
для
случаев
![]() и
и
![]() .
.
Фазовая
скорость
![]() плоской волны находится так же, как в
случае сферической волны. Рассмотрим
перемещение
плоской волны находится так же, как в
случае сферической волны. Рассмотрим
перемещение
![]() ПРФ за время
ПРФ за время
![]() .
В
результате придем к равенству
.
В
результате придем к равенству
![]() ,
из
которого следует, что при
,
из
которого следует, что при
![]()
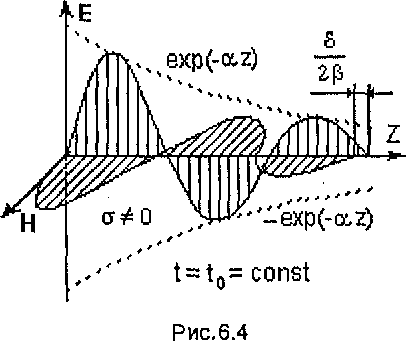
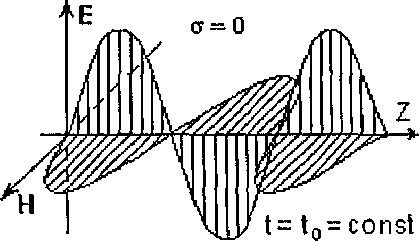
Рис.16
Рис.17
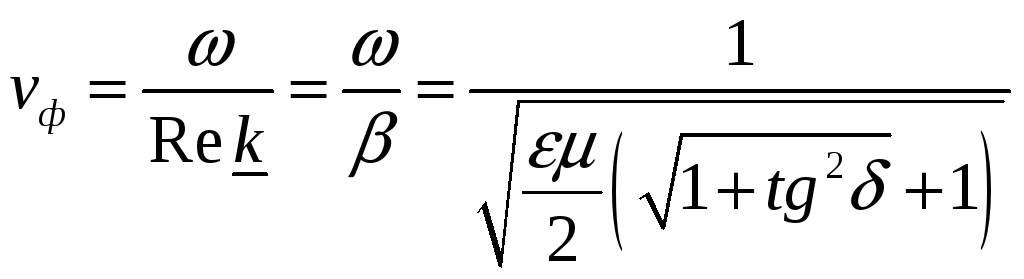 (19)
(19)
В
среде без потерь
![]() и
и
![]() ,
т.е. равна скорости света в среде с теми
же параметрами
,
т.е. равна скорости света в среде с теми
же параметрами
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() в
среде с потерями меньше
в
среде с потерями меньше
![]() в
среде без потерь с теми же
в
среде без потерь с теми же
![]() и
и
![]() .
.
Параметр
![]() ,
определяющий фазовую скорость, называют
коэффициентом
фазы.
При
,
определяющий фазовую скорость, называют
коэффициентом
фазы.
При
![]() фазовая скорость зависит от частоты
(
фазовая скорость зависит от частоты
(![]() ):
с увеличением последней она возрастает.
Предельное значение
):
с увеличением последней она возрастает.
Предельное значение
![]() при
при
![]() равно
равно
![]() .
Кроме того, величина
.
Кроме того, величина
![]() зависит от проводимости среды: при
одинаковой частоте она будет меньше в
среде с большей проводимостью.
зависит от проводимости среды: при
одинаковой частоте она будет меньше в
среде с большей проводимостью.
Длина
волны при
![]()
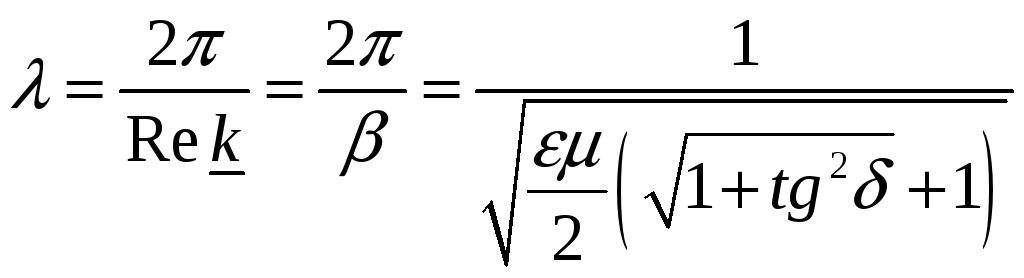 (20)
(20)
Она
меньше длины волны в среде без потерь
с теми же
![]() и
и
![]() .
Ее значение зависит от проводимости
среды. При
.
Ее значение зависит от проводимости
среды. При
![]() длина
волны
длина
волны
![]() ,
где
,
где
![]() .
.
Распространение
волны сопровождается переносом энергии.
При
![]() комплексный
вектор Пойнтинга
комплексный
вектор Пойнтинга
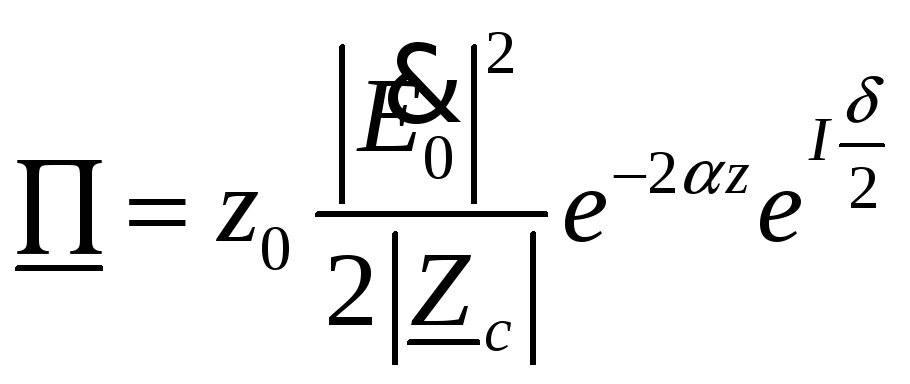 (21)
(21)
содержит
как действительную, так и мнимую часть.
Это означает, что имеется как активный,
так и реактивный поток энергии. Средняя
за период плотность потока энергии
экспоненциально убывает вдоль оси
![]() :
:
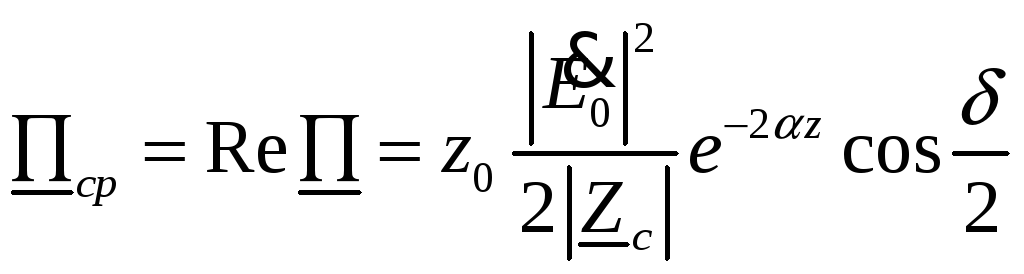 (22)
(22)
При
![]() комплексный вектор Пойнтинга является
чисто действительным и не зависит от
координат:
комплексный вектор Пойнтинга является
чисто действительным и не зависит от
координат:
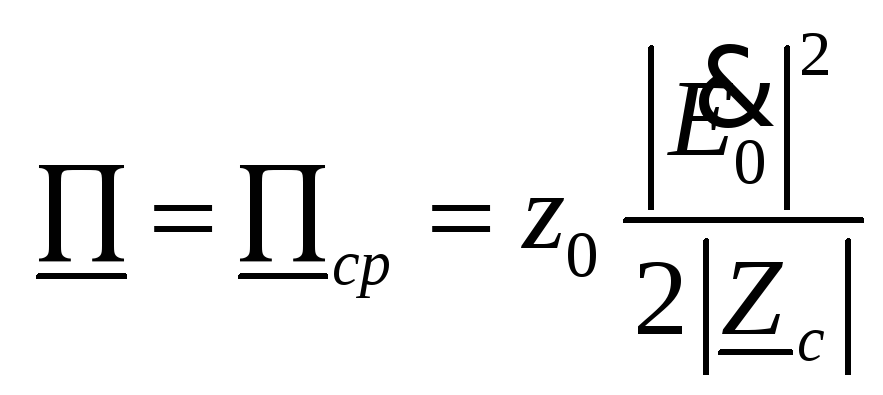 (23)
(23)
Как видно, в этом случае имеется только активный поток энергии.
Возникновение
реактивного потока энергии в среде с
![]() может
быть объяснено следующим образом. При
распространении электромагнитной волны
в среде возникают электрические токи
с плотностью
может
быть объяснено следующим образом. При
распространении электромагнитной волны
в среде возникают электрические токи
с плотностью
![]() ,
на поддержание которых расходуется
часть энергии волны. В свою очередь,
возникшие в среде электрические токи,
излучают .электромагнитное поле: создают
вторичную плоскую волну, которая
складывается с первичной, происходит
непрерывный обмен энергией между волной
и средой, что и приводит к возникновению
реактивного потока энергии.
,
на поддержание которых расходуется
часть энергии волны. В свою очередь,
возникшие в среде электрические токи,
излучают .электромагнитное поле: создают
вторичную плоскую волну, которая
складывается с первичной, происходит
непрерывный обмен энергией между волной
и средой, что и приводит к возникновению
реактивного потока энергии.
Скорость распространения энергии вычисляется по формуле и равна фазовой скорости:
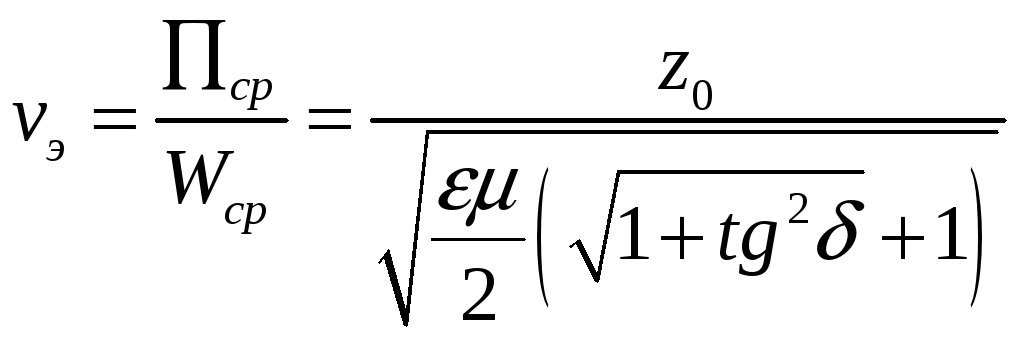 (24)
(24)
Как
видно, при
![]() скорость
распространения энергии зависит от
частоты. В среде без потерь
скорость
распространения энергии зависит от
частоты. В среде без потерь
![]() одинакова
при любой частоте.
одинакова
при любой частоте.
Характеристическое
сопротивление волны
![]() при
при
![]() также зависит от частоты. Модуль
также зависит от частоты. Модуль
![]() возрастает
с увеличением
возрастает
с увеличением
![]() .
Его
предельное значение при
.
Его
предельное значение при
![]() совпадает с характеристическим
сопротивлением волны, распространяющейся
в среде без потерь с теми же
совпадает с характеристическим
сопротивлением волны, распространяющейся
в среде без потерь с теми же
![]() и
и
![]() ,
т.е. равно
,
т.е. равно
![]() .
Аргумент характеристического сопротивления
.
Аргумент характеристического сопротивления
![]() изменяется
от
изменяется
от
![]() (при
(при
![]() )
до нуля (при
)
до нуля (при
![]() ).
).
Из
изложенного следует, что свойства
плоской волны, распространяющейся в
среде с проводимостью и в среде без
потерь, различны. Основное отличие
состоит в том, что в среде без потерь
параметры плоской волны (![]() и
др.) одинаковы при любых частотах, а в
среде с проводимостью они зависят от
частоты. Зависимость свойств волны от
частоты называется
дисперсией,
а соответствующие среды -
диспергирующими.
Отметим, что среда может быть диспергирующей
и при
и
др.) одинаковы при любых частотах, а в
среде с проводимостью они зависят от
частоты. Зависимость свойств волны от
частоты называется
дисперсией,
а соответствующие среды -
диспергирующими.
Отметим, что среда может быть диспергирующей
и при
![]() ,
если характеризующие ее параметры
,
если характеризующие ее параметры
![]() и
и
![]() зависят
от частоты.
зависят
от частоты.
В
общем случае вектор
![]() имеет две составляющие
имеет две составляющие
![]() и
и
![]() ,
между которыми возможен фазовый сдвиг.
При этом вектор
,
между которыми возможен фазовый сдвиг.
При этом вектор
![]() также будет иметь две составляющие
также будет иметь две составляющие
![]() и
и
![]() .
Если составляющие вектора
.
Если составляющие вектора
![]() по осям
по осям
![]() и
и
![]() (
(![]() и
и
![]() )
изменяются синфазно, то поворотом осей
координат
)
изменяются синфазно, то поворотом осей
координат
![]() и
и
![]() вокруг оси
вокруг оси
![]() этот
случай сводится к уже рассмотренному,
когда вектор
этот
случай сводится к уже рассмотренному,
когда вектор
![]() имеет одну составляющую. При наличии
между составляющими
имеет одну составляющую. При наличии
между составляющими
![]() и
и
![]() фазового сдвига, не равного
фазового сдвига, не равного
![]() ,
где
,
где
![]() - целое число, волна имеет некоторые
особенности, например при
- целое число, волна имеет некоторые
особенности, например при
![]() мгновенные
значения векторов
мгновенные
значения векторов
![]() не являются взаимно перпендикулярными.
Перечисленные выше остальные свойства
плоской волны имеют место и в этом
случае.
не являются взаимно перпендикулярными.
Перечисленные выше остальные свойства
плоской волны имеют место и в этом
случае.
