книги / Механика пластического деформирования трансверсально-изотропных композиционных сверхпроводниковых материалов

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

(1− σq1 )η2 (1+ 2a) + σq2 (1+ r2 ) − K

..pdf

Скачиваний:

Добавлен:

12.11.2023

Размер:

8.02 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2218 19 20 21 22 > Следующая >>>

В уравнении (5.20) перейдем к безразмерным переменным

σi = σxi / σsi ; x = x / L;

R = R / R0 = 1− x tg αв / R0 ; L = (R0 − R1 ) / tgαв.

С учетом соотношений (5.21) уравнение (5.20) примет вид

(dσi / d

) + σi a1i + σ1 a2i + σi−1 a3i + σi+1 a4i + a5i = 0 ,

ηi−1

; a4i = ηi+1

где a1i

= −

; a2

= 2a

/ ηi ; a3i

1− Rci2

ηi

ηi−1 − ηi+1

a5i

= A 1

−

; R

= 1− х

А; A = 1− R1 / R0 .

ηi

ηi (1− Rci )

(5.21)

(5.22)

;

Для n-слойной композиционной заготовки (i = 1, n) после подстановки соответствующих параметров получим систему неоднородных дифференциальных уравнений первого порядка с переменными коэффициентами, решение которой позволяет определить продольные напряжения в каждом слое. Таким образом, напряжения в слоях композиционной заготовки будут определяться комплексом пластических свойств слоев и геометрией очага деформации. Нормальные напряжения определяются из условий пластичности (5.12), а касательные напряжения на границах слоев из уравнения (5.14).

Определим напряжения в слоях наиболее распространенных типов слоистых композиционных заготовок.

5.2.1. Биметаллические заготовки

При использовании формулы (5.22) следует принять:

для оболочки: – σi	= σi−1 = σ1 ; σi+1 = σ2 ; ηi = ηi−1 = η1 = 1;		ci	=		c ;
		R			R
для сердечника: –	σi−1 = σ1 ; σi = σ2 ; σi+1 = 0 ; ηi−1 = η1 = 1 ;			ηi = η2 ;
ηi+1 = 0 .

Дифференциальные уравнения равновесия элементарных объемов компонентов заготовки имеют вид:

171

для оболочки

R(dσ1 / dx) + σ1 a1 + σ2 a2 + a3 = 0 ,

где а1 = − А(2 − А) ; а2 = − А η2 В ; а3 = − А(А− η2 В) ;

А= 2а+ (2 − Rc2 ) / (1− Rc2 ); B = Rc2 / (1− Rc2 );

η2 = σs 2 / σs1; Rс = Rc / R;

для сердечника

R dσ2 / dx + σ2 b1 + σ1b2 + b3 = 0 ,

где b1 = − A ; b2 = A η2 (1+ 2а) ; b3 = − A[1+ η2 (1+ 2a)].

Из уравнения (5.24) получим:

σ1 = −(1/ b2 ) (R dσ2 / dx + σ2 b1 + b3 ) ,

откуда

dσ1 / dx = −(1/ b1 )(− A dσ2 / dx + R d2σ2 / dx 2 + b1 dσ2 / dx ) .

(5.23)

(5.24)

(5.25)

(5.26)

Послеподстановки (5.25) и(5.26) в(5.33) ипреобразований имеем

2 d2σ2 / d

2 +

k1 dσ2 / d

+ k2 σ2 = k3 ,

(5.27)

где k1 = a1 + b1 +

; k2 = a1b1 − a2b2 ;

k3 = a3 b2 − a1 b3 .

Уравнение (5.27) является обобщенным дифференциальным

уравнением Эйлера [62] вида

(ax + b)n y(n) + a (ax + b)n−1 y(n−1)

+ ... + a

(ax + b) y′ + a y = f (x),

n−1

где а1 …. аn , а, b – постоянные.

Используя подстановку R = 1− x А = еt , получим

dσ2 / dx = − А e−t dσ2 / dt;

d2σ2 / dx 2 = A2 e−2t (d2σ2 / dt2 − dσ2 / dt ). (5.27 а)

172

Учитывая выражения (5.27, а), преобразуем уравнение (3.42):

d2σ2 / dt2 +					(5.28)
	k1 dσ2 / dt + k2 σ2 = k3 .

где k1 = − (k1 / A + 1); k2 = k2 / A2 ; k3 = k3 / A2 .

Решение уравнения (5.28) определяется суммой его частного решения и общего решения соответствующего однородного диффе-

ренциального уравнения:

d2σ2 / dt2 +

(5.29)

k1 dσ2 / dt + k2 σ2 = 0 .

Общее решение уравнения (5.28) зависит от вида корней его ха-

рактеристического уравнения, которое имеет вид

r2 +

(5.30)

k1 r + k2 = 0 ,

где r1,2 =

−

k1 ±

k12 − 4k2

Расчеты показывают, что для любого сочетания параметров во-

лочения ( αв ,

fn , η ,

) корни r1 и r2 характеристического уравнения

действительные. Тогда решение уравнения (5.29) имеет вид

σ2 = C1 er1 t + C2 er2 t + K

(5.30 а)

, где K

k3 / k2 .

Учитывая принятую ранее замену (

= еt ), запишем уравнение

(5.30 а)

σ2 = C1

r1 + C2

(5.31)

r2 + K

Константы C1 и C2 определяются из граничных условий:

σ1 x =0 = σq1 и σ2 x =0 = σq2 ,

где σq1 = σq1 / σs1 ; σq2 = σq2 / σs2 ; σq1 и σq2 – напряжения противонатяжения оболочки и сердечника соответственно.

Используя первое граничное условие и уравнения (5.25), (5.31), определим

173

Из уравнения (5.31) и второго граничного условия определим


С2 = σq2 − C1 − K		.	(5.33)

Из уравнения (5.26) определим продольные напряжения в оболочке

σ1 =

C1 r1

+ C2 r2

(1+ 2a) + 1

. (5.34)

+ K

+ η2

η2 (1+ 2a)

Формулы (5.31) и (5.34) неудобны в практическом применении, так как необходимо находить корни характеристического уравнения. Поэтому удобнее использовать приведенные ниже формулы (промежуточные выкладки, использованные при выводе формул (5.35)– (5.37), опущены вследствие громоздкости):

σ1 = η σ2 + ∆σ ;

σ2 = C1 + (σq2 − C1 − C2 )

2а + C2

2(B−1) ;

2(B−1)

− η σq2 )R

∆σ = (1− η)[B / (B − 1)] 1− R

+ (σq1

С1 = (1/ aη)[1+ 2а+ η − 2(1− η)(1+ 2а)B / (B − 1)];

− η) В− (σq1 − η σq2

)(B − 1)

(1+ 2а) (1

η (1+ a − B)(B − 1)

(5.35)

(5.36)

. (5.37)

5.2.2. Триметаллические заготовки

Для получения расчётных соотношений принимаем следующие допущения:

1. σs1 , σs2 , σs3 – сопротивления деформации наружной оболочки,

промежуточной оболочки и сердечника соответственно; 2. Награницахразделаслоев действуют нормальные напряжения:

σncp1	=	σn1 + σn2	; σncp2	=	σn2 + σn3	,	(5.38)

	2			2

где σn1 , σn2 , σn3 – нормальные напряжения в сечении наружной оболочки, промежуточной оболочки и сердечника соответственно.

174

3. Соотношение наружных радиусов заготовки R , промежуточной оболочки Rc1 и сердечника Rc 2 в процессе волочения остается постоянным:

R1 = Rc1 / R = const ; R2 = Rc2 / R = const ; R3 = Rc2 / Rс1 = const .

4. Углынаклонамежслойных границопределяются выражениями:

tg α1 = R1 tg αв ; tg α2 = R2 tg αв ,

где α1 и α2 – угол наклона границы между наружной и промежу-

точной оболочкой и сердечником соответственно.

5. Касательные напряжения на границах слоев определяются:

– на границе наружной и промежуточной оболочек:

τм1 = fn σn1

(5.39)

R1 ,

– на границе промежуточной оболочки и сердечника:

τм2

= fn σn2

2 .

(5.40)

Используя (5.40), получим дифференциальные уравнения для

слоев:

для наружной оболочки ( ηi−1 = 1)

dσ1 / d

+ a11 σ1 + a21 σ2 + a31 = 0 ,

(5.41)

где

= R / R0 = 1−

;

= 1− R1 / R0 ;

= x / L

( 0 ≤ х ≤ 1);

а11 = −С1

; а21 = −η1 В1

; а31 = −С2

; L – длина очага деформа-

ции;

для промежуточной оболочки ( ηi−1 = 1)

dσ2 / d

+ а12 σ2 + а22 σ1 + а32 σ3 + а42 = 0 ,

(5.42)

где а12

= −

; а22 = −

C3 / η1 ; а32 = −

В2 η2 / η1 ; а42 = −

C4 / η1 ;

для сердечника ( ηi+1 = 0 )

dσ3 / d

+ а13 σ3 + а23 σ1 + а33 σ3 + а43 = 0 ,

(5.43)

где а13 = −

; а23 = 2a

/ η2 ;

а33 =

η1 / η2 ;

а43 = −

C5 / η2 .

175

C1 = 2 − A1 ; C2 = A1 − η1 B1 ; C4 = η1 − η2 B2 − C3 ;

C5 = 2a + η1 + η2 ; η1 = σs 2 / σs1 ; η2 = σs3 / σs1 ; a = fn / tgαв ;

1+ (1+ 2a

)(1−

A =

R12 )

; С = −

1+ 2а(1− R32 )

;

B =

R12

; B

1− R12

1− R32

− R12

1− R32

Из уравнения (5.42) определим:

σ3 = −

(

dσ2

+ а12 σ2 + а22 σ1 + а42 ) .

(5.44)

а32

Из уравнения (5.44) после дифференцирования получим

dσ3

d2σ2

dσ2

dσ1

= −

+ (а12 − A)

+ а22

(5.45)

а32

Из уравнения (5.41) определим:

σ2 = −

dσ1

+ a11

σ1 + a31 ;

(5.46)

a21

dσ2

d2σ1

dσ1

= −

+ (a11 − A)

;

(5.47)

a21

d2σ2

d3σ1

d2σ1

= −

+ (a11

− 2A)

(5.48)

a21

Подставляя уравнения(5.44)–(5.48) вуравнение(5.43), определим

d3σ1

+ c

d2σ1

+ c

dσ1

+ c

σ = c ,

(5.49)

где

c1 = a11 + а12 + а13 − 3

;

= (a11 −

)(а12 + а13 −

) − a21а22 + а12а13 −

− а32а33 ;

c3 = a11 (а12а13 − а32а33 ) − a21 (а22а13 − а32а23 ) ; с4 = a21 (а42а13 − а32а43 ) − a31 (а12а13 − а32а33 ) .

176

Приведем уравнение (5.49) к линейному дифференциальному уравнению 3-го порядка с постоянными коэффициентами:

d3σ1

d2σ1

dσ1

σ =

(5.50)

dt3

dt2

k1 = −с1 / A − 3 ; k2 = 2 − c1 / A + c2 / A2 ; k3 = −c3 / A3 ; k4 = −c4 / A3 .

Решение уравнения (5.50) равно сумме общего решения и1 (t) и

частного решения u2 (t) , которое имеет вид

u2 (t) =

k4 / k3 = c4 / c3 = K

(5.51)

Общее решение уравнения (5.50) получим из решения однород-

ного дифференциального уравнения:

d3σ1 / dt3 +

(5.52)

k1 d2σ1 / dt2 + k2 dσ1 / dt + k3 σ1 = 0 .

Запишем характеристическое уравнение для уравнения (5.52)

r3 +

(5.53)

k1 r2 + k2 r + k3 = 0 ,

Подстановкой r = y −

к не-

k1 / 3 преобразуем уравнение (5.53)

полному виду

y3 + p y2 + q = 0 ,

(5.54)

где p = −(

k12 / 3) + k2 ; q = 2(k1 / 3)3 − (k1 k2 / 2) + k3 .

Решение неполного уравнения находим в виде

y1 = A + B ; y2,3 = −

A + B

± i

A − B

3 ;

A = 3 −q / 2 + Q ; B = 3 −q / 2 − Q ; Q = ( p / 3)3 + (q / 2)2 .

Вид решения уравнения (5.52) и корней характеристического уравнения зависит от знака величины Q: если Q < 0 , то корни урав-

нения (5.53) действительные; если Q > 0 , то один корень уравнения (5.53) действительный, а два – комплексные.

177

Исследование влияния параметров процесса волочения на знак величин р и Q показывает, что практически для всех реализуемых параметров процесса волочения и сочетаний геометрических соотношений и пластических свойств слоев заготовки Q > 0 , поэтому

решение уравнения (5.52) имеет вид

σ1 (t) = C1 er t сos(s t) + C

2 er t sin(s t) + C

3 er3 t .

(5.55)

где r1 = r + i s ;

r2 = r − i s ; r3 – корни характеристического уравнения;

r = (r1 + r2 ) / 2 ; s = (r1 − r2 )i / 2 .

Решение

уравнения (5.55) с учетом подстановки et

= 1−

имеет вид

σ1 =

r [C1 сos(s t) + C2 sin(s t)] + C3

r3 + K

(5.56)

Используя уравнения (5.44), (5.46), (5.56) и граничные условия

σ1

х=0 = σq1 , σ2

х=0 = σq2 , σ3

х=0 = σq3 ,

получим систему линейных алгебраических уравнений

С1 + С3 = σq1

− K

;

+ σq2 a21 + a31

C1 (A r − a11 ) + C2 A s + C3 (A r3 − a11 ) = a11 K

;

C1[A2 (r2 − r − s2 ) − A r(a11 + а12 − A) + a11 а12 − a21 а22 ] +

,(5.57)

2 s[A2 (2 r − 1) − A(a11 + а12 − A)] +

+C3[A

r3 (r3

− 1) − A r3 (a11 + а12 − A) + a11 а12 − a21 а22 =

= σq3 a21 а32 − a31 а12 + a21 а42 − K (a11 а12 − a21 а22 );

решение которой позволяет определить неизвестные константы С1 , С2 и С3 . Напряжения σ2 и σ3 определяются изуравнений(5.46) и(5.44).

Соотношения для расчёта продольных напряжений в слоях триметаллической композиционной заготовки включают следующие параметры: σS1 , αв , fn , λ , R1 , R2 , η1 , η2 , σq . Поскольку возмож-

178

ное число сочетаний численных значений этих параметров велико, то влияние каждого из них на процесс волочения необходимо оценивать для конкретной конструкции композиционной заготовки.

Полученная модель позволяет учесть влияние упрочнения металла и формы канала волочильного инструмента на величину напряжений в слоях заготовки. При достаточной дискретизации исследуемой области модель позволяет показать влияние неравномерного упрочнения слоев при волочении монометаллической заготовки или влияние так называемого «положительного» или «отрицательного» градиента механических свойств при волочении слоистой заготовки, когда пластические характеристики слоев увеличиваются или, наоборот, уменьшаются от поверхности к центру заготовки.

5.3. Влияние параметров процесса волочения на величину напряжений в слоях композиционной заготовки

Биметаллические заготовки

Используя соотношения, полученные в предыдущем разделе, проанализируем влияние основных параметров, характеризующих процесс волочения, на величину продольных напряжений. На рис. 5.8–5.17 σх1 и σх2 – продольные напряжения в оболочке и сердечнике. Напряжение волочения заготовки вычислялось по формуле

σ		= σ (1−		2 ) + σ			2 .	(5.58)
	вол		R		2	R
		1	c			c

Распределение напряжений по длине очага деформации

На рис. 5.8 приведены результаты расчета напряжений вдоль очага деформации для набора некоторых стандартных параметров процесса волочения (оболочка пластичнее сердечника): σs1 = 400 МПа; η = 0,3;

fn = 0,05; α В = 8 0; R0 = 1 мм; λ = 1,235; σq = 0,1σs (k = 0,1).

Из рисунка видно, что для принятых параметров продольные напряжения нелинейно возрастают и на выходе из очага деформации достигают величин: 0,57 σS для оболочки и 0,63 σS для сердечника.

179

σx1 / σs2

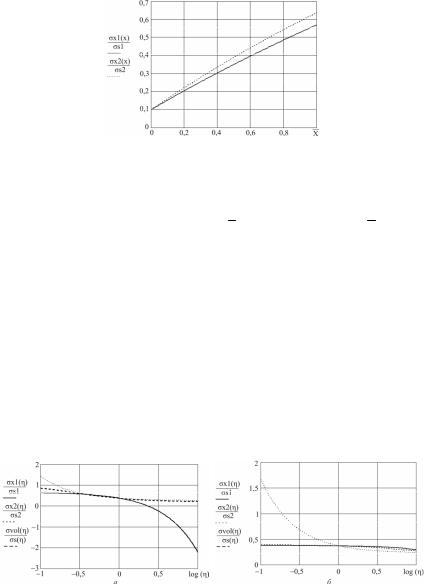
Рис. 5.8. Распределение продольных напряжений в очаге деформации

Влияние пластической неоднородности

Результаты расчета продольных напряжений на выходе из очага деформации приведенынарис. 5.9, а( Rс = 0,9 ) ирис. 5.9, б( Rс = 0,3).

При волочении заготовки с тонкой оболочкой рост прочностной неоднородности ведет к уменьшению относительных продольных напряжений в оболочке и в сердечнике σx2 / σs2 (см.

рис. 5.9, а). При этом напряжения в сердечнике во всем диапазоне изменения η остаются растягивающими.

Если оболочка пластичнее, чем сердечник ( η > 1), то напряжения

в оболочке сжимающие. В тонкой более прочной оболочке напряжения растягивающие и при уменьшении η .

С уменьшением относительного радиуса сердечника и с ростом прочностной неоднородности растягивающие напряжения в сердечнике возрастают, а в оболочке уменьшаются (рис. 5.9, б).

Рис. 5.9. Влияние коэффициента пластической неоднородности

на величину продольных напряжений: а –

= 0,9; f

= 0,05 ; α

= 80

; k = 0,1;

б –

= 0,3; f

= 0,05 ; α

= 80 ; k = 0,1

180

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2218 19 20 21 22 > Следующая >>>

Соседние файлы в папке книги

#
13.11.202324.83 Mб9Механика материалов. Методы и средства экспериментальных исследований.pdf
#
12.11.202320.8 Mб2Механика мёрзлых грунтов (общая и прикладная)..pdf
#
19.11.202330.62 Mб2Механика мерзлых грунтов и принципы строительства нефтегазовых объектов в условиях севера..pdf
#
13.11.202323.18 Mб0Механика многослойных конструкций..pdf
#
12.11.202315.25 Mб0Механика насыщенных пористых сред..pdf
#
12.11.20238.02 Mб2Механика пластического деформирования трансверсально-изотропных композиционных сверхпроводниковых материалов..pdf
#
12.11.202312.72 Mб3Механика подземных сооружений в примерах и задачах..pdf
#
12.11.20239.74 Mб19Механика промышленных роботов и манипуляторов с электроприводом..pdf
#
12.11.20236.09 Mб3Механика разрушения вязко-упругих тел..pdf
#
19.11.202334.67 Mб0Механика разрушения композитных материалов при сжатии..pdf
#
19.11.202326.62 Mб0Механика разрушения. Быстрое разрушение, остановка трещин.pdf