книги / Сборник задач по общей физике

Р е ш е н и е.

Показание U1 вольтметра, подключенного к точкам А и В (рисунок), определяется по формуле

U1 = I1R1, (1)

где I1 – сила тока в неразветвленной части цепи; R1 – сопротивление параллельно соединенных вольтметра и половины потенциометра.

Силу тока I1 найдем по закону Ома для всей цепи:

где R – сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

Если подставить значения I1 и R1 в формулу (1), то можно определить показание вольтметра: U1 = 1,03 · 45,5 В = 46,9 В.

Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I2 на половину сопро-

101

Подставляя в эту формулу числовые значения, получим

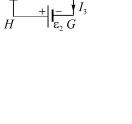
№ 5. Электрическая цепь состоит из двух гальванических элементов, трех сопротивлений и гальванометра. В этой цепи R1 = 100 Ом, R2 = 50 Ом, R3 = 20 Ом, ЭДС элемента ε1 = 2 В. Гальванометр регистрирует ток I3 = 50 мА, идущий в направлении, указанном стрелкой.

Определить ЭДС ε2 второго элемента. Сопротивлением гальванометра и внутренним сопротивлением элементов пренебречь.

Р е ш е н и е.

Выберем направления токов, как они показаны на рисунке, и условимся обходить

контуры по часовой стрелке.

По первому правилу Кирхгофа для узла F имеем

По второму правилу Кирхгофа имеем для контура АВСDFА

После подстановки числовых значений в формулы (1), (2) и (3) получим

I1 – I2 = 0,05,

50I1 + 25I2 = 1,

100I1 + 0,05 · 20 = ε2.

Перенеся в этих уравнениях неизвестные величины в левые части, а известные – в правые, получим следующую систему уравнений:

102

I1 – I2 = 0,05, 50I1 + 25I2 = 1, 100I1 – ε2 = –1.

Эту систему с тремя неизвестными можно решить обычными приемами алгебры, но, так как по условию задачи требуется определить только одно неизвестное ε2 из трех, воспользуемся методом

ε2 = –300/(–75) = 4 В.

№ 6. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени t = 2 с по линейному закону от I0 = 0 до I2 = 6 А. Определить теплоту Q, выделившуюся в этом проводнике за вторую секунду.

Р е ш е н и е.

Закон Джоуля–Ленца в виде Q = I2Rt справедлив только для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

где k – коэффициент пропорциональности, численно равный приращению силы тока в единицу времени, т.е.

103

Для определения теплоты, выделившейся за конечный промежуток времени t, выражение (3) следует проинтегрировать в пределах от t1 до t2:

При определении теплоты Q, выделившейся за вторую секунду, пределы интегрирования t1 = 1 с, t2 = 2 с, тогда

Q 13 32 20 8 1 420 Дж.

3.3. Электромагнетизм

Задачи по теме электромагнетизма можно разделить на две основные группы: задачи о силовом действии однородного магнитного поля на проводники с током и заряженные частицы и задачи на закон электромагнитной индукции.

Задачи расчетного характера о силах, действующих на проводники с током в однородном магнитном поле, удобно решать по следующей схеме:

1. Сделать схематический чертеж, на котором указать контур (проводник) с током и направление линий магнитной индукции

поля. Обозначить углы между направлением вектора B и отдельными элементами контура, если последний состоит из нескольких проводников.

2. Используя правило левой руки, определить направление сил Ампера, действующих на каждый элемент контура, и нанести их на чертеж.

104

3. Если в задаче рассматривается равновесие проводника, то, помимо сил Ампера, нужно указать все остальные силы, приложенные к проводнику, и записать условие его равновесия.

Решение задач на движение заряженных частиц в электро-

магнитных полях в большинстве случаев основано на составлении основного уравнения динамики материальной точки с учетом сил, действующих на заряженную частицу со стороны магнитного и электрического полей. При нахождении направления силы Лоренца следует обратить особое внимание на знак заряда частицы. Указав силы, нужно попытаться определить вид траектории частицы. Иногда это удается сделать просто, иногда это представляет основное содержание задачи.

При решении задач на закон электромагнитной индукции следует придерживаться следующей последовательности действий:

1. Анализируя условие задачи, необходимо прежде всего установить причины изменения магнитного потока, сцепленного с контуром, и определить, какая из величин – В, S или – изменяется с течением времени. После этого нужно записать закон Фарадея. Если в задаче рассматривается поступательное движение прямого проводника, то ЭДС индукции определяют по формуле= Blvsin (l – длина проводника; v – его скорость), вытекающей из закона электромагнитной индукции.

2. Выражение для Ф представить в развернутом виде. Для этого выбирают два момента времени и для каждого из них определяют потоки Ф1 и Ф2, связанные с данным контуром. Изменение магнитного потока будет или Ф = (В2 – В1)Scos , если изменяется индукция магнитного поля, или Ф = ВS(cos 2 – cos 1) при изменении положения рамки, или Ф = В Scos , где S – изменение площади контура, описанного в пространстве движущимся проводником.

3. Подставить выражение для Ф в исходную формулу закона Фарадея и, записав дополнительные условия, решить совместно полученные уравнения относительно искомой величины.

105

Основные формулы

1. Связь магнитной индукции B с напряженностью H маг-

нитного поля

B μμ0 H ,

где – магнитная проницаемость однородной среды; 0 – магнит-

ная постоянная. В вакууме = 1, и магнитная индукция в вакууме

B μ0 H.

элемента проводника к точке, в которой определяется магнитная индукция; – угол между радиус-вектором и направлением тока

вэлементе провода.

3.Принцип суперпозиции магнитных полей

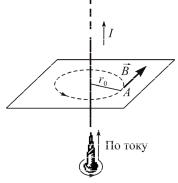
Направление вектора магнитной

индукции B поля, создаваемого прямым током, определяется по правилу буравчика (правого винта). Для этого проводим магнитную силовую линию (штриховая линия на рисунке) и по касательной к ней в интересующей нас точке проводим вектор

B . Вектор магнитной индукции B в точке А направлен перпендикулярно плоскости чертежа от нас.

106

4. Магнитная индукция в центре кругового тока

B μμ2R0 I ,

где R – радиус кругового витка.

Магнитная индукция на оси кругового тока

где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.

Магнитная индукция поля, создаваемого отрезком провода с током (вывод этой формулы в примере № 1),

B μμ0 I cos 1 cos 2 . 4π r0

Магнитная индукция поля, создаваемого бесконечно длинным прямолинейным проводником с током,

B μμ0 I , 2πr0

где r0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.

Магнитная индукция поля бесконечно длинного соленоида

B = 0nI,

где n – отношение числа витков соленоида N к его длине l.

5. Сила, действующая на элемент провода с током в магнитном поле (закон Ампера),

dF I dl B ,

где dl – вектор, равный по модулю длине участка провода и совпадающий по направлению с током; – угол между направлением тока в проводе и вектором магнитной индукции B.

107

Для однородного магнитного поля и прямого отрезка провода получим

FIBlsin .

6.Магнитный момент плоского контура с током

pm ISn,

где n – единичный вектор нормали (положительной) к плоскости контура; I – сила тока, протекающего по контуру; S – площадь контура.

7. Механический вращающий момент, действующий на контур с током, помещенный в однородное магнитное поле,

где v – скорость заряженной частицы; – угол между векторами v и B.

Если частица находится одновременно в электрическом и магнитном полях, то на нее действует сила

FqE q v B .

9.Магнитный поток (через поверхность S):

а) в случае однородного магнитного поля и плоской поверхности

Ф = BScos , или Ф = BnS,

где S – площадь контура; – угол между нормалью к плоскости контура и вектором магнитной индукции;

б) в случае неоднородного поля и произвольной поверхности

BdS BndS

S S

(интегрирование ведется по всей поверхности).

108

Потокосцепление (полный поток) = NФ.

Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

10.Работа по перемещению замкнутого контура с током в магнитном поле δA = IdФ, или А = I Ф.

11.Основной закон электромагнитной индукции (закон Фара-

дея – Максвелла) εi d N d . dt dt

Разность потенциалов на концах проводника, движущегося со скоростью v в магнитном поле, U = Blvsin , где l – длина прово-

да; – угол между векторами v и B.

Заряд, протекающий по замкнутому контуру при изменении магнитного потока, пронизывающего этот контур, dq dRФ , или

dq N dR dR , где R – сопротивление контура.

12. Индуктивность контура L = Ф/I.

Индуктивность соленоида L = 0n2lS, где n – отношение числа витков соленоида к его длине; l – длина соленоида, S – площадь его поперечного сечения.

13. ЭДС самоиндукции

εsi L ddIt .

14.Мгновенное значение силы тока в цепи, обладающей сопротивлением R и индуктивностью L:

а) I Rε 1 e Rt / L – при замыкании цепи, где – ЭДС источ-

ника тока; t – время, прошедшее после замыкания цепи;

б) I I0e Rt / L – при размыкании цепи, где I0 – сила тока в цепи при t = 0; t – время, прошедшее с момента размыкания цепи.

15. Энергия магнитного поля соленоида W = LI22 .

109

Объемная плотность энергии магнитного поля (отношение энергии поля к его объему)

Примеры решения задач

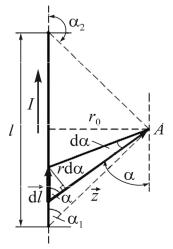
№ 1. По отрезку прямого провода длиной l = 80 см течет ток

I = 50 А. Определить магнитную индукцию B поля, создаваемого этим током в точке А, равноудаленной от концов отрезка провода

инаходящейся на расстоянии r0 = 30 см от его середины.

Ре ш е н и е.

Для решения задачи воспользу-

и принципом суперпозиции магнитных полей

где символ l означает, что интегрирование распространяется на всю

длину провода; dB – магнитная индукция, создаваемая элементом тока

Idl в точке, определяемой радиусвектором r; 0 – магнитная постоянная; – магнитная проницаемость среды, в которой находится провод (в нашем случае = 1).

Векторы dB от различных элементов тока сонаправлены, поэтому выражения (1), (2) можно переписать в скалярной форме:

110