
книги / Надёжность технических систем и техногенный риск. Структурно-энергетическая теория отказов
.pdfОднако на практике такие кривые не встречаются. Можно указать различные причины, вызывающие рассеяние значений энергии разрушения, главными из которых являются:
–неоднородность структуры материалов элементов;
–неравномерность поглощения энергии структурными единицами материалов элементов;
–случайный характер взаимодействия энергии со структурными единицами материалов элементов (случайный характер физикохимических процессов, ответственных за развитие отказа).
Неоднородность характерна для всех реальных материалов. Она может быть закономерной или случайной в зависимости от того, создается ли она при закономерном изменении средних характеристик среды или в результате локальных случайных отклонений характеристик материала от их средних значений на субмикроскопическом, микроскопическом или макроскопическом уровнях агрегации материала.
Случайная неоднородность на субмикроскопическом уровне обычно связана с наличием в материале элементарных структурных дефектов, таких как вакансии, дефекты упаковки и дислокации.
Вмикромасштабах она связана с размером, ориентацией или физическими свойствами структурных единиц материала микроскопического размера, таких как кристаллы или частицы. На макроскопическом уровне она связана со случайными колебаниями макроскопических свойств, наблюдаемых локально на единичном образце или в целом на образцах номинально идентичных (таких свойств, как механические, электрические, магнитные и т.д.). Очевидно, макроскопическая неоднородность, выраженная в форме статистической дисперсии наблюдаемых характеристик, является результатом как субмикроскопических дефектов, так и микроскопических случайных неоднородностей в материале. Такая неоднородность структуры материала может привести к рассеянию энергии разрушения; тогда вместо кривой функции распределения энергии разрушения ступенчатой формы будут получаться кривые S-образной формы (см. рис. 5.1, кривая 2).
81
Наряду с этим на форму кривой функции распределения энергии разрушения может влиять микроскопическое пространственное распределение энергии по объему материала элемента. Если в материале элемента чувствительны только малые участки, например дефектные структуры, то при данной величине энергетического воздействия величина энергии, фактически поглощенная этими дефектными структурами или вблизи них, будет колебаться в широких пределах. Следовательно, разрушение (отказ) не может наступать во всех элементах при некоторой пороговой величине энергетического воздействия. Таким образом, пространственные флуктуации поглощенной энергии могут увеличивать дисперсию энергии разрушения.
Наряду с этими аспектами необходимо принимать во внимание
итретий фактор – случайный характер взаимодействия энергии со структурными единицами материалов элементов. Даже если отвлечься от неоднородности структуры материалов и неравномерности распределения поглощенной энергии, кривая функции распределения энергии разрушения не обязательно должна иметь ступенчатую форму. Объясняется это тем, что при известных исходных условиях поведение элемента в значительной степени неопределенно. Здесь имеется в виду не столько принципиальная неопределенность квантово-механических процессов, которая, пожалуй, и может быть ответственной за флуктуации физико-химических процессов в материалах элементов, сколько то, что взаимодействие многочисленных компонентов структуры материалов друг с другом
ис факторами, обусловленными средой, принципиально не допускает ничего иного, кроме вероятностных высказываний о процессах в материалах элементов.
5.2. Анализ влияния вариации размеров и числа чувствительных структур на надежность элементов
Структурно-энергетические модели отказов позволяют легко оценить влияние структурных факторов (количества и размеров чувствительных структур материалов) на форму кривой функции распределения энергии разрушения, а следовательно, на надежность
82
элементов, и на этой основе разработать конкретные рекомендации по технологическому обеспечению заданного уровня надежности и качества элементов.
Из рассмотрения структурно-энергетических моделей отказов видно, что на надежность элементов может оказывать влияние как вариация размеров, так и вариация количества чувствительных структур в материале элемента.
Сначала рассмотрим влияние вариации размеров чувствительных структур ϑ на надежность элементов при n0 = 1. Из модели отказов (4.14) следует, что при n0 = 1 зависимость вероятности отказа от величины энергетического воздействия будет простой экспонентой
q(ε) = 1− exp(−ϑε) .
Построим кривые функции распределения энергии разрушения для следующих четырех случаев (рис. 5.2):
1) n0 = 1, ϑ = const, т.е. функция q(ε) задается уравнением q(ε) = 1 – exp(–ϑ ε);
2) n0 = 1, ϑ ≠ const, при этом предполагаем, что 50 % элементов совокупности имеет на 20 % меньшую по размерам чувствительную структуру, чем остальные, т.е. функция q(ε) задается выражением
q(ε) = 1 – 0,5exp(–ϑ ε) – 0,5exp(–0,8ϑ ε);
3) n0 = 1, ϑ ≠ const, 50 % элементов имеют чувствительные структуры размером ϑ , а 50 % – размером 0,1ϑ , т.е. функция q(ε) задается уравнением
q(ε) = 1 – 0,5exp(–ϑ ε) – 0,5exp(–0,1ϑ ε);
4) n0 = 1, ϑ ≠ const, 3 % элементов имеют чувствительную структуру размером 0,2ϑ ; 10 % – 0,3ϑ ; 10 % – 0,4ϑ ; 50 % – 0,5ϑ ;
10 % – 0,6ϑ ; 10 % – 0,7ϑ ; 3 % – 0,8ϑ ; 2 % – 0,9ϑ ; 2 % – 0,1ϑ , т.е.
функция распределения энергии разрушения строится поуравнению q(ε) = 1 – 0,02[exp(–0,1ϑ ε) + exp(–0,9ϑ ε)] –
–0,1[exp(–0,3ϑ ε) + exp(–0,4ϑ ε) + exp(–0,6ϑ ε) + exp(–0,7ϑ ε)]–
–0,03[exp(–0,2ϑ ε) + exp(–0,8ϑ ε) – 0,5exp(–0,5ϑ ε)].
83
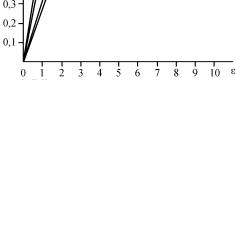
Рис. 5.2. Влияние вариации размеров чувствительных структур на надежность элементов при n0 = 1
Как видно из рис. 5.2, допущение о том, что 50 % элементов имеют чувствительную структуру размером ϑ и 50 % – размером 0,8ϑ (кривая 2), мало сказалось на отклонении кривой 2 от кривой 1, т.е. мало сказалось на изменении надежности элементов. Отклонения более существенны для кривой 4, при расчете которой допускалась близкая к реальной вариация размеров чувствительных структур в партии элементов, и особенно большие отклонения возникают при допущении, что половина элементов имеет чувствительную структуру в 10 раз меньшую (кривая 3).
Что касается кривых функции распределения энергии разрушения для n0 > 1, то вариация размеров чувствительных структур, как это следует из модели (4.14), также вызывает большие искажения форм соответствующих кривых. Это видно из рис. 5.3, на котором
– кривая 1 построена для случая n0 = 1, ϑ = const по уравнению q(ε) = 1 – exp(–ϑ ε);
– кривая 2 – для случая n0 = 2, ϑ = const по уравнению q(ε) = 1 – exp(–ϑ ε) (1 + ϑ ε);
84
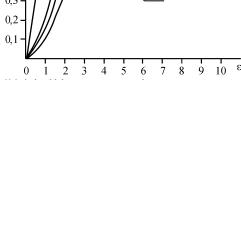
– кривая 3 – для случая n0 = 3, ϑ = const по уравнению
q(ε) = 1− |
|
(ϑε) |
2 |
exp(−ϑε) ; |
1+ ϑε + |
|
|||
|
|
2! |
|
|
|
|
|
|
|
– кривая 4 – для случая n0 = 3, ϑ ≠ |
const (50 % элементов имеют |
|||
чувствительную структуру размером ϑ , а остальные – 2ϑ ) по уравнению
q(ε) = 1− |
1+ ϑε + |
(ϑε) 2 |
|
0,5exp(−ϑε) − |
||
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
− 0,5 |
|
+ 2ϑε + |
(ϑε)2 |
2 |
|
|
1 |
|
exp(− ϑε)2 . |
||||
Рис. 5.3. Влияние вариации размеров чувствительных структур на надежность элементов при n0 > 1
Из рис. 5.3 видно, что имеется значительное расхождение между кривыми 3 и 4, что свидетельствует о сильном влиянии вариации размеров чувствительных структур на форму функции q(ε). В связи с этим важно заметить, что расхождения, обусловленные вариацией размеров чувствительных структур, приводят к деформации кривой функции q(ε) таким образом, что она по форме приближается к кривой, построенной для n0 = 2, ϑ = const. Следовательно, вариация
85
размеров чувствительных структур в партии элементов приводит к уменьшению среднего числа квазичастиц, необходимых для возникновения отказа.
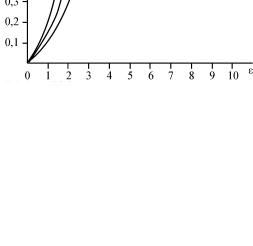
В качестве примера оценки влияния вариации числа чувствительных структур на надежность элементов рассмотрим случай, когда энергетическому воздействию подвергается совокупность элементов, у 50 % которых для возникновения отказа достаточно поглощения трех квазичастиц одной чувствительной структурой, а у остальных 50 % требуется поглощение трех квазичастиц каждой из двух чувствительных структур. Соответствующая этому случаю кривая 3, представленная на рис. 5.4 и рассчитанная по уравнению
q(ε) = 1− 1+ ϑε + |
(ϑε) |
|
2 |
0,5exp(−ϑε) − |
||
|
|
2! |
|
|
|
|
|
|
|
|
|
||
|
|
(ϑε) |
2 |
|
|
2 |
|
|
|
|
|
|
|
− 0,5 1 |
+ ϑε + |
2! |
|
exp(−ϑε) |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5.4. Влияние вариации числа чувствительных структур на надежность элементов n0 = 3
86
лежит между кривыми 1 и 2 с параметрами n0 = 2, m = 1 и n0 = 3, m = = 1, ближе к первой из них, т.е. наблюдается картина, аналогичная варьированию размеров чувствительных структур.
Таким образом, как вариация размеров, так и вариация числа чувствительных структур, приходящихся на каждый элемент совокупности, приводит к уменьшению среднего числа квазичастиц, необходимых для возникновения отказа. Этот факт, установленный чисто расчетным путем и находящий подтверждение на практике, имеет важное значение в теории надежности, поэтому в целях общности выводов дадим ему теоретическое обоснование в рамках структурно-энергетической концепции отказов.
5.3. Относительная крутизна функции распределения энергии разрушения
Основными характеристиками функции распределения энергии разрушения (см. рис. 5.1) являются ее первые два момента. Первый момент равен среднему значению энергии разрушения
m1 = ε = |
∞∫ε f ε( )dε . |
(5.1) |
|
|
0 |
|
|
Второй момент |
|
|
|
m2 = ∞∫ε 2 |
f (ε |
)dε |
(5.2) |
0 |
|
|
|
определяет совместно с первым моментом дисперсию |
|
||
σ ε2= |
m1− |
m12 . |
(5.3) |
Вместо дисперсии в качестве характеристики функции распределения энергии разрушения введем понятие относительной крутизны S, под которой будем понимать отношение
S = |
ε 2 |
, |
(5.4) |
|
σ ε2 |
||||
|
|
|
||
|
|
|
87 |
где ε – среднеезначениеэнергииразрушенияоднотипныхэлементов; σ ε2 – дисперсия энергии разрушения.
Относительная крутизна S определяет характер зависимости вероятности отказа от величины энергетического воздействия: чем круче кривая, т.е. чем больше она приближается к ступенчатой форме, тем больше величина S. Легко видеть, что для экспоненциальной кривой S равна 1, в то время как для отличной от экспоненциальной кривой она будет больше 1. Для чисто ступенчатой формы следует считать, что значение S = ∞ . Все случайные факторы, которые оказывают влияние на функцию распределения энергии разрушения, уменьшают значение S. Следовательно, по величине S можно судить в общих чертах о преобладающем влиянии той или иной причины разрушения (отказа) элемента.
Для выяснения физического смысла введенного понятия «относительная крутизна» кривой распределения выведем следующее важное соотношение. Пусть распределение вероятности отказа q(ε) есть выпуклая линейная комбинация распределений qi(ε):
|
|
K |
|
|
|
q(ε )= ∑Ci qi(ε ), |
(5.5) |
|
|
i =1 |
|
K |
|
|
|
где ∑Ci |
=1 и Ci ≥ 0. |
|
|
i=1 |
|
|
|
Пусть ε |
и σ ε2 являются средним значением и дисперсией для |
||
q(ε), а ε i |
и σ |
i2 – средним значением и дисперсией для qi(ε). Эти ве- |
|
личины должны существовать и не равняться нулю. Тогда справедливо следующее утверждение.
Утверждение 1. Если функция распределения q(ε) есть выпуклая линейная комбинация распределений qi(ε), то относительная крутизна S линейной комбинации различных функций распределения меньше или равна соответствующей линейной комбинации величин Si отдельных функций распределения, т.е.
88
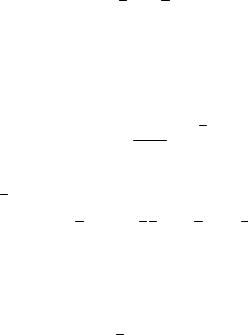
S = ε |
2 |
|
≤ |
∑Ci |
ε i2 = |
||
|
|
2 |
|
|
K |
2 |
|
|
|
|
|
|
i=1 σ |
|
|
|
σ |
ε |
|
i |
|||
K
∑Ci Si . (5.6)
i=1
Иначе говоря, величина S является выпуклой функцией отдельных функций распределения, если последние рассматривать как выпуклое подмножество линейного пространства.
Доказательство утверждения. Достаточно доказать, что соот-
ношение (5.6) справедливо для K = 2, так как затем методом полной математической индукции можно показать справедливость выражения (5.6) и для любых конечных значений K. Пусть
q(ε) = C1q1(ε) + C2q2(ε); C1 + C2 = 1; Ci ≥ 0. |
(5.7) |
Тогда |
|
|
0 ≤ (σ |
ε12 |
−2 σ |
ε |
22 |
|
|
1 )2 |
|
|
|
|
|
(5.8) |
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
2 |
|
|
4 |
|
|
2 |
|
4 |
|
|
2 |
|
||||
2ε1ε |
2σ |
ε |
|
|
σ |
|
(5.9) |
|||||||||||||||
σ1 |
≤ σ2 |
|
+1 |
|
2 |
ε |
2 |
1 . |
||||||||||||||
Умножим левую и правую части неравенства (5.9) на произве- |
||||||||||||||||||||||
дение C1C2 и разделим на σ 12σ |
22 , тогда получим |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
σ |
12ε |
|
22 |
|
|
σ ε |
22 |
|
12 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2C1C2 ε1ε 2≤ |
C1C2 |
|
|
|
+ |
|
|
|
|
|
|
|
|
. |
(5.10) |
|||||||
|
σ |
2 |
|
|
σ |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
||||
Прибавим к левой и правой части неравенства (5.10) выражение C12 ε12 + C22 ε 22 и раскроем скобки в правой части, получим
C12 ε12 + C22 ε |
22+ 2C1C2ε |
ε1 |
≤ |
2 |
|
|
Cε12 |
+12 Cε 22+ |
22 |
(5.11) |
||||
+ C C ε 2 σ 1 + C C |
ε 2σ |
2 . |
|
|||||||||||
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||
1 2 2 |
|
|
1 2 1 σ |
|
|
|
|
|
||||||
σ 22 |
|
12 |
|
|
|
|||||||||
Преобразуем правую часть неравенства (5.11) следующим образом:
|
2 |
|
2 |
|
|
|
|
2 σ |
22 |
|
|
ε |
12 |
2 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||||||
C |
|
ε |
|
+ C C |
ε |
|
|
|
|
|
= |
C |
|
|
(Cσ + Cσ |
|
) ; |
(5.12) |
|
|
|
|
|
σ |
12 |
|
|
|
|
||||||||||
1 |
|
1 |
1 2 |
|
|
1 |
|
|
1σ 12 |
1 1 |
2 2 |
|
|
||||||
89
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 σ 12 |
|
|
|
|
|
|
|
|
|
|
ε |
|
|
22 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
C |
|
|
ε |
|
|
|
+ |
C C |
|
ε |
|
|
|
|
|
|
|
|
= |
|
|
C |
|
|
|
|
|
|
|
|
|
|
(Cσ |
|
|
+ Cσ |
|
|
) . |
|
(5.13) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
σ |
|
22 |
|
2σ |
|
22 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
1 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|||||||||||||||||||||||||
Тогда |
правую |
|
|
|
часть |
|
неравенства |
|
|
|
(5.11) |
|
можно |
представить |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
σ 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2σ 12 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
C |
|
|
ε |
|
|
|
+ |
|
C |
|
ε |
|
|
+ C C |
ε |
|
|
|
|
|
|
|
|
|
+ |
|
|
C Cε |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
1 2 1 |
|
|
σ 12 |
|
|
|
|
|
|
|
|
1 2 2 σ |
22 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ε12 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ε |
22 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
= C |
|
|
|
|
|
|
(C |
σ |
|
|
+ |
|
|
Cσ |
|
|
|
|
+) |
|
|
|
C |
2σ |
|
|
|
|
|
|
(Cσ |
+ |
|
|
σC |
|
= |
) |
(5.14) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 σ 12 |
|
1 1 |
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 |
|
|
|
2 2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
ε12 |
|
|
|
|
|
|
|
|
|
|
ε |
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
= (C σ + Cσ |
|
|
|
|
) C |
|
|
σ |
+ |
|
|
|
|
|
C |
|
σ |
|
|
2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Разделим левую |
и |
|
|
|
правую |
|
|
части |
|
|
|
неравенства |
(5.11) |
на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
(C1σ 12+ Cσ2 |
22 ) , тогда с учетом (5.14) и того, что левая часть неравен- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ства (5.11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
C12 ε12 + C22 ε |
22+ 2C1C2ε |
ε1 |
=2 |
|
|
|
(Cε 1+1 |
|
Cε 2 |
|
2 )2 , |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(C1 ε1 + C2ε |
2 )2 |
|
|
≤ |
|
C ε |
|
12 |
|
+ |
|
C ε |
|
|
22 |
. |
|
|
|
|
|
|
(5.15) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
C1σ 1+ Cσ2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
1 |
|
|
|
|
|
|
σ |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Если выражение, стоящее в знаменателе левой части неравен- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ства (5.15), дополнить членом C1C2 (ε1 − ε |
2 )2 , то получим |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
C σ + Cσ + C C(ε − ε =)σ |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Тогда неравенство (5.15), с учетом того, что (C1 ε1 + C2ε |
2 )2= ε |
|
2 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
запишется в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
2 |
|
|
≤ |
|
|
C |
|
|
|
ε12 |
|
+ |
|
|
|
C |
|
|
ε |
22 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.16) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
ε |
|
|
|
|
σ |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, утверждение 1 справедливо для конечного значения K. Это утверждение можно обобщить на тот случай, когда функция распределения q(ε) является выпуклым наложением бесконечно большого числа функций распределения qi(ε):
90
