Работа № 5.Итерационные циклы

Итерационным называется цикл, число повторений в котором заранее определить нельзя. Окончание такого цикла чаще всего происходит при дости­жении заданной точности расчета, а количество повторений зависит от вида вычисляемой функции, от выбора на­чального приближения и от точности вычислений.

Задание.Разработать блок-схемы и составить программы для решения нижеследующих задач.

1. Найти корень уравнения Х – 0,5Аsin(Х/А) + В = 0 методом последовательных приближений (методом итерации) с заданной степенью точности расчётаЕ при начальном приближенииХ₀.

Пояснение.Чтобы воспользоваться методом итерации, необходимо исходное уравнение привести к видуХ_i+1=F(Х_i). В простейшем случае это может быть сделано выражением одного из аргументов, например, так:Х_i+1 = 0,5Аsin(Х_i/А) – В, где обозначенияХ_iиХ_i+1следует понимать как задаваемое (предыдущее) и расчётное (последующее) значенияХ.

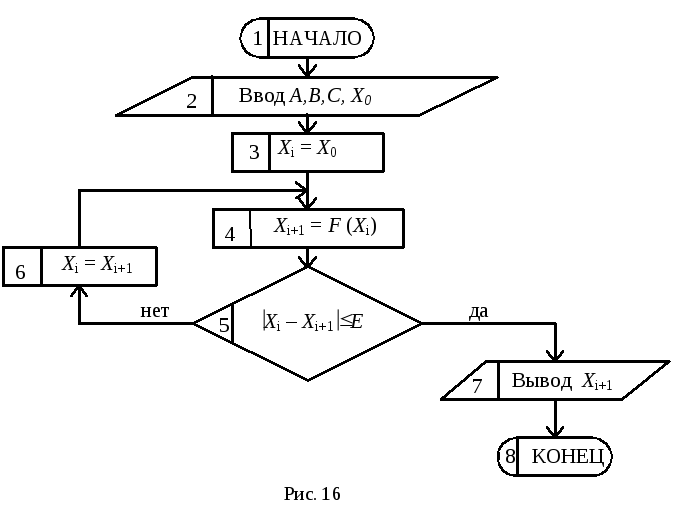
В идеальном случае Х=Х_i=X_i+1, что соответствует точному значению корня.

Блок-схема решения задачи приведена на рис. 16. Здесь в блоке №3Х_iпринимается равным заданному начальному значению Х₀(подготовка цикла), а затем в теле цикла вычисляется значениеХ_i+1. В блоке №5 производится проверка точности расчёта: если разница между предыдущимХ_iи последующимХ_i+1значениями по модулю меньше или равна степени точности расчётаE, то цикл заканчивается; в противном случаеХ_iполучает новое значение в блоке №6 и цикл повторяется заново.

2. Найти сумму бесконечного ряда

Вычисление закончить, если очередное слагаемое по модулю окажется меньше заданной степени точности расчёта Е.

П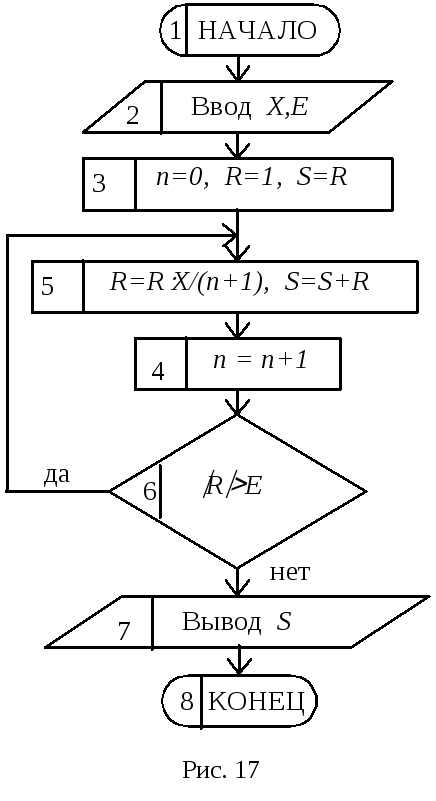ояснение.При вычислении сумм рядов прежде всего необходимо иметь формулу для нахождения очередного члена рядаR. В данном примере каждый новый член рядаR_n+1можно легко подсчитать по значению предыдущегоR_n , а именно:R_n+1=R_nX/(n+1), гдеn– номер текущего члена ряда,n= 0,1,2, и т.д. Приn=0 имеем начальное значение для первого члена рядаR=1, и начальное значение суммы ряда составляет этот единственный первый член рядаS =R.

Блок-схема решения приведена на рис. 17, причём в представляемом варианте различатьR_nиR_n+1нет необходимости, поэтому индексы у них опущены.

3. Организовать итерационный цикл для вычисления корня N-й степени

Расчёт вести по итерационной формуле Ньютона

с заданной степенью точности Е. В качестве начального приближения принять подкоренное выражение. Организовать подсчет количества итераций (количества повторений цикла).

4. Решить уравнение

2АХ– ВХ²= 0,7е^-2Х

относительно Хметодом итерации с точностью доЕ. Начальное приближение принять равным 0. Ввести ограничение на количество итераций: закончить вычисления при числе итераций больше 100. Вывести все последовательные приближения корня и порядковый номер итерации.

5. Для данного вещественного Х вычислить суммуYряда с заданной степенью точности (считать, что требуемая точность достигнута, если очередное слагаемое ряда по модулю меньшеЕ):

а)

б)

в) (для 0Х2)

г)

Контрольное задание № 5. Найти корень уравненияF(X) = 0 на интервале изоляции [A,B], воспользовавшись методом итерации. Работу выполнить в соответствии с представленными ниже пояснениями.

Таблица 5

№	Уравнение F(X) = 0	A	B
1		2	3
2		0	2
3		0,4	1
4		0	0,5
5		1	2
6		-0,5	0
7		0	0,9
8		3	4
9		1	2
10		0	0,9
11		0	1
12		1	2
13		1,2	2
14		3	4
15		1	2
16		0	1,5
17		1	3
18		0	0,9
19		0,5	1
20		1	2
21		0	1
22		2	3
№	Уравнение F(X) = 0	A	B
23		0,4	1
24		-1	-0,2
25		2	3
26		0,2	1
27		1	2
28		1	2
29		0	0,9
30		2	3

Пояснения.

A. Подготовка уравнения, пригодного для итерации

Заданное уравнение F(X)=0 при решении методом итерации должно быть преобразовано к видуХ=φ(X), для которого обязательно выполнениеусловия сходимости,записанного в виде φ'(Х)1, то есть модуль производной от φ(X) на заданном интервале изоляции корня [A,B] должен быть меньше 1. Возможны два способа получения уравнения видаХ= φ(X).

Первый способзаключается в простом выделении какого-либоX из исходного уравненияF(X) = 0, как это было сделано в примере первого задания данной работы. После этого необходимо взять производную от правой части полученного уравнения φ'(X) и подставить в нее поочередноX=AиX=B. Если при этом |φ'(A)|<1 и |φ'(B)|<1, то уравнениеХ=φ(X) считается пригодным для решения методом итерации. Однако такой подход равносилен лотерее: можно выделять различныеX из исходного уравнения, но так и не получить решение, удовлетворяющее условию сходимости.

Второй способдает гарантированное решение, поскольку в основе его изначально заложено выполнение условия сходимости. Заключается он в следующем.

Исходное уравнение F(X) = 0 заменяется на эквивалентное:

Х=Х–F(X) /K,

где К– коэффициент, обеспечивающий сходимость итерационного процесса, выбирается на основании двух требований:

1. знак К должен совпадать со знаком производнойF'(X) на данном интервале изоляции корня [A,B];

2. значение Кпо модулю должно быть больше половины максимального значения модуля производной на интервале изоляции корня [A,B]:

Например, при решении уравнения F(X)=X³–X–1 = 0 на интервале [1,2] находим:

1. F' (X) = 3X²-10 , то естьКдолжен быть положительным;

2. F' (X)_max = 11 , то естьК11/2. ВозьмёмК= 6.

Тогда окончательное уравнение, пригодное для решения методом итерации, будет иметь вид

, гдеK=6.

Б. Реализация вычислительного процесса

При разработке программы необходимо выполнить следующее.

1. В качестве начального приближенияХ₀взять любое число из интервала [A,B], напримерХ₀= (А+В) /2.

2. Степень точностирасчётаЕвыбрать такой, чтобы обеспечить достоверность на менее четырёх старших разрядов в искомом результате.

3. Во избежание «зацикливания» предусмотреть ограничение максимального количества итераций, заканчивая вычисления при числе итераций более 100.

4. Предусмотреть вывод вычисляемого корня и количества затраченных итераций.

5. Произвести следующий вычислительный эксперимент:

   1. Если уравнение для итерации получено первым способом, то построить зависимость количества итераций от значения степени точности вычислений E.

   2. Если уравнение для итерации получено вторым способом, то построить зависимость (график) количества итераций от коэффициента сходимости Kи найти область значенийK, в которой количество итераций будет минимально.

Работа № 6.Сложные циклы

Сложным,иликратным, или вложеннымназывается цикл с несколькими независимыми друг от друга параметрами циклов. Организуются такие циклы путем вложения одного простого цикла внутрь другого, то есть образованием конструкции «цикл в цикле». Количество вложений практически не ограничивается.

Задание.Разработать блок-схемы и составить программы вычисления нижеследующих функций.

1. Сосчитать значения функции Z:

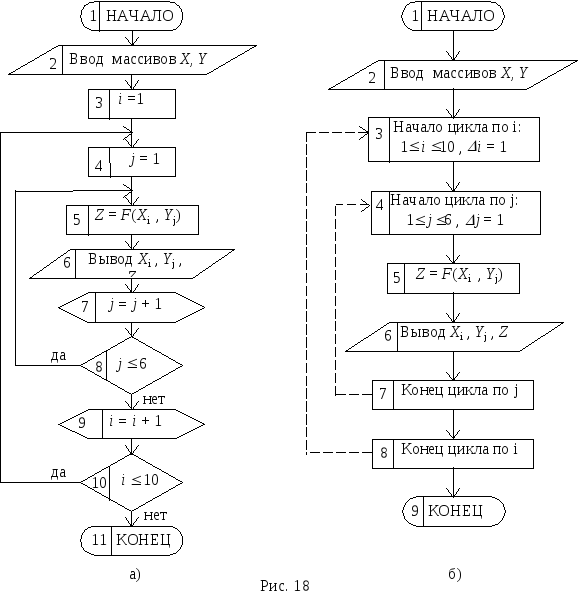
для X=X₁,X₂, … ,X₁₀;Y=Y₁,Y₂, … ,Y₆.

Блок-схема решения задачи представлена на рис.18 в двух вариантах.

2. Рассчитать таблицу корней кубических 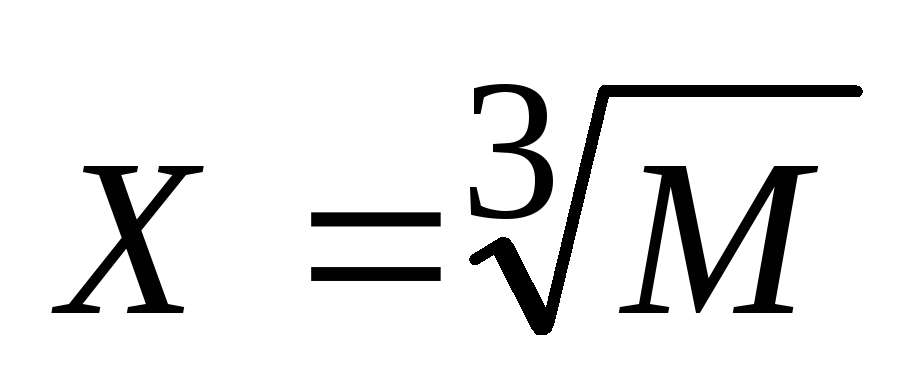для значенийМ от 10 до 1000 с шагом 5. Расчёт вести методом последовательных приближений по формуле

с заданной степенью точности Е. В качестве начальных приближений приниматьX₀=М/5 .

Пояснение. Блок-схема решения приведена на рис. 19 и представляет собой арифметический цикл с простой переменной, организующий задание и изменениеM, внутрь которого вложен итерационный цикл вычисления кубического корня изM.

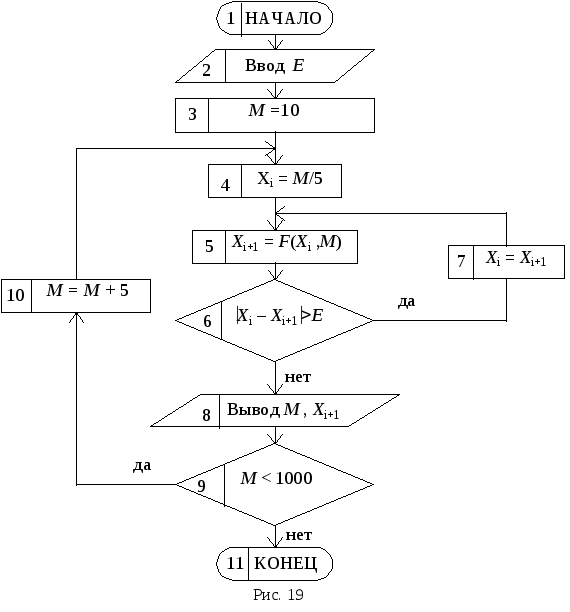
3.

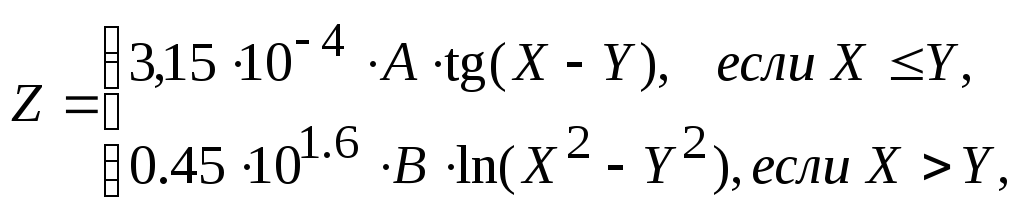
для X=X₁, X₂,…,X₁₀ ; 3 ≤ Y ≤ 5; ∆Y = 0,25.

Все результаты сохранить в массиве Z₁. Сосчитать сумму и количество результатов Z  .

4.

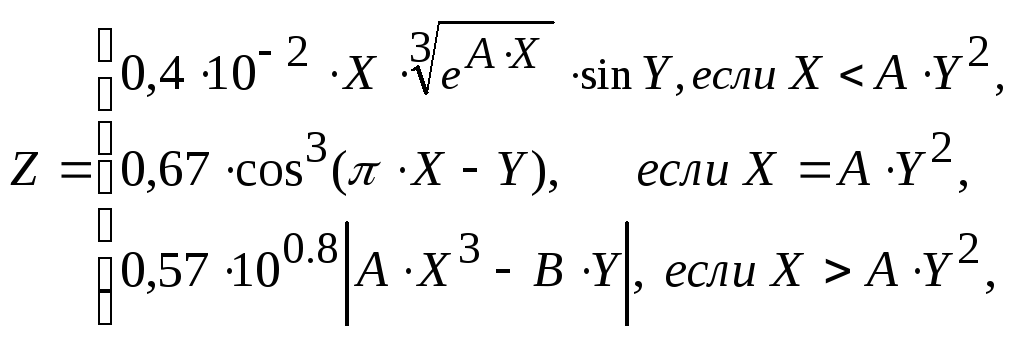
для X=X₁ , X₂ ,…,X₁₀ ; Y=Y₁, Y₂, …,Y5.

Результаты сохранить в двумерном массиве Z₂, содержащем три столбца: X, Y, Z. Найти минимальный и максимальный результаты, выбрать из них максимальный по модулю.

5. Найти действительные корни уравнения

методом итерации с заданной степень точности E на отрезке [0, π/A ] для A = A₁, A₂, …, A₄₅.

Результаты сохранить в массиве Y. Отыскать минимальное значение корня и его аргумент A .

6. Расcчитать значение суммы ряда

для всех Х в интервале от –0,8 до 0,8 с шагом 0,1. Вычисление суммы производить с заданной степенью точности Е=10^-4 .

7. Для матрицы А (1020) рассчитать средние арифметические значения отрицательных элементов каждой строки и средние геометрические значения положительных элементов каждой строки. Из результатов вычислений сформировать массив A1 средних арифметических и массив А2 средних геометрических.

Контрольное задание № 6. Вычислить сумму членов ряда

для одиннадцати равноотстоящих значений X на интервале [X_H , X_K]. Общая формула для К-го члена ряда приведена в таб­л. 6, а величина К принимает следующие значения:

а) К = 0 ,1, 2, 3, ... , N

для вариантов 1,3,5,6,7,9,10,11,13,17,19,20,21,22,25;

б) К = 1, 2, 3, ... , N

для вариантов 2,4,8,12,14,15,16,18,23,24,26,27,28,29,30.

Для контроля правильности нахождения суммы при каждом X предусмотреть одновремен­ное вычисление и вывод значения функции Y=F(X), представляющей точное зна­чение соответствующей суммы ряда при N  .

Пояснение. Алгоритм решения задачи представляет собой сложный цикл, в котором внутренний цикл должен вычислять ряд (суммировать члены ряда) при заданном фиксированном аргументе X, а внешний организует задание и из­менение X в интервале от Х_Н до Х_К.

В ряде случаев вычисление очередного члена ряда по об­щей формуле затруднено. Наиболее часто такими причинами являются:

– наличие факториала K!, для расчета которого пришлось бы организовать специальный цикл, осуществляющий вычисление произведения сомножителей целого типа от 1 до K;

– наличие сомножителя в виде аргумента X в целой степени. В этом случае обычное возведение в степень через логарифмирование, во-первых, может быть не целесообразно по времени вычислений, а во-вторых, может быть совершенно непригодно для отрицательных аргументов, что приведет к организации цикла вычисления произведения многих сомножителей.

Поэтому в подобных случаях це­лесообразно использовать рекуррентные соотношения, то есть вычислять каждый последующий член ряда через предыдущий. Это позволяет существенно упростить программу и сократить объем вычислительных операций.

Например, пусть общая формула для К-го члена ряда имеет вид

.

В формуле присутствуют оба отмеченных выше «неудобных случая»  и факториал, и целая степень аргумента. Поэтому следует получить рекуррентную формулу для (K+1)-гo члена ряда. Для этого выполним замену K на K+1 и в образованной формуле выделим в качестве сомножителя предыдущий член ряда:

.

Последняя формула чрезвычайно проста для вычислений, а ее реализация приведена в первом примере работы №5.

В некоторых случаях рекуррентные соотношения полезно записывать не для полной формулы члена ряда, а только для ее части, вы­деленной в отдельный сомножитель, а оставшуюся часть вычислять не­посредственно. Например, если

, то полагаем и вычисляем рекуррентно, а сомножительнепосредственно.

В случае знакопеременных рядов, содержащих (-1) в степени, зависящей от номера члена ряда, в простейшем случае можно выделить отдельный сомножитель только для вычисления такой степени. Например, если в формуле для члена ряда выделить сомножитель

,

то рекуррентная формула для него будет иметь вид

.

То есть в этом случае учет смены знака в программе сводится к тривиальной операции С = С для знакопеременного сомножителя.