algem

6) Базис на прямой на плоскости, в пространстве. Разложение вектора по базису. Базисом на прямой называется любой ненулевой вектор на этой прямой.Этот вектор называется базисным, тогда любой вектор a, коллинеарный этой прямой может быть разложен по базису. Пусть a,b,…,z векторы, α,β,….ω числа. Вектор αa+βb+…+ωz называется линейной комбинацией векторов a,b,…z, а числа α,β,….ω-коэффициентами линейной комбинацию. Базисом на плоскости называются 2 неколлинеарных вектора e1,e2 на этой плоскости, взятые в определенном порядке. Эти векторы называются базисными. a=x1*e1+x2*e2 Любой вектор a ∈ плоскости м.б. разложен по базису e1 и e2 на этой плоскости. Базис на плоскости называется правым, если кратчайший поворот от первого вектора ко второму происходит против часовой стрелки. Левым базисом, если по часовой стрелке. Базисом в пространстве называется 3 некомпланарных вектора e1,e2,e3, взятые в определенном порядке. a=x1*e1+x2*e2+x3*e3. Любой вектор a м.б. разложен по базису e1,e2,e3 в пространстве т.е. представлен в виде линейной комбинации. Пусть I,j,k единичные векторы (орты) направленные вдоль координатных осей X,Y,Z соответственно. Если смотреть с конца вектора k, то движение вектора i по короткому пути происходит против часовой стрелки. В этом случае говорят, что I,j,k правая тройка векторов, иначе левой.

9)Смешанное произведение. Определение, св-ва, геометрический смысл, выражение в координатах. Определение: смешанным произведением векторов a,b,c называется число [a;b]c, которое обозначается abc=[a,b]c. Геом.смысл: пусть V- объем параллелепипеда, построенного на векторах a,b,c; a,b,c=V если тройка правая. A,b,c=-V если тройка левая. |abc|=V. Св-во смешанного произведения: abc=0 тогда abc-компланарны, т.е. параллельны одной плоскости. (считаем, что если среди a,b,c есть два коллинеарных вектора или(и) один из них нулевой, то a,b,c автоматически компланарны). A={x1;y1;z1} B={x2;y2;z2} C={x3;y3;z3} abc=(выражение в координатах)

10)Плоскость в пространстве. Нормальный вектор плоскости. Различные виды записи уравнения плоскости. Рассмотрим плоскость P, проходящую через M0(x0;y0;z0) ┴ вектору N={A,B,C}, который называется нормалью к плоскости P. Пусть N≠0 т.е. Пусть M(x,y,z)-произвольная точка на плоскости. Вектор ={x-x0;y-y0;z-z0} лежит в плоскости тогда 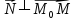; N*=0; Тогда (скалярное призведение) A(x-x0)+B(y-y0)+C(z-z0)=0; Уравнение плоскости через точку (x0;y0;z0) с нормалью N={A,B,C} Раскрыть скобки и обозначить свободные член D. Ax+By+Cz+D=0; P1: A1x+B1y+C1z+D1=0; P2: A2x+B2y+C2z+D2=0 P1┴P2N1┴N2N1*N2=0; A1A2+B1B2+C1C2=0(Условие перпендикулярности 2-х плоскостей) M1(x1;y1;z1); M2(x2;y2;z2); M3(x3;y3;z3); P-плоскость через M1,M2,M3. Возьмем произвольную точку M(x,y,z) M∈P то векторы M1M; M1M2; M1M3- компланарны =0 Уравнение плоскости проходящей через 3 заданные точки.

11)Расстояние от точки до плоскости. Отклонение точки от плоскости. Пусть даны плоскость P: Ax+By+Cz+D=0 и точка M*(x*,y*,z*) Расстояние от M* до плоскости есть длина перпендикуляра, опущенного из M* на P. Она вычисляется по формуле: d= длина нормали N. Если точка M*∈P то числитель равен 0;d=0. Отклонение точки от плоскости:δ=x0cos(α)+y0cos(β)+z0cos(γ)-p или d= где знак перед корнем противоположен знаку D, если D≠0, и выбран произвольно, если D = 0.

12) Прямая в пространстве. Направляющий вектор прямой. Различные виды записи уравнения прямой в пространстве. Рассмотрим прямую L в пространстве проходящую через точку M0(x0;y0;z0) || вектору a={l,m,n} который называют направляющим. Пусть M(x,y,z)-произвольная точка на прямой ||a Условие коллинеарности векторов и a состоит в пропорциональности их координат. =(канонические уравнения прямой в пространстве) ==t тогда x=x0+lt; y=y0+mt; z=z0+nt; При любом t соотношения определяют точку (x,y,z) на прямой, проходящей через точку M0(x0;y0;z0) с направлением вектором a{l,m,n}. Они называются параметрическими уравнениями прямой. A1x+B1y+C1z+D1=0; и A2x+B2y+C2z+D2=0 (плоскости) N1={A1;B1;C1}, N2={A2;B2;C2}(отличны от нуля и НЕ коллинеарны, т.е. нет пропорциональности, тогда плоскости пересекаются по прямой. В системе полагаем z=z0=0. Тогда получаем систему относительно двух переменных, решение которой можно найти по методу Крамера. Получаем точку M0(x0;y0;z0)(z0=0) a┴N1; a┴N2; a=[N1;N2] Вычисляем смешанное произведение и переходим к записи канонических и параметрических уравнений.

13) Прямая на плоскости. Различные виды записи уравнения прямой на плоскости. Общее уравнение прямой на плоскости имеем вид: Ax+By+C=0, где М >0 Расстояние от точки M(x*; y*) до прямой вычисляется по формуле: d= Уравнение прямой с угловым коэффициентом y=kx+b; tgα=k; α-называется углом наклона k=tgα угловым коэффициентом. При положительном k имеем возрастающую линейную ф-цию(причем, чем больше k, тем быстрее рост), при k<0 убывающую. Y=y0=k(x-x0); M1(x1;x2) M2(x2;y2); y-y1=; y=k1x+b1; y=k2x+b2; при k1=k2 прямые параллельны. При k1*k2=-1 прямые перпендикулярны. tgω=

14)Кривые второго порядка на плоскости. Эллипс. Гипербола. Парабола. Канонический вид и св-ва. Эллипс. Эллипсом называется гмт, сумма которых расстояний от которых до двух заданных точек(фокусов) есть величина постоянная и большая, чем расстояние между фокусами. ; a>0; b>0 определяет эллипс и называется каноническим уравнением эллипса. a и b-полуоси эллипса. a>b a-большая, b-малая полуось Координатные оси служат осями симметрии. Центр симметрии (0;0) При a=b эллипс превращается в окружность. Фокусы имеют координаты (-c;0) (c;0) c>0 определяется из условия Эксцентриситет это величина ε= Для эллипса 0≤ε<1. Точки (-a;0) (a;0) (0;-b) (0;b) принадлежат эллипсу и называются его вершинами. Гипербола.-это гмт, для которых модоль разности от двух фиксированных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. каноническое уравнение гиперболы. a>0 b>0-полуоси гиперболы a- действительная; b- мнимая. Фокусы имеют координаты (-c;0) (c;0) где c находится из условия Прямые y=b/ax y=-b/ax называются асимптотами гиперболы. Эксцентриситет ε=c/a>1 Оси координат служат осями симметрии, а начало координат O(0;0) –центром симметрии. Точки (a;0) и (-a;0) называются ее вершинами. Парабола-гмт, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой называемой директрисой. Уравнение p>0 определяем параболу и называется ее каноническим уравнением. Фокус параболы есть точка F(p/2;0), а уравнение директрисы имеет вид: x=-p/2 Парабола симметрична относительно оси Ox. Вершина параболы находится в начале координат.

15)Общее уравнение 2-ого порядка, типы линий. Приведение общего уравнения к каноническому виду (при помощи сдвига и поворота осей координат) где Q(x,y)-квадратичная форма. матрица квадратичной формы. ∆=AC-B*B; l(x,y)=Dx+Ey-линейная форма. 2Dx+2Ey+F-линейная ф-ция. Уравнение определяет эллипс, гиперболу, параболу и еще: пару прямых А) пересекающихся , y=x;y=-x Б) параллельных В)совпадающих ; Линии второго порядка классифицируются по следующим 3 типам: Эллиптический(AC-B*B>0), гиперболический AC-B*B<0, параболический AC-B*B=0; Если AC-B*B≠0 то линия имеет центр C(x0;y0) который можно найти из системы Ax0+By0+D=0; Bx0+Cy0+E=0; Далее перенос начала координат с помощью параллельного сдвига осей в точку С и x’ и y’-новые координаты. x=x0+x’; y=y0+y’ тогда 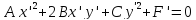; F’=Dx0+Ey0+F. матрица преобразования. Система система определяет угол поворота. Эти выражения следует подставить в каноническое уравнение, раскрыть скобки и собрать подобные члены, затем коэффициент при произведении положить равным нулю, определить угол поворота. После этого мы приходим к каноническому виду и выясняем тип линии.

16)Общее уравнение поверхности 2-ого порядка. Основные уравнения в канонической форме.

+2Dxy+2Exz+2Fyz+2Gx+2Hy+2Kz+L=0; +2Dxy+2Exz+2Fyz-квадратичная форма матрица квадратичной формы. Эллипсоид. a>0;b>0;c>0 полуоси эллипсоида. Если положим z=0 то получим в сечении эллипс. Если a=b=c=R то эллипсоид превращается в шар радиуса R. 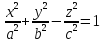–однополостный гиперболоид двуполостный гиперболоид (p>0;q>0) гиперболический параболоид(седло) коническая поверхность.

17)Арифметическое линейное подпространство. Примеры. Упорядоченные наборы из n чисел будем называть векторами или n-мерными векторами. X=(x1,…,xn) y=(y1,…,yn) x+y=(x1+y1,…,xn+yn) Пусть λ – число, то λx=(λx1,…, λxn) Сложение и умножение происходит покоординатно. Пространством Rn называется множество всех n-мерных векторов c покоординатным сложением и умножением на скаляр. Скалярное произведение: (x;y)=x1y1+…+xn*yn. Модуль вектора: |x|= p(x,y)=|y-x|= cosφ= Надо быть уверенным, что выражение справа не превосходит единицы или |(x,y)|≤|x|*|y| Неравенство Коши-Буняковского: имеет место неравенство, причем знак равно возможет только тогда, когда x||y. Док-во. Рассмотрим ф-цию φ(t)=(x-ty,x-ty)=(x,x)-2t(x,y)+t*t(y,y) ф-ция неотрицательна при любом t, потому что представляет квадрат длины. Квадратный трехчлен относительно t неотрицателен при всех t в случае, когда его D≤0. D=4(x,y)*(x,y)-4(x,x)(y,y)≤0

18)Линейная зависимость и независимость векторов в Rn, базис. Разложение вектора по базису. Система векторов a1,a2,…an называется линейно независимой, если из равенства нулевому вектору линейной комбинации этих векторов. λ1a1+…+λmam=0 вытекает, что все коэффициенты λ1=λ2=…=λm=0 линейная комбинация с нулевыми коэффициентами называется тривиальной. Линейная независимость означает, что ни один их векторов системы не является линейной комбинацией остальных. Система из одного вектора {a} л.н если и только если a≠0. Система {a1;a2}(л.н.) то a1 не коллинеарен a2. Система векторов называется ортогональной если она все ненулевые и (ai,aj)=0 ∀i≠j т.е. различные векторы попарно ортогональны. Утверждение. Ортогональная система л.н.. Пусть a1,a2,…an базис в Rn тогда всякий вектор x∈Rn можно разложить по базису,т.е. представить в виде линейной комбинации. Лемма разложение по базису единственно. Док-во: пусть есть другое разложение: x= Вычтем отсюда x=; 0=(-; В силу линейно независимости векторов базиса имеем: (=0,…,-=0. Рассмотрим систему e1=(1,0,…,0) e2=(0,1,0…,0) e3=(0,…,1) Она ортогональна и следоват. Л.н. Поскольку элементов n, то это базис. Он называется стандартным или каноническим базисом Rn. Разложение вектора x=(x1,x2…xn) выглядит x=x1e1+x2e2+…+xn*en. |e1|=|e2|=…=|en|=1 Благодаря этому базис e1,…,en называют нормированным. Поскольку он еще ортогональный, то его называют ортонормированным.

19)Подпространство. Линейная оболочка системы векторов. Базис в подпространстве. Определение: множество E∈Rn называется подпространством если: 1) сумма 2-ч любых векторов из E снова ∈ E. Произведение любого вектора из E на скаляр есть вектор из E. Подпространство замкнуто относительно операций сложения и умножения на скаляр. Пример подпространства: a-ненулевой вектор в Rn рассмотрим множество: {x∈Rn|(a,x)=0}-гиперплоскость, состоящую из векторов, ортогональных вектору а. Множество {x∈Rn|(a,x)=1} Множество состоящее из нулевого вектора {0} есть подпространство в Rn и все Rn есть подпространство самого себя. Пересечение двух и более подпространств есть подпространство. (a1,x)=0…(am,x)=0. Определяет подпространство в Rn. Базис подпространства определяется точно также как и базис в Rn. Пусть E∈Rn-подпространство. Система л.н.векторов a1,…am. Число элементов базиса подпространства постоянно и называется размерностью подпространства dim V=k V=Rn; dimRn=n

20)Ранг системы векторов. Ранг матрицы. Приведение матрицы к ступенчатому виду. Пусть даны векторы a1,a2,…am в пространстве Rn. Рангом системы вектором называется максимальное число л.н. векторов этой системы. Пусть дана матрица A= Горизонтальным рангом матрицы A называется ранг системы ее строк (a11…a1n) (am1…amn) Вертикальным рангом матрицы называется ранг системы ее столбцов …. Ранг матрицы по строкам = рангу матрицы по столбцам. Rстр(A)=Rстолб(A) Определение: рангом матрицы называется max число л.н. строк или столбцов. Эл-т называется угловым, если он отличен он 0, а всюду левее и ниже него все элементы-нули. Высота ступеньки всегда 1,а ширина-произвольная. Ранг матрицы равен числу угловых эл-тов. Следующие преобразования называются элементарными: 1)перестановка строк 2)прибавление к элементам одной строки эл-тов другой строки, умноженной на число. Теорема: с помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду. Пример = rankA=2

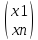21)Системы линейных алгебр. Уравнений. Совместность системы. Т.Кронекера-Капелли. Рассмотрим систему m уравнений с n неизвестными A= x= b= Ax=b Система, имеющая хотя бы одно решение x называется совместной, в противном случае - несовместной. Пусть: ; … тогда систему можно записать в виде x1A1+x2A2+…+xnAn=b Добавим к A столбец b и назовем расширенной матрицей. Т.Кронекера-Капелли: система совместна тогда и только тогда когда rankA=Rank(A|b)(т.е. ранги матрицы системы и расширенной матрицы совпадают)

22)Св-ва решений однородной и неоднородной систем уравнений. Система называется однородной если b=0; если b≠0-система неоднородна. 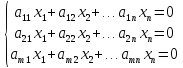Ax=b Утверждение:однородная система всегда совместна, т.к. нулевой вектор-решение. Теорема:множество решений однородной системы представляет собой подпространство в Rn. Док-во: множество решений V∈Rn; Пусть x,y∈V, Ax=0,Ay=0; A(x+y)=Ax+Ay=0+0=0 тогда x+y∈V; x∈V; α∈R; Ax=0, A(αx)=α(Ax)=α*0=0 тогда αx∈V Вывод:V-является подпространством по определению. Теорема: Решение однородной системы + решение неоднородной системы(частное решение) есть решение неоднородной системы. Пусть x’+x” таковы что Ax’=0; Ax”=b A(x’+x”)=Ax’+Ax”=0+b=b. Теорема : разность 2-х решений неоднородной системы есть решение однородной. Ax’=b, Ax”=b тогда A(x’-x”)=b-b=0. Общее решение неоднородной системы есть частное решение неоднородной системы + общее решение однородной.

23) Метод Гаусса для получения общего решения однородной и неоднородной систем уравнений. Приводим A к ступенчатому виду. Главными неизвестными называются неизвестные в столбцах которой есть угловые элементы, если привести матрицу к ступенчатому виду. Остальные переменные, т.е. те, в столбцах которой нет угловых элементов называются свободными или независимыми. Двигаясь снизу вверх выражаем главные переменные через свободные. общее решение в координатной форме. Для построения ФСР нужно взять одну свободную переменную, равную единице, а остальные переменные равные нулю.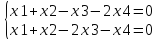 A=  x1,x3-главные, x2,x4- свободные dimV=2; Общее решение в координатной форме. Приведение матрицы к ступенчатому виду это прямой ход метода Гаусса, а нахождение из системы ступенчатого вида называется обратным ходом м. Гаусса. x1={-1;1;0;0} x2={3;0;1;1} ФСР. X=C1x1+C2x2 разложение общего решения по ФСР. Решение неоднородной системы по методу Гаусса. Дана расширенная матрица. Расширенную матрицу к ступенчатому виду. R(A|b)>R(A)-система несовместна. R(A|b)=R(A)-система совместна. Далее выписываем систему, отвечающую ступенчатой матрице и выражаем главные неизвестные через свободные. (A|b)=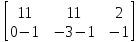 x1,x2-главные; x3,x4-свободные. Общее решение в координатной форме. Общ.реш. неоднородных уравнений. -=; f1={2;-3;1;0} f2={0;-1;0;1} ФСР. =C1x1+C2x2+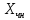

24)Действия над матрицами. Сложение, умножение на число. Произведение матрицы на вектор. Произведение матриц. A= B= C=A+B; ∀I,j; λA-матрица с коэффициентом λ(умножение матриц на число) A(m;n) B(n;k); C=AB C(m;k) AB≠BA(умножение матриц не коммутативно) A= x=∈Rn Ax=y; y=∈Rm i=1,…,m. b= Ax=b

25)Обратная матрица. 2 способа нахождения обратной матрицы. Использование обратной матрицы для решения систем. Пусть A и B квадратные матрицы порядка n. Определение: Матрица B называется обратной к матрице A, если AB=BA=E. Для обратной матрицы B используют обозначение обратная в A. Теорема: Матрица A имеют обратную тогда и только тогда, когда detA≠0. Матрица, у которой определитель ≠ 0, т.е. существует обратная, называется невырожденной. 2способа нахождения обратной матрицы. 1)Метод присоединенной матрицы. A= -невырожденная матрица.A(n,m) тогда 1) вычисляем алгеб. Дополнения. 2)Транспонируем матрицу из дополнений. 3) Разделим полученную матрицу на определитель A. 2) С помощью элементарных преобразований добьемся того, чтобы на месте матрицы A оказалась бы единичная матрица E. (A|E)(E|) A= detA≠0 x=∈Rn Ax=b; b=∈Rn (Ax)= b; (Ax)=(A)x=Ex=x; x=b

26)Применения линейной алгебры в экономике. Модель «затраты - выпуск». Основные задачи. Имеется предприятие, выпускающее n видом продукции в количествах x1,x2,x3,…xn. Вектор x=∈Rn план выпуска. При этом расходуется m видов ресурсов, имеющихся в количествах b1,b2,…bm. Соответственно. b=-вектор ресурсов. Известны расходные коэффициенты -кол-во i-го ресурса необходимого для пр-ва единицы j-uj продукта. i=1,…,m,j=1. A=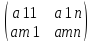-матрица расходных коэффициентов.(технологическая матрица). При плане x расход i-го ресурса составит величину ai1x1+…+ainxn=yi; i=1,…,m. Ax=y-вектор расходов ресурсов. 1)расходы не превышают запасы y≤b, Ax≤b 2)расходуются все ресурсы: y=b; Ax=b 3)запасы ресурсов b и матрица расходных коэффициентов A. Требуется определить план выпуска x(решить Ax=b) Если m=n; detA≠0; x=. Нас интересуют планы x≥0, т.е. xi≥0,…,xn≥0. Пример задачи: дан план x, найти расход ресурсов y. Решение:Ax=y.

27)Применение линейно алгебры в экономике. Модель межотраслевого баланса. Основная задача межотраслевого баланса. Продуктивная матрица. Модель межотраслевого баланса. Xi-общий (валовый) объем продукции i-той отрасли. Xij-объем продукции i-той отрасли, потребляемой j-той отраслью (I,j=1,…,n) yi-объем конечного продукта i-той отрасли. = i=1,…,n общ. продукт = продукт, потребляемый n-отраслями+конечный продукт. -технологический коэффициент. – затраты продукции i-той отрасли на производство единицы продукции j-той отрасли. x= y= = ; i,j=1,…,n. Линейная зависимость материальных завтра валового продукта. X=AX+Y-линейные и балансовые соотношения. Осн. задача межотраслевого баланса: заданы A,y x-вектор валового продукта. (E-A)X=Y. Если det(E-A)≠0 существует ; X=Y=SY; S=-матрица полных затрат. S= пусть Y=Y’={1;0;0;0} т.е. требуется получить единицу первого конечного продукта, а остальные нули. X== на пр-во единицы продукции каждая отрасль требует s11,s21,…,sn1. X=S=-на выпуск единицы j-го конечного продукта потребуется. S1j,s2j,…,snj. Sij- кол-во полных затрат i-ой отрасли необходимых для пр-ва единицы продукта j-ой отрасли. Продуктивная матрица. y≥0,x≥0;y≥0↔y1≥0,…,yn≥0, x≥0↔x1≥0,…,xn≥0, кроме того aij≥0. Определение. Матрица A называется продуктивной, если для любого вектора y≥0 существует вектор x≥0. (E-A)X=Y. Пусть S=-существует и имеет неотрицательные коэффициенты. Y≥0 то X=SY≥0. Теорема1: если Sij≥0 тогда матрица продуктивная. Теорема2:Пусть A- матрица с неотрицательными элементами(aij≥0) и для любого j-го столбца. j=1,…,n. ∃k такое что 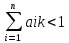тогда A продуктивна.

28)Собственные числа и собственные векторы квадратичной матрицы. Пусть A=-квадратная матрица порядка n. Определение. x∈Rn-называется собственным вектором матрицы A. если 1)λx=Ax λ-называется собственным вектором матрицы A. 2)x≠0. Пример: A=E=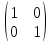-единичная матрица тогда Ex=x ∀x; x≠0-собственный вектор. Характеристический многочлен: λ-собственный число матрицы A тогда ∃x=0, что Ax=λx. (A-λE)x=0 тогда det(A-λE)=0; A-λE=-λ==0(характеристическое уравнение) Теорема: собственные векторы, отвечающие различным собственным значениям, линейно независимы. Пусть λx=Ax, x≠0; Ay=ωy,y≠0. λ≠ω. Пусть x=βy,β≠0 тогда, умножая на A. Ax=βAy, λx=βωy, λ(βy)=βωy. Но β≠0, y≠0. Следовательно λ=ω. Алгоритм поиска собственных чисел и собственных векторов. 1)составляем характеристическое уравнение. 2)Находим вещественные корни характеристического многочлена(если таких нет, то собст. векторов нет) 3)Для каждого корня составляем систему линейных однородных уравнений и находим ФСР.4)Объединяем найденные системы по всем собственным числам. Получаем л.н. систему из собственных векторов матрицы A.

29) Ортогональные системы векторов. Процесс ортогонализации базиса. X и Y в Rn ортогональные если (x,y)=0. Система векторов v1,…,vm в Rn ортогональна, если a)(vi;vj)=0 ∀i≠j b)(vi,vi)>0 ∀i. Ортогональная система линейно независима. Система v1,…,vm называется ортонормированной, если она ортогональна и |vi|=1 ∀i. Если u1,…,um-ортогональная система, то Vi=u1/|u1| ∀i получаем ортонормированную систему. Определение. Пусть a1,…,am- система векторов в Rn. Ее линейно оболочкой, обозначаемой <a1,…,am> или Lin(a1,…,am) называется множество всех линейных комбинаций векторов этой системы, т.е. множество векторов вида. a=λ1a1+…+λmam. Лемма. Пусть {f1;…;fm}-линейно независимая система в Rn. Тогда ее можно ортогонализовать,т.е. существует ортогональная система {g1,…,gm} такая, что Lin(f1,…,fm)=Lin(g1,…,gm) 1)Пусть m=1 т.е. имеет систему {f1} из одного ненулевого вектора. В этом случае g1=f1. 2)Пусть m=2, т.е. имеем систему {f1;f2} Пусть g1=f1; g2=f2-λg1; λ-определяем так, чтобы векторы g1 и g2 оказались ортогональны. (g1;g2)=0; (g1,f2-λg1)=0 (g1,f2)-λ(g1,g1)=0 выражаем λ и получаем g1=f1; g2=f2-g1 следовательно.g1┴g2 и Lin{g1;g2}=Lin{f1;f2} Для произвольного m≤n g1=f1; g2=fk-gi, k=2,…,m

30) Ортогональные матрицы и их св-ва. Пусть U=-квадратная матрица порядка n. Определение. Квадратичная матрица U порядка n называется ортогональной, если ее столбцы образуют ортонормированный базис в Rn, т.е. если для системы столбцов U1,…,Um. Матрицы выполнены условия. a) (Ui,Uj)=0 при i≠j. б) (Ui,Ui)=1 ∀i=1,…n Теорема: Пусть U- квадратичная матрица порядка n. 1)столбцы матрицы U образуют ортонормированный базис в Rn. 2) Строки матрицы U образуют ортонормированный базис в Rn 3)4) (Ux,Uy)=(x,y) ∀x,y∈Rn Св-во 3 означает, что вычисление обратной матрицы сводится к ее транспонированию.(!)