
Лекция 11
.docЛЕКЦИЯ 11. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Задача 1. Решить систему
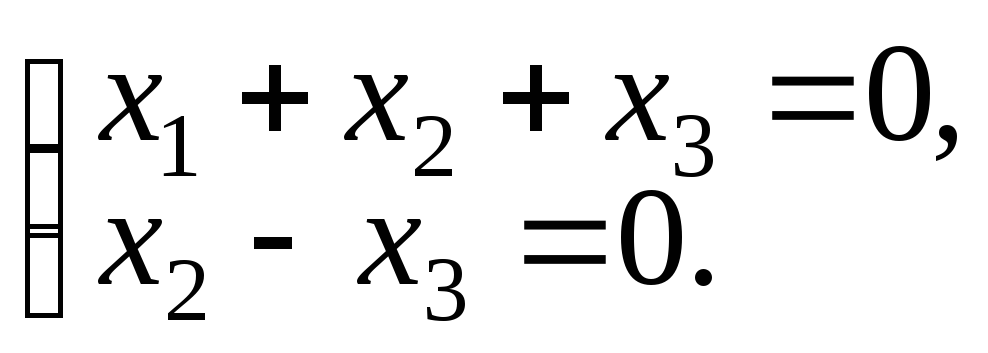 .
.
Решение. Системе двух уравнений с тремя неизвестными соответствует матрица системы
 .
.
Матрица А
имеет ступенчатый вид, угловые элементы
выделены жирным шрифтом
прямой ход метода Гаусса выполнять не
надо. Каждый столбец матрицы состоит
из коэффициентов при переменных, которые
написаны сверху над столбцами. Переменные
![]() ,
в столбцах которых есть угловые элементы,
являются главными или зависимыми;
,
в столбцах которых есть угловые элементы,
являются главными или зависимыми;
![]() - свободная или независимая переменная.
Положим
- свободная или независимая переменная.
Положим
![]() и выразим главные переменные
и выразим главные переменные
![]() через параметр
через параметр
![]() :
:
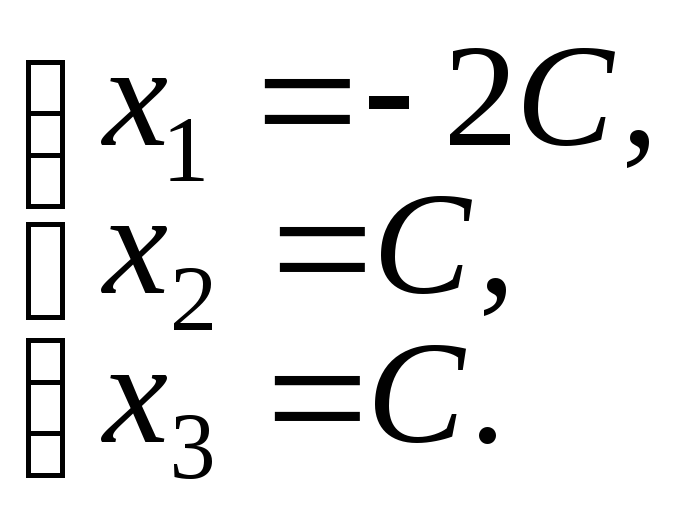
Мы нашли общее решение в координатной форме.
Размерность
подпространстве решений однородной
системы равна количеству независимых
переменных, т.е. одному. Базис (ФСР) в
подпространстве решений однородной
системы состоит из одного вектора,
который можно получить, выбрав
![]() и записывая решение в виде вектора:
и записывая решение в виде вектора:
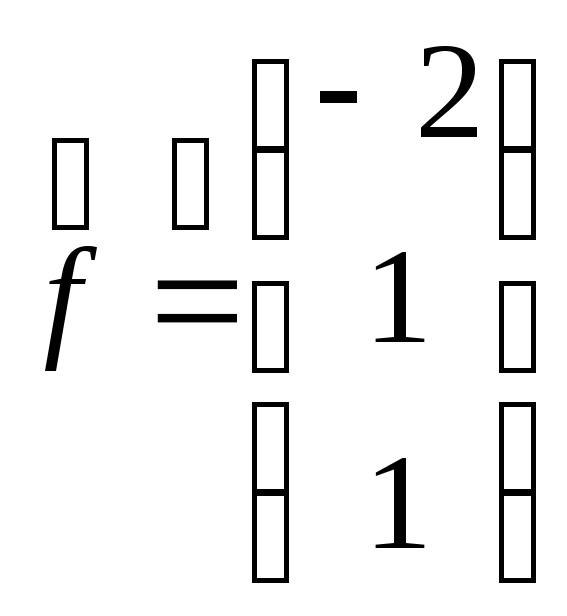
Общее решение однородной системы в векторной форме – разложение общего решения по ФСР имеет вид
![]() .
.
Задача 2.
Найти общее решение и фундаментальную
систему решений однородной системы
![]() .
Разложить общее решение по Ф.С.Р.
Матрица
.
Разложить общее решение по Ф.С.Р.
Матрица
![]() задана.
задана.

Решение. Выпишем систему уравнений в координатной форме
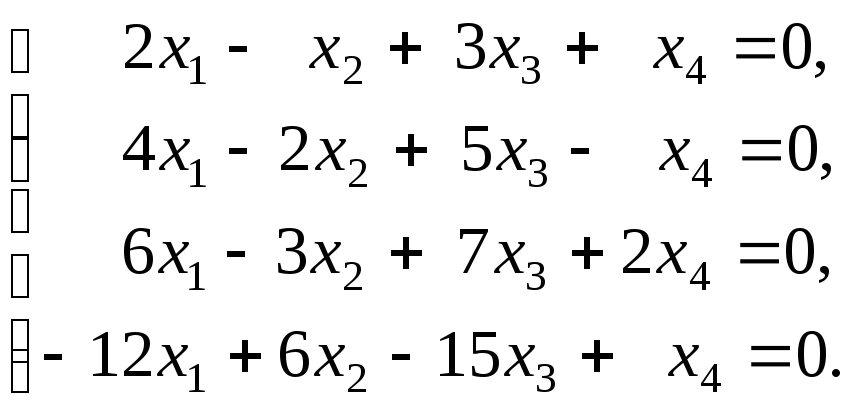
Поскольку вектор
правых частей равен нулевому вектору,
т. е. ![]() ,
то система уравнений является однородной.
,
то система уравнений является однородной.
Методом Гаусса
приведем систему уравнений к ступенчатому
виду. Выпишем матрицу
![]() и преобразуем ее:
и преобразуем ее:
 .
.
На первом шаге
первую строку не меняем (в верхнем левом
углу стоит ведущий элемент
![]() );
из второй строки вычитаем первую,
умноженную на 2,
и результат запишем во вторую строку;
из третьей строки вычитаем первую,
умноженную на 3, и результат запишем в
третью строку; к четвертой строке
прибавляем первую, умноженную на 6,
результат запишем в четвертую строку.
Условно эти элементарные операции можно
записать так:
);
из второй строки вычитаем первую,
умноженную на 2,
и результат запишем во вторую строку;
из третьей строки вычитаем первую,
умноженную на 3, и результат запишем в
третью строку; к четвертой строке
прибавляем первую, умноженную на 6,
результат запишем в четвертую строку.
Условно эти элементарные операции можно
записать так:
![]() .
.
Далее применим
элементарные операции:
![]()
![]() .
Получаем:
.
Получаем:
 .
.
После чего к
четвертой строке, умноженную на 5,
прибавим третью строку, умноженную на
2, результат запишем в четвертую строку,
т. е.
![]() :
:
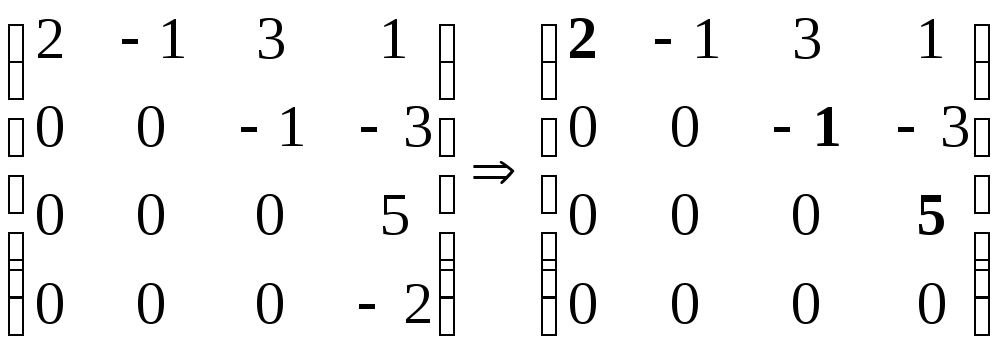
Матрица
![]() приведена к ступенчатому виду. Мы
выполнили прямой
ход метода Гаусса.
приведена к ступенчатому виду. Мы
выполнили прямой
ход метода Гаусса.
Число угловых
элементов (отмечены) равно трем,
следовательно, ранг матрицы
![]() .
.
Находим общее решение однородной системы в координатной форме:
а) Главными
(зависимыми) назовем переменные х1,
х3
и х4,
так как угловые элементы являются
коэффициентами перед х1,
х3
и х4
в ступенчатой
системе, переменная х2
– свободная
(независимая). Свободную переменную
обозначим как
![]() .
.
б) Выпишем ступенчатую систему уравнений, эквивалентную исходной:

в) Выразим
зависимые переменные через свободную
![]() из ступенчатой системы (обратный
ход метода Гаусса),
начиная с последнего уравнения и
подымаясь “вверх” по системе уравнений.
Из третьего уравнения получим:
из ступенчатой системы (обратный
ход метода Гаусса),
начиная с последнего уравнения и
подымаясь “вверх” по системе уравнений.
Из третьего уравнения получим:
![]() .
Из второго уравнения имеем:
.
Из второго уравнения имеем:
![]() .
Из первого уравнения получим:
.
Из первого уравнения получим:
![]() .
.
Формулы
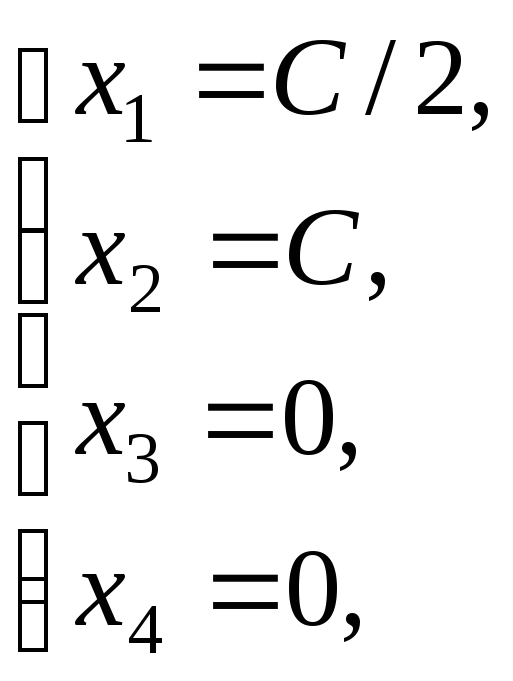
выражающие главные переменные х1, х3 и х4 через свободную переменную (параметры), определяют параметрическую запись решения системы. Эти формулы задают общее решение системы в координатной форме.
Теперь получим
решение однородной системы в векторной
форме. Поскольку ранг матрицы
![]() ,
а размерность системы n=4,
система имеет бесконечное множество
решений. Решения однородной системы
образуют подпространство V
пространства R4
размерности
,
а размерность системы n=4,
система имеет бесконечное множество
решений. Решения однородной системы
образуют подпространство V
пространства R4
размерности
![]() .
.
Базис подпространства
решений однородной системы состоит из
одного вектора
![]() .
Базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
.
Базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
Пусть свободная
переменная принимает значение
![]() ,
получим вектор-решение
,
получим вектор-решение
![]() .
Этот вектор может служить фундаментальной
системой решений однородной системы
уравнений. Тогда любой вектор-решение
.
Этот вектор может служить фундаментальной
системой решений однородной системы
уравнений. Тогда любой вектор-решение
![]() запишется в виде:
запишется в виде:
![]()
где
![]() – произвольная константа. Формула
определяет общее решение однородной
системы
– произвольная константа. Формула
определяет общее решение однородной
системы
![]() в векторном виде.
в векторном виде.
Задача 3. Решить систему (найти общее решение в координатной и векторной форме)
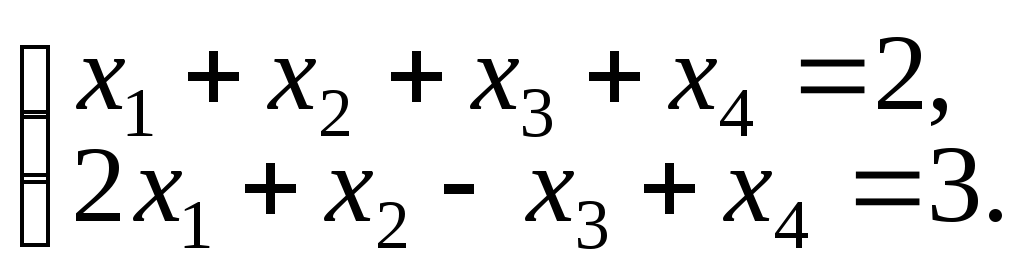
Решение. Расширенная матрица имеет вид:
![]() .
.
Вычитая из 2-й строки 1-ю, умноженную на 2, получаем ступенчатый вид этой матрицы
![]() ,
,
![]() .
.
Следовательно, система совместна: х1, х2 – зависимые переменные, х3, х4 – свободные.
Новая система имеет вид:

Переносим члены со свободными переменными вправо:
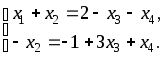
Закончился прямой ход метода Гаусса. Теперь – обратный ход. Из последнего уравнения получаем
![]() .
.
Подставляем в первое:
![]()
откуда
![]() .
.
Итак,
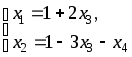
– общее решение в координатной форме неоднородной системы.
Найдем векторную форму. Для этого заменим в общем решении свободные члены нулями:
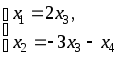
Получаем общее решение однородной системы
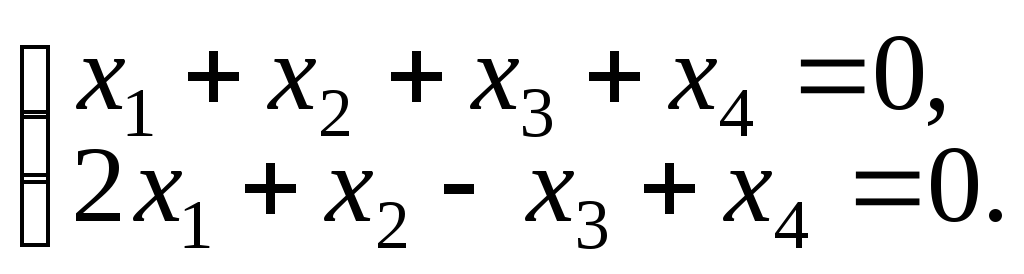
1) Пусть
![]() ,
,
 .
.
2) Пусть
![]() ,
,
 .
.
Следовательно,
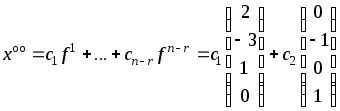 .
.
Найдем частное
решение неоднородной системы. Полагая
в общем решении неоднородной
системы
![]() ,
получаем:
,
получаем:
![]() .
Следовательно,
.
Следовательно,
 .
.
Итак,
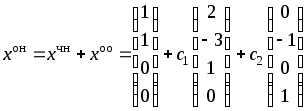
– общее решение в векторной форме.
Задача 4. Решить систему

Решение. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду:
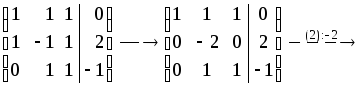
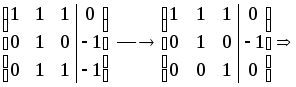

Получили систему ступенчатого вида эквивалентную исходной системе. Все три переменные главные, свободных переменных нет. Решение единственно:
![]() .
.
Задача 5.
Исследовать совместность системы, и в
случае совместности найти общее или
единственное решение системы уравнений
![]() в координатной и векторной формах.
Матрица А
и вектор
в координатной и векторной формах.
Матрица А
и вектор
![]() заданы.
заданы.
 .
.
Решение. Методом Гаусса приведем систему уравнений к ступенчатому виду. Выпишем расширенную матрицу и преобразуем ее:
 .
.
На первом шаге
первую строку не меняем (в верхнем левом
углу стоит ведущий элемент
![]() );
вторую строку не меняем (в первом столбце
стоит
);
вторую строку не меняем (в первом столбце
стоит
![]() нуль); из третьей строки вычитаем первую,
умноженную на 2, и результат запишем в
третью строку; из четвертой строки
вычитаем первую, умноженную на 3, результат
запишем в четвертую строку. Обратите
внимание, что последний столбец меняется
аналогично другим столбцам. Условно
эти операции можно записать так:
нуль); из третьей строки вычитаем первую,
умноженную на 2, и результат запишем в
третью строку; из четвертой строки
вычитаем первую, умноженную на 3, результат
запишем в четвертую строку. Обратите
внимание, что последний столбец меняется
аналогично другим столбцам. Условно
эти операции можно записать так:
![]() .
.
Далее применим
элементарные операции:
![]()
![]() .
Получаем:
.
Получаем:
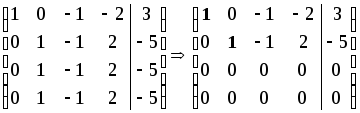 .
.
Угловые элементы (отмечены) определяют, что ранги матрицы системы и расширенной матрицы совпадают:
![]()
по теореме
Кронекера-Капелли система уравнений
совместна, а так как
![]() ,
то система имеет бесконечное множество
решений.
,
то система имеет бесконечное множество
решений.
Закончился прямой ход метода Гаусса. Найдем общее решение системы в координатной форме:
а) Главными
(зависимыми) назовем переменные х1
и х2,
так как угловые элементы являются
коэффициентами перед х1
и х2
в ступенчатой
системе, остальные переменные х3,
х4
– свободные
(независимые). Свободные переменные
обозначим как
![]() ,
,
![]() .
.
б) Выпишем ступенчатую систему уравнений, эквивалентную исходной:

в) Выразим зависимые
переменные через свободные из ступенчатой
системы (обратный ход метода Гаусса),
начиная с последнего уравнения и
подымаясь “вверх” по системе уравнений.
Из второго уравнения получим:
![]() ,
из первого уравнения имеем:
,
из первого уравнения имеем:
![]() .
.
Формулы

выражающие главные
переменные х1,
х2
через свободные переменные (параметры),
определяют параметрическую запись
решения системы. Давая свободным
переменным любые значения и вычисляя
х1
и х2,
получим решение системы
![]() ,
причем любое решение системы можно
получить по этим формулам. Мы нашли
общее
решение системы в координатной форме.
,
причем любое решение системы можно
получить по этим формулам. Мы нашли
общее
решение системы в координатной форме.
Теперь найдем общее решение неоднородной системы в векторной форме. Для этого нужно найти общее решение соответствующей однородной системы и прибавить к нему некоторое частное решение неоднородной системы.
а) Выпишем
соответствующую однородную систему
уравнений
![]() ,
приведенную к ступенчатому виду. Она
только свободными членами отличается
от ступенчатой неоднородной системы
,
приведенную к ступенчатому виду. Она
только свободными членами отличается
от ступенчатой неоднородной системы
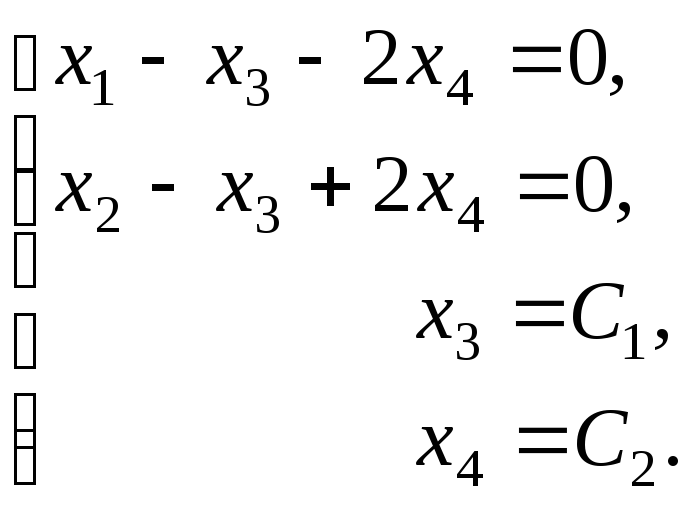
Ранг системы r равен 2, размерность системы n равна 4, система имеет бесконечное множество решений. Решения однородной системы образуют подпространство V пространства R4 размерности
![]() .
.
Базис подпространства
решений однородной системы состоит из
двух векторов
![]() .
Это могут быть любые два линейно
независимые решения системы
.
Это могут быть любые два линейно
независимые решения системы
![]() .
Напомним, что базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
.
Напомним, что базис подпространства V
решений однородной системы называется
фундаментальной
системой решений.
б) Выразим зависимые переменные х1, х2 через независимые х3, х4
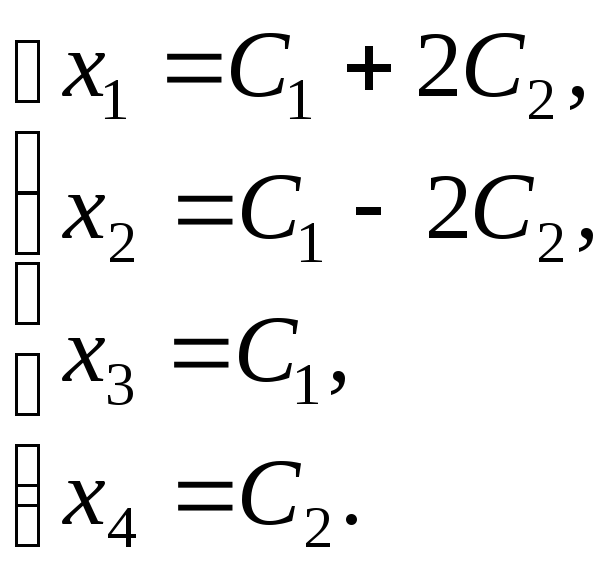
в) Пусть, например,
свободные переменные принимают значения
![]() ,
тогда
,
тогда
![]() ,
получим вектор-решение
,
получим вектор-решение
![]() ;
если
;
если
![]() ,
то получим вектор-решение
,
то получим вектор-решение
![]() .
Пара линейно независимых векторов
.
Пара линейно независимых векторов
![]() может служить фундаментальной системой
решений однородной системы уравнений.
Тогда любой вектор-решение
может служить фундаментальной системой
решений однородной системы уравнений.
Тогда любой вектор-решение
![]() запишется как линейная комбинация
базисных решений:
запишется как линейная комбинация
базисных решений:
![]() ,
,
где
![]() – произвольные константы.
– произвольные константы.
Последняя формула
определяет общее решение однородной
системы
![]() в векторном виде.
в векторном виде.
г) Найдем
какой-нибудь вектор-решение неоднородной
системы
![]() .
Используем для этого параметрическую
(координатную) запись решения неоднородной
системы
.
Используем для этого параметрическую
(координатную) запись решения неоднородной
системы
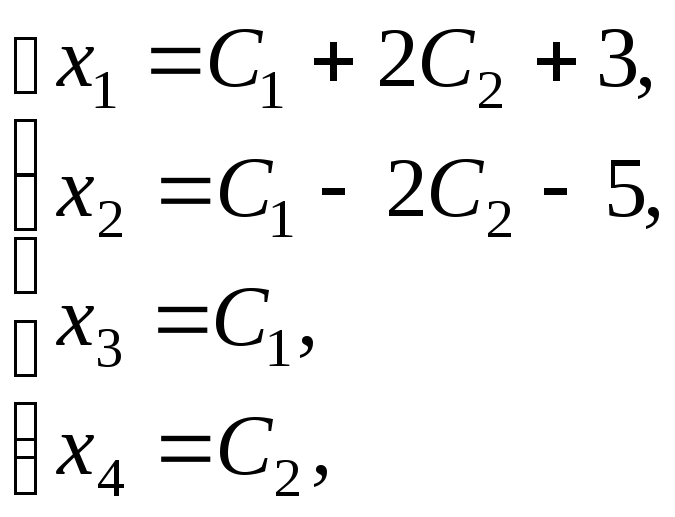
Положим, например,
![]() ,
тогда
,
тогда
![]() .
Вектор
.
Вектор
![]() является некоторым частным решением
неоднородной системы.
является некоторым частным решением
неоднородной системы.
д) Теперь запишем
общее решение
![]() неоднородной системы в виде
неоднородной системы в виде
![]() .
.
Эта последняя
запись является векторной записью
общего решения неоднородной системы
![]() в виде суммы частного решения неоднородной
системы
в виде суммы частного решения неоднородной
системы
![]() и общего решения однородной системы
и общего решения однородной системы
![]() .
.
