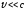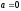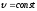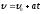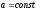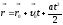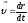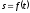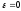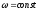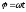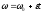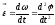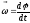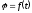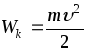Вопросы к экзамену (зачету).

1. Кинематика поступательного движения МТ. Векторный способ описания движения. Радиус-вектора. Путь и перемещение. Скорость и ускорение.

Кинематика изучает движение тел, не рассматривая причины, которые обуславливают это движение, т. е. в ней дается только математическое описание механического движения тел безотносительно к причинам, вызывающих конкретный вид движения.

Кинематика изучает механическое движение тела без рассмотрения причин вызывающих и изменяющих это движение.

Тело отсчета – это тело по отношению к которому определяется положение других тел.

Системой отсчета называется система координат, снабженная часами и жестко связанная с телом отсчета, по отношению к которому определяется положение других тел в различные моменты времени.

Векторный способ описания движения основывается на задании радиус-вектора материальной точки (м.т.).

Радиус-вектор – это вектор, соединяющий начало координат с положением материальной точки в данный момент времени.

Приращение радиус-вектора называется вектором перемещения м.т.

Перемещение – это вектор, соединяющий начальное и конечное положение материальной точки:

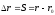
– пройденный путь.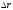

Вектор перемещения направлен вдоль хорды, стягивающей соответствующий участок траектории в случае криволинейного движения.

Скорость.

Скорость определяет быстроту, и направление движения материальной точки в данный момент времени.

Скорость – ВФВ, характеризующая процесс изменения пространственного положения движущейся материальной точки равная перемещению, совершаемому точкой за единицу времени.

Различают:

1) среднюю скорость;

2) мгновенную скорость;

3) среднюю путевую скорость.

Средняя скорость.

Средняя скорость - ВФВ, характеризующая быстроту движения на данном участке и равная отношению приращения радиус-вектора к рассматриваемому промежутку времени Dt: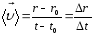

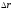
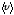
Вектор средней скорости всегда совпадает по направлению с вектором перемещения: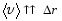

Размерность скорости [u] = 1 м/с

При неограниченном уменьшении промежутка времени Δt средняя скорость стремиться к предельному значению, которое называется мгновенной скоростью.

Мгновенная скорость u – ВФВ, характеризующая быстроту движения в данный момент времени и равная пределу отношения приращения радиус-вектора к бесконечно малому промежутку времени Δt, в течение которого это приращение произошло:

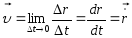
Вектор мгновенной скорости u разложим на три составляющие по координатным осям: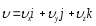

Проекции вектора скорости:

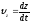
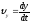
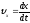
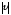
Модуль вектора скорости :

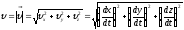
Направление вектора совпадает с направлением вектора элементарного перемещения точки , т. е. он направлен всегда по касательной к траектории.

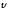
По мере уменьшения Δt путь Δl все больше будет приближаться к , поэтому модуль мгновенной скорости равен первой производной пути по времени: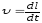

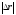
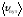
Средняя путевая скорость – СФВ, характеризующая среднюю быстроту изменения со временем пути и равная отношению пройденного пути Δl ко времени Δt, за которое этот путь был пройден: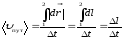

где l – путь, пройденный точкой за время t.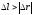

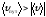
Для криволинейного движения: , т.к.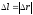

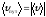
Для прямолинейного движения: ,т.к. .

Ускорение.

Быстроту изменения скорости с течением времени характеризует величина называемая ускорением.

Ускорение – ВФВ, характеризующая процесс изменения скорости с течением времени и равная приращению скорости за единицу времени.

Различают среднее и мгновенное ускорения.

Среднее ускорение.

Среднее ускорение – ВФВ, характеризующая среднюю быстроту изменения скорости м.т. на всем пути и равная отношению приращения скорости к промежутку времени, в течение которого это произошло.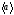

Ускорение имеет размерность [a] = 1 м/с²

Мгновенное ускорение – ВФВ, характеризующая быстроту изменения скорости в данный момент времени и равная пределу отношения приращения скорости к бесконечно малому промежутку времени, в течение которого это приращение произошло: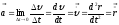

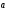
Таким образом, ускорение равно первой производной скорости по времени t, или второй производной радиус-вектора по времени t.

Вектор мгновенного ускорения разложим на три составляющие по координатным осям x, y, z:

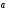
Проекция вектора ускорения на координатные оси:

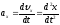
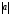
Модуль вектора ускорения :

Вывод: определение скорости и ускорения сводится к чисто математической задаче вычисления первой и второй производных по времени радиуса вектора этой точки.

Кинематика поступательного движения твердого тела МТ.

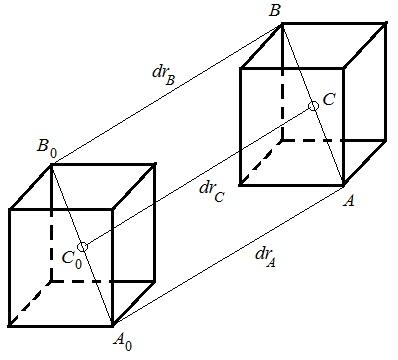
Поступательное движение является простейшим видом механического движения твердого тела, при котором прямая, соединяющая любые две точки этого тела, перемещаясь вместе с телом, остается параллельной своему первоначальному направлению.

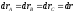
Где - радиусы-векторы точек А, В, С и произвольной точки М тела.

Следовательно,

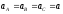
Вывод: из этих соотношений следует, что для кинематического описания поступательного движения твердого тела и МТ достаточно рассмотреть движение какой либо одной его точки.

2. Координатный и естественный способы описания движения. Проекция. Тангенциальное и нормальное ускорение.

Координатный способ.

Координатный способ задает положение тела в пространстве с помощью координат тела.

Переход от векторного описания движения к координатному осуществляется путем проектирования.

Проекции радиус-вектора на координатные оси равны соответствующим координатам м.т.:

r_x = x; r_y = y; r_z = z.

Обратный переход осуществляется с помощью теоремы Пифагора и направляющих косинусов: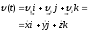

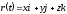
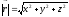
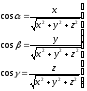
Направляющие косинусы:

Числом степеней свободы называется число независимых координат, полностью определяющих положение точки (тела) в пространстве относительно выбранной системы отсчета.

Законом движения материальной точки называется уравнение, выражающее зависимость ее радиуса-вектора от времени: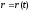

Спроектировав данное уравнение на оси координат, тогда зададим движение тела в прямоугольной (декартовой) системе координат:

Данные уравнения кинематическими уравнениями движения материальной точки.

Траекторией называется линия, которую описывает материальная точка при своем движении относительно выбранной системы отсчет.

Естественный способ описания движения.

В основу естественного способа описания движения положено уравнение траектории или пути, проходимого телом.

Естественный способ описания движения позволяет «привязать» описание движения к его траектории. В основе этого способа лежит естественная тройка векторов – вектор тангенциали , вектор нормали и вектор бинормали .

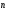
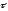
Вектор тангенциали - это вектор, касательный к траектории в данной точке.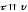

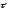
Вектор нормали - это вектор, направленный из данной точки к центру кривизны траектории.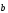

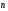
Вектор бинормали - это вектор, являющиеся векторным произведением тангенциали и вектора нормали .

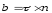
Векторы , , образуют правовинтовую систему. Она также является правой прямоугольной (декартовой) системой координат.

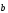
Если , то векторы станут ортами соответствующих осях.

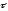
Скорость точки при естественном способе описания движения.

Движение точки задано естественным способом, т. е. известна траектория точки и закон ее движения по этой траектории . Вычислим скорость этой точки.

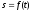
Воспользуемся определением скорости: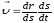

Правую часть до множим и разделим на ds. Получим:

Где - модуль скорости движущейся точки.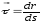

-единичный вектор тангенциали, направлен по касательной к траектории в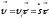

данной точке. Запишем:

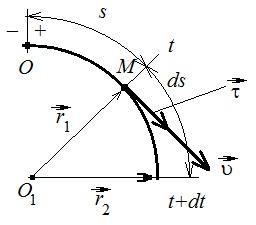
Ускорение точки при естественном способе описания движения.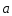

Траектория точки – плоская кривая, то ускорение точки лежит в данной плоскости.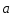

Вектор полного ускорения удобно разложить на две составляющие вдоль этих направлений:

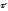
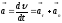
У плоскости имеются два направления – касательное к траектории (вектор тангенциали ) и главной нормали (вектор нормали ).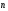

-называется тангенциальным ускорением;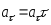

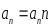
-называется нормальным ускорением (центростремительным ускорением) ;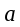

-называется вектором полного ускорения.

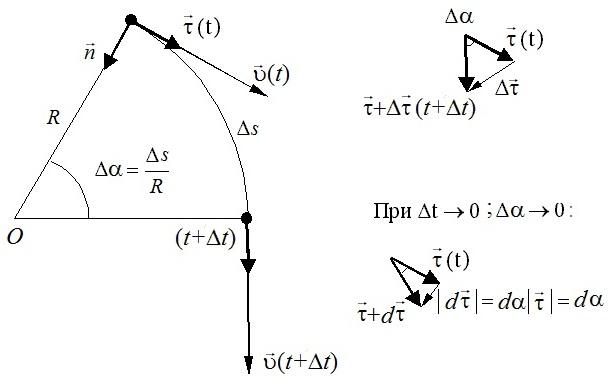
Ввиду малости этого участка траектории его можно считать совпадающим с соответствующим участком соприкасающейся окружности радиусом R с центром в точке О, которому соответствует центральный угол: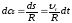

При перемещении по траектории на малое расстояние ds единичный вектор касательной поворачивается на угол dα.

Ввиду малости dα следует:

По направлением вектор совпадает с единичным вектором главной нормали .

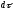
Таким образом,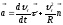

Для полного ускорения уравнение можно записать в виде:

Для нахождения тангенциального и нормального ускорения воспользуемся формулой для скорости при естественном способе описании движения точки: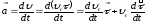

Следовательно,

Где -приращение орта касательной к траектории, соответствующее элементарному пути проходимому точкой.

Модуль полного ускорения точки рассчитывается по формуле:

При криволинейном движении точки вектора его полного ускорения всегда отклонен от касательной траектории в сторону ее вогнутости.

Движение точки можно классифицировать в зависимости от тангенциальной и нормальной составляющих ускорения следующим образом: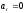

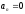
1. И - движение прямолинейное равномерное;

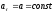
2. И - движение прямолинейное равнопеременное;

3. И - движение прямолинейное с переменным ускорением;

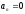
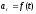
4. И - движение по окружности с постоянной скорости;

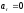
5. И - движение равномерное криволинейное;

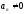
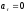
6. И - движение равнопеременное криволинейное;

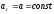
7. И - движение криволинейное с переменным ускорением.

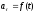
3.Кинематика вращательного движения МТ. Угловые характеристики движения. Связь между линейными и угловыми величинами.

Кинематика вращательного движения твердого тела и МТ .

А)Вращательным движением твердого тела называется движение, при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Ось вращения может проходить как через вращающееся тело, так и находиться вне этого тела.

Вращающееся тело имеет одну степень свободы вокруг неподвижной оси.

Положение тела в пространстве определяется значением угла поворота вокруг оси вращения.

Б) Угловое перемещение.

Рассмотрим вращение м.т. по окружности радиуса R.

Пусть в начальный момент времени t₀ м.т. находится в положении M и ее скорость равна u₀.

Спустя промежуток времени dt = t₁ – t₀ м.т. пройдет по окружности путь l и окажется в положении M₁.

Радиус-вектор точки, проведенный из центра O окружности, повернется на угол j.

Угол j называется угловым путем (углом поворота).

Размерность углового пути [j] = 1 рад.

Из геометрии известно, что длина дуги, на которую опирается центральный угол MOM₁, равна: l = jR

Положение тела в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного начального положения этого тела.

Для описания вращательного движения тела неудобно пользоваться понятиями кинематики, как: перемещение; пройденный путь; скорость и ускорение.

В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела .

По модулю вектор элементарного угла поворота равен углу dφ поворота тела вокруг его оси вращения за время dt и направлен вдоль этой оси по правилу правого винта (правилу буравчика).

В) Правило правого винта (правило буравчика):

Если вращательное движение буравчика с правой нарезкой совпадает с направлением вращения, то поступательное движение острия буравчика укажет направление вектора элементарного угла поворота (вектора углового перемещения).

Направление вращения м.т. по окружности задается с помощью вектора углового перемещения .

Модуль вектора углового перемещения равен угловому пути j м.т. , а направление вектора углового перемещения подчиняется правилу буравчика.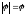

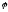
Угловой путь j и модуль вектора углового перемещения измеряются в радианах.

При вращательном движении наряду с линейными величинами вводят угловые величины.

К ним относят: угловой путь j, угловое перемещение , угловую скорость , угловое ускорение и др.

Большинство из векторных угловых величин относятся к классу аксиальных (axe (лат.) – ось) векторов.

Аксиальные векторы (псевдовекторы) – это векторы, характеризующие вращение.

В отличие от полярных векторов аксиальные вектора всегда направлены вдоль оси вращения и не имеют конкретной точки приложения. При переходе от правой системы координат к левой псевдовектора изменяют свое направление на противоположное.

Полярные вектора при переходе от правой системы координат к левой всегда сохраняют свое направление неизменным.

Векторное произведение двух полярных векторов дают псевдовектор.

Аксиальные векторы могут быть отложены от любой точки на оси вращения.

Угловая скорость.

Угловая скорость – ВФВ, характеризующая быстроту поворота и равная пределу отношения приращения вектора углового перемещения к бесконечно малому промежутку времени, в течение которого это приращение произошло: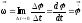

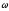
Размерность угловой скорости [w] = 1 рад/с

Угловая скорость является псевдовектором (аксиальным вектором) как и угловое перемещение.

Угловая скорость направлена вдоль оси вращения и ее направление всегда совпадает с направлением вектора углового перемещения

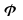
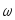
Направление вектора угловой скорости определяется правилом правого винта (правилом буравчика).

Вращение тела вокруг неподвижной оси называется равномерным, если модуль угловой скорости постоянен: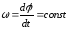

В случае равномерного вращения угол поворота тела прямо пропорционален времени его вращения t: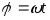

При равномерном вращении угловая скорость ω показывает, на какой угол поворачивается тело за единицу времени.

Для характеристики равномерного вращения вводятся две величины – период T обращения и частота n обращения.

Период T обращения – это время за которое тело делает один полный оборот.

Размерность периода обращения [T ] = 1 с

Найдем связь периода T обращения с угловой скоростью.

Величина равная обратной величиной периода вращения (обращения) называется частотой вращения или числом оборотом в единицу времени.

Частота n обращения – это число оборотов совершаемое телом за единицу времени, равномерно вращающегося с угловой скоростью .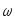

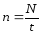
Размерность частоты обращения [n] = 1 с^-1

Частота n обращения обратно периоду T обращения: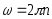

Угловая скорость связана с частотой обращения по формуле:

Угловое ускорение.

Угловое ускорение – ВФВ, характеризующая быстроту изменения вектора угловой скорости и равная пределу отношения приращения вектора угловой скорости к бесконечно малому промежутку времени , в течение которого произошло приращение скорости: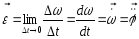

Угловое ускорение является псевдовектором (аксиальным вектором) как угловая скорость и угловое перемещение.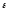

Размерность углового ускорения [e ] = 1 рад/с².

Вектор углового ускорения может принимать всего два направления: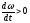

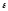
1. Если (ускоренное вращение), то

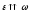
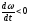
2. Если (замедленное вращение), то

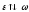
Связь между линейными и угловыми величинами.

Найдем скорость υ произвольной точки N тела.

Радиус-вектор точки N равен:

Перемещаясь по дуге окружности точка N проходит путь: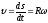

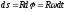
Модуль скорости точки N:

Учитывая, векторы R и ω взаимно перпендикулярны и вектор скорости υ точки N направлен перпендикулярно обоим этим векторам, можем написать:

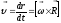
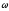
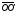
Так как векторы и коллинеарные, тогда формулу можно переписать в виде:

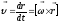
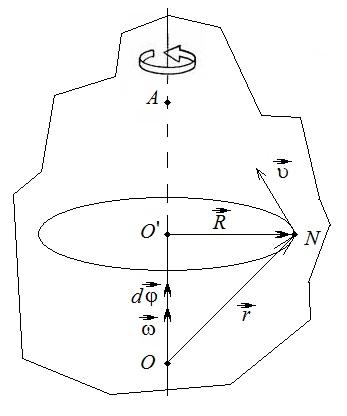
В отличие от угловой скорости тела ω скорость υ часто называют линейной скоростью точки N тела. Вектор υ направлен по правилу правого винта.

Найдем ускорение точки N тела вращающегося вокруг неподвижной оси.

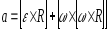
Или

Первый член в правой части этой формулы представляет собой касательное (тангенциальное) ускорение а_τ точки N: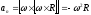

второй – нормальное ускорение а_n точки N:

Минус в последней формуле стоит потому, что векторы а_n и R имеют противоположные направления.

В более общем виде эти выражения можно записать в векторном виде:

здесь - радиус-вектор м.т., проведенный из центра окружности. Его модуль равен радиусу вращения:

Выразим полное ускорение точки через угловые величины.

название	Равномерное движение	Равнопеременное движение	Неравномерное движение
Поступательное движение
Вращательное движение

4.Прямолинейное равномерное движение. Прямолинейное равнопеременное движение.

Прямолинейное движение – это механическое движение, при котором вектор перемещение не меняется по направлению и по величине длине пути пройденного телом.

Равномерным движением называется движение, при котором за любые равные промежутки времени точка проходит одинаковые расстояния, при этом ее вектор скорости не изменяется по величине и он не меняет своего направления.

Скорость постоянная, т. е.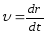

Последнюю формулу проинтегрируем:

Получим уравнение равномерного движения: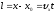

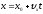
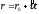
Равномерное прямолинейное движение

График скорости

График движения

Равнопеременным движением называют такое движение по траектории любой формы, при котором касательное ускорение является величиной постоянной

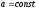
Получим уравнение для равнопеременного движения и формулу для мгновенной скорости.

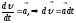
Получим формулу скорости. Воспользуемся определением ускорения:

Последнюю формулу проинтегрируем:

Проекция на ось ОХ имеет вид:

Получим уравнение равнопеременного движения. Воспользуемся определением скорости:

Так как то с учетом получим: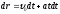

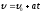
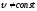
Последнюю формулу проинтегрируем: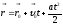

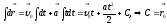
Проекция на ось ОХ имеет вид:

Равнопеременное прямолинейное движение.

График скорости.

График движения.

График ускорения.

5. Законы Ньютона.

Инерциальные системы отсчета. Сила, масса и импульс тела. Первый закон Ньютона.

Динамика изучает механическое воздействие тел с учетом вызвавших его причин.

Динамику интересуют силы, действующие на тела.

Сила – ВФВ, характеризующая механическое воздействие тел и полей.

О действии сил можно судить по двум признакам:

1. Появление ускорение (динамическое действие);

2. Деформация тел (статическое действие).

Принцип суперпозиции для сил:

Если на тело действуют несколько сил, то силы действуют независимо друг от друга, и результат их действия складывается по правилам действия над векторами.

Равнодействующая (результирующая) сила – это сила, оказывающая на тело такое же действие, что и данные силы вместе:

Инерциальная система отсчета (ИСО) – это система отсчета, связанная со свободным невращающимся телом.

Свободным называется тело, не взаимодействующее с другими телами.

Первый закон Ньютона (закон инерции).

Первый закон Ньютона говорит о движении свободной м.т. относительно ИСО.

Формулировки первого закона Ньютона:

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2. Существуют такие системы отсчета, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела (или действия других тел компенсируются).

3. В ИСО свободная м.т. либо покоится либо движется равномерно и прямолинейно.

Инерция- это явление сохранения скорости тела по модулю и направлению до тех пор, пока на него не подействуют другие тела.

Инертность – свойство тел, проявляющееся в том, что скорость тела изменяется не мгновенно, а с течением времени.

Масса тела m – СФВ, являющаяся мерой инертных свойств тела при его поступательном движении и мерой гравитационных свойств тела.

[m] = 1 кг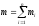

Свойство аддитивности массы:

Импульс (количество движения) м.т.- ВФВ, являющаяся мерой ее механического движения и равная произведению m массы материальной точки на вектор скорости: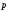

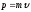
Второй закон Ньютона(основной закон динамики).

Второй закон Ньютона отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.

Ускорение, приобретаемое м.т. В ИСО, прямо пропорционально силе, действующей на нее, и обратно пропорционально ее массе:

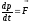
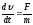
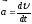
Скорость изменения импульса тела равна равнодействующей всех сил, приложенных телу ( более общая формулировка второго закона Ньютона).

Выражение (1) не выполняется в тех случаях, когда масса тела изменяется.

Выражение (2) является универсальным.

Второй закон Ньютона справедлив только в инерциальных системах отсчета.

В случае равенства нулю равнодействующих сил ускорение также равно нулю, т.е. этот вывод совпадает с утверждением Первого закона Ньютона.

Первый закон Ньютона рассматривается как самостоятельный закон (а не как следствие второго закона), так как именно 1-ый закон утверждает существование инерциальных системах отсчета, в которых выполняется 2-ой закон Ньютона.

В механике выполняется принцип независимости действия сил: если на м.т. действуют одновременно несколько сил, то каждая из этих сил сообщает м.т. ускорение согласно 2-му закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускорение можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач.

Третий закон Ньютона.

В современной физике различают четыре вида взаимодействий:

1) гравитационное (взаимодействие обусловленное всемирным тяготением);

2) электромагнитное (осуществляемое через электрическиие и магнитные поля);

3) Сильное или ядерное (обеспечивающее связь частиц в атомном ядре);

4) слабое (ответственное за многие процессы распада элементарных частиц).

В рамках классической механики имеют дело с гравитационными и электромагнитными силами, а также с силами упругости и трения, вес тела, силой реакцией опоры.

Гравитационные и электромагнитные силы являются фундаментальными – их нельзя свести к другим, более простым, силам.

Законы фундаментальных сил просты и выражаются точными формулами. Пример:

Гравитационная постоянная:

Силы упругости, сила трения, вес тела, сила реакции опоры являются по своей природе электромагнитными и, следовательно, не могут считаться фундаментальными. Для этих сил можно получить лишь приближенные эмпирические (опытные) формулы. Примеры: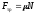

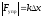
6. Механическая система. Работа силы. Мощность.

Механическая система.

Механической системой называется мысленно выделенная совокупность тел рассматриваемых в конкретной задаче, которые играют в ней существенную роль.

Внешние тела – это тела которые не вошли в рассматриваемую механическую систему, их еще называют внешней средой.

Механические системы бывают: замкнутыми и открытыми.

Замкнутой механической системой называется система, на которую не действуют внешние силы.

Открытой механической системой называется система на которую действуют внешние силы.

Механическая система- это совокупность материальных точек (тел), рассматриваемых в данной механической задаче.

В механических системах различают внутренние и внешние силы.

Сумма всех внутренних сил в механической системе всегда равно нулю:

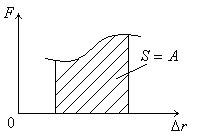
Работа силы.

Работа A силы – СФВ, характеризующая процесс передачи механического движения от одного тела к другому и равная скалярному произведению вектора силы на вектор перемещения:

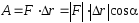
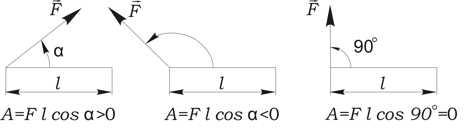
[A] = 1 Н·м = 1 Дж (джоуль)

Элементарная работа:

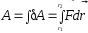
Мощность силы.

Мощность N (P) силы – СФВ, характеризующая быстроту совершения работы и равная производной работы по времени:

Средняя мощность

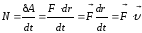
7. Энергия. Кинетическая и потенциальная энергия.

Энергия.

Энергия – это универсальная и наиболее общая характеристика всех форм движения материи и их превращений друг в друга.

Энергией называется СФВ изменение, которой равна работе совершаемой в данном процессе.

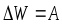
Для различных форм движения и соответствующих им взаимодействий в физике рассматривают следующие виды энергии: механическую; внутреннюю; электромагнитную; ядерную и т.д.

В механике рассматривается механическая энергия.

Механическая энергия тела – СФВ, являющаяся мерой его механического движения и механического взаимодействия и зависящая от массы тела, скорости его движения и расстояния до других тел или расстояния между частицами одного и того же тела.

Для количественного описания механического движения тела, при котором происходит изменение энергии тела, в механике вводят понятие работы силы.

В механике различают два вида механической энергии: кинетическую и потенциальную.

Кинетическая энергия.

Кинетической энергией механической системы называется энергия механического движения этой системы.

Изменение кинетической энергии м.т. происходит под действием приложенной к ней силы F и равно работе совершаемой этой силой.

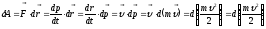
Кинетическая энергия W_k тела - СФВ, являющаяся мерой его механического движения и равная половине произведения массы частицы на квадрат ее скорости, т.е.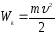

Теорема о кинетической энергией.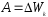

Кинетическая энергия механической системы равна сумме кинетических энергий всех частей этой системы: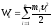

Кинетическую энергию твердого тела движущегося поступательно можно найти по формуле: m-масса всего тела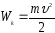

Кинетическая энергия системы есть функция состояния ее механического движения f(υ), т.е. она полностью определяется значением масс и скоростей входящих в неё тел (материальной точки.).

Кинетическая энергия системы в отличии от её импульса не зависит от того, в каких направлениях движутся её части (тела или м.т. входящие в рассматриваемую механическую систему).

Потенциальная энергия.

Потенциальная энергия - СФВ, являющаяся мерой механического взаимодействия тел или частей тела и является непрерывной однозначной и дифференцируемой функцией, зависящей от расстояния между телами или расстояния между частицами одного тела.

Потенциальная энергия тела в гравитационном поле.

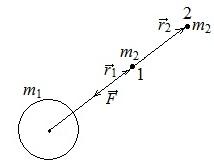
Потенциальная энергия тела в гравитационном поле:

при r → ∞ W_p → 0

Значение потенциальной энергии можно определить с точностью до некоторой постоянной, поэтому выбор начал отсчета условен.

Обычно за нулевой уровень энергии принимают потенциальную энергию бесконечности.

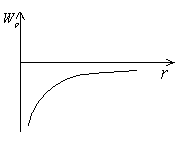
Потенциальная энергия тела, поднятого над Землей.

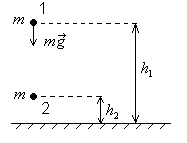F_тяж = const

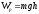
Потенциальная энергия тела поднятого над землей (при h << R_З):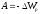

Теорема потенциальной энергии:

Работа внешних консервативных сил равна убыли потенциальной энергии тела.

Потенциальная энергия упруго деформированного тела.

Воспользуемся законом Гука: F_уx = - kx = - kr_x

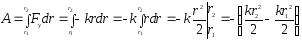
Заменим r₁ и r₂ на x₁ и x₂ соответственно: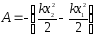

Согласно теореме о потенциальной энергии: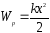

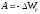
Потенциальная энергия упругого деформированного тела:

Согласно закону Гука F_у = kDl. Построим график:

Учтем, что F_у является переменной силой.

A = -DW_p = W_p0 - W_p = - W_p

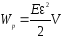
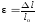
С учетом того, что и V = Sl₀, имеем

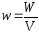
Объемная плотность энергии тела:

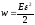
Объемная плотность энергии упруго деформированного тела:

Связь консервативной силы и потенциальной энергии.

Применим теорему о потенциальной энергии к элементарной работе консервативной силы: dA = -dW_p,

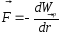
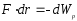
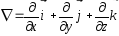
Оператор Гамильтона (набла-оператор):

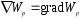
Вектор градиента скалярного поля – это вектор, показывающий направление наибольшего возрастания данной скалярной функции и равный производной данной функции по координатам.

Связь между консервативной силой и потенциальной энергии:

8. Законы Кеплера. Закон всемирного тяготения. Сила тяжести. Вес тела. Ускорение свободного падения.

Законы Кеплера.

1. Первый закон Кеплера: все планеты Солнечной системы обращаются по эллипсам, в одном из фокусов которых находится Солнце.

2. Второй закон Кеплера: все планеты Солнечной системы движутся с постоянными секторными скоростями, т.е. радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.

3. Третий закон Кеплера: квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей их орбит.

Закон всемирного тяготения.

Закон всемирного тяготения (1687 г.):

Сила гравитационного притяжения двух материальных точек прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:

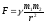
• гравитационная постоянная

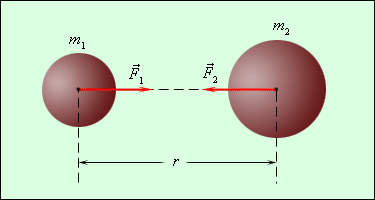
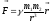
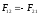
Границы применимости:

1. для точечных масс.

2. для удаленных тел

3. для сферических тел с равномерным распределением плотности по слоям.

Сила тяжести.

Сила тяжести тела – это отвесная составляющая силы земного тяготения, действующей на тело.

-сила гравитационного притяжения.

-сила натяжение нити.

j - географическая широта местности.

По теореме косинуса:

1. полюс (j=90°) F_тяж = F_г

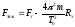
2. экватор (j=0°)

3. Максимальное различие между F_тяж и F_г не превышает 0,3% Þ Будем считать F_тяж » F_г

Ускорение свободного падения.

Ускорение свободного падения – это ускорение, придаваемое телу в вакууме силой тяжести, то есть геометрической суммой гравитационного притяжения планеты (или другого астрономического тела) и инерциальных сил, вызванных её вращением.

Пусть тело находится на поверхности Земли (r = R_з):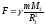

F = ma

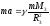
1. Ускорение свободного падения на поверхности Земли:

2. Ускорение свободного падения на высоте h над поверхностью Земли:

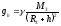
g зависит от:

1. высота;

2. географической широты;

3. залегания горных пород.

Вес тела.

Вес тела - это сила, воздействия тела на опору (или другой вид крепления в случае подвешенных тел), препятствующую падению, возникающая в поле сил тяжести или подвеса.

Вес тела – сила, с которой тело давит на опору или натягивает подвес вследствие гравитационного притяжения к Земле.

Нормальная реакция опоры – сила, с которой опора действует на тело в направлении, перпендикулярном к поверхности соприкосновения тела и опоры.

Вес тела и сила реакции опоры равны по третьему закону Ньютона:

В современной науке вес и масса — совершенно разные понятия: масса является неотъемлемым свойством тела, а вес — результат действия силы тяжести на опору.

Во многих повседневных ситуациях слово «вес» продолжает использоваться, когда фактически речь идет о «массе».

[m] = 1 кг

[P] = 1 Н

Сила реакции опора (реакция подвеса) – это сила, с которой опора и подвес действует на тело.

9. Космические скорости. Гравитационное поле.

Космические скорости:

1. Первая космическая скорость- это скорость, которую необходимо сообщить телу, чтобы оно стало искусственным спутником Земли.

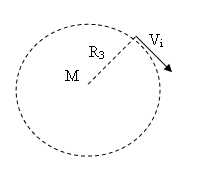
2. Вторая космическая (параболическая) скорость – это скорость, которую необходимо сообщить телу, чтобы оно покинуло пределы Земли и стало спутником Солнца.

W_k1 + W_p1 = W_k2 + W_p2 - ЗСЭ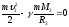

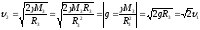
3. Третья космическая скорость – это скорость, которую необходимо сообщить телу для того, чтобы оно покинуло пределы Солнечной системы.

u₃ = 16,7 км/с, если тело запускать по ходу орбитального движения Земли

Гравитационное поле.

Гравитационное поле – это физическое поле, через которого осуществляется гравитационное воздействие.

По современным представлениям любое силовое взаимодействие передается с помощью поля.

Гравитационное взаимодействие осуществляется гравитационным полем.

Напряженность гравитационного поля.

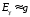
Потенциал гравитационного поля.

Силовая линия поля – это линия, в каждой точке которой вектор напряженности направлен по касательной к ней.

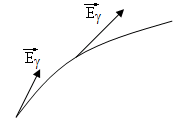
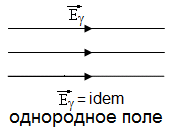
10. Силы упругости. Виды деформации. Закон Гука. Диаграмма растяжения. Механический гистерезис.

Силы упругости.

Упругая сила – это сила, возникающая в теле при его упругой деформации.

Силы упругости по своей природе относятся к электромагнитному виду взаимодействия.

Деформация тела – это изменение его формы и размеров под действием внешних сил.

Деформация:

1. упругие (полностью исчезает после снятия внешней нагрузки);

2. пластичные (сохраняется при снятие внешней нагрузки).

Закон Гука.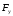

Сила упругости , возникающая в теле, пропорциональна удлинению тела.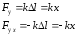

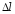
x = Dl = l – l₀ - абсолютное удлинение тела

k - коэффициент упругости (жесткость) тела

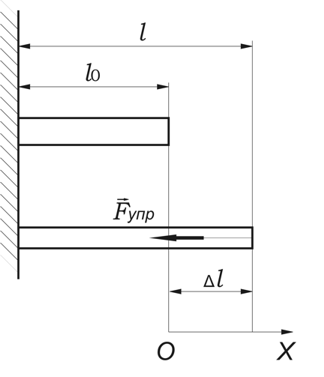
Виды деформации:

1. растяжения и сжатие;

2. кручение;

3. сдвиг;

4. изгиб.

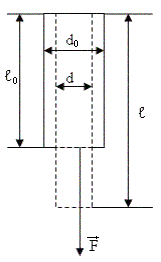
Деформация растяжения (сжатия).

Dl = l – l₀ – абсолютное продольное удлинение,

Dd = d – d₀ – абсолютное поперечное сжатие,

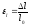
- относительное продольное удлинение,

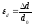
- относительное поперечное сжатие,

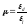
- коэффициент Пуассона, m £ 0,5

Механическое напряжение s – СФВ, характеризующая распределение упругой силы по сечению образца и равная:

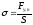
- механическое усиление,

[s] = [p] = 1 Н/м² = 1 Па (паскаль)

В случае упругих деформаций однородных тел:

s = p, т.к. F_у = F_внеш

Закон Гука: Механическое напряжение, возникающее в теле, прямо пропорционально его относительному удлинению (сжатию):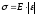

E - модуль Юнга [E] = 1 Н/м² = 1 Па

Модуль Юнга равен такому нормальному механическому напряжению, возникающему в теле, при котором относительное удлинение было бы равно единице, следовательно, приращение длины было бы равно первоначальной длине стержня, т.е. оно изменило свои размеры в два раза.

Физический смысл модуля Юнга:

E = s, если

l – l₀ = l₀

l = 2l₀

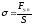
Нормальное механическое напряжение:

Относительное продольное удлинение: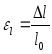

Деформация кручения.

ϕ - угол закручивания диаметра нижнего основания цилиндра;

L – высота цилиндра;

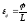
- относительная деформация кручения;

M = Cj - момент силы кручения;

C = const - постоянная кручения.

Деформация сдвига.

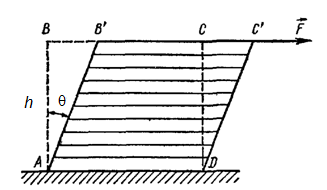
Dx = CC¢ - абсолютный сдвиг.

γ - относительный сдвиг, [γ] = 1 рад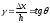

Для малых деформаций (θ → 0):

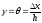
tgq » q Þ

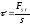
Тангенциальное механическое напряжение: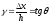

Относительный сдвиг:

Закон Гука: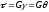

G - модуль сдвига

[G] = 1 Н/м² = 1 Па

Модуль сдвига равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равен 45°, т.е.

Деформация изгиба.

Dh = CC₁ - стрела прогиба

Механический гистерезис.

Неоднозначность деформации при одной и той же величине напряжения при нагружение и разгрузке. Не совпадающие линии нагружения и разгрузки на диаграмме «напряжение – деформация» образуют петлю гистерезиса.

Гистерезис называют упругим, если площадь петли гистерезиса изменяются приблизительно пропорционально напряжению, и пластическим, если сравнительно малое изменение этого напряжения вызывает значительное изменение площади петли. Последняя зависит от типа напряженного состояния: при кручении и изгибе она больше, чем при растяжении и сжатии.

С повышением температуры металлов увеличивается площадь петли. Исключение составляет зона хладноломкости( переход металла из всякого в хрупкое состояние ), при которой обнаруживаются более узкие петли гистерезиса. Наклеп увеличивает площадь петли, скорость деформации уменьшает. Петля гистерезиса характеризует способность материала поглощать энергию при колебании конструкций. Чем больше площадь петли, тем больше энергия, рассеянная в материале, и тем быстрее затухают колебания. Рассеянную энергию деформации, эквивалентную площадь петли, учитывают при расчете затухающих колебаний.

Диаграмма растяжения.

11. Сила трения.

Сила трения.

Силы трения возникают (проявляются) при перемещении соприкасающихся тел или их частей друг относительно друга.

Трение – взаимодействие между соприкасающимися телами, препятствующее их относительному движению.

Сила трения относится к электромагнитному виду взаимодействия.

Трение возникающее при относительном перемещении двух соприкасающихся тел, называют внешним трением, а трение между частями одного и того же сплошного тела (например жидкости или газа) называют внутренним трением.

Внешнее (сухое) трение – трение между поверхностями твердых тел.

Внутренне (вязкое) трение – трение между движущимися слоями жидкости или газа.

Внешнее трение:

1. трение покоя;

2. трение скольжения;

3. трение качения.

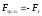
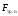
- сила трения покоя.

[ m_п] = 1

F_тр.п.max = m_пN –закон Амонтона-Кулона

m_п - коэффициент трения покоя, [m] = 1

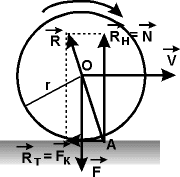
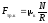
• сила трения качания.

m_к - коэффициент трения качения, [m_к] = 1 м

Коэффициент трения зависит от материала соприкасающихся поверхностей, качества их обработки и физического состояния, но не зависит от их площади.

Если соприкасающиеся тела в различных случаях изготовлены из одних и тех же материалов, то выполняется следующее соотношение между модулями сил трения:

F_тр.к < F_тр < F_тр.п.max

12. Момент импульса тела. Момент силы. Закон сохранения момента импульса тела.

Момент импульса тела.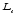

Моментом импульса м.т. А относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением радиуса-вектора м.т., проведенного из точки О, на импульс этой материальной точки :

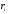
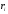
- радиус-вектор, пройденный из точки О в точку А;

- импульс материальной точки.

Момент импульса является псевдовектором, его направление совпадает с направлением правого винта при его вращении от к .

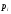
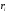
Модуль вектора момента импульса: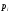

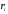
α – угол между векторами и .

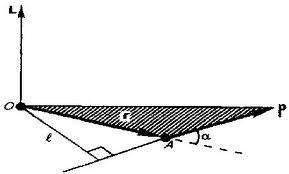
При вращении абсолютно твердого тела вокруг неподвижной оси момент импульса отдельной м.т. равен: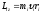

и направлен по оси в сторону, определяемую правилом правого винта.

Моментом импульса механической системы относительно неподвижной точки О называется вектор , равный геометрической сумме моментов импульса относительно той же точки О всех м.т. механической системы: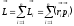

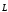
Моментом импульса твердого тела относительно неподвижной оси ОZ, есть сумма моментов импульса всех м.т. из которых состоит это тела и равен: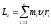

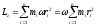
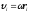
С учетом, что получим:

Момент силы.

Моментом силы М относительно неподвижной точки О называется векторная физическая величина, определяемая векторным произведением радиуса вектора r, проведенного из точки О в точку А приложения силы , на силу F:

Момент силы является псевдовектором, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Вектор направлен перпендикулярно плоскости образованной векторами r и F.

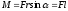
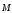
Модель момент силы:

α – угол между векторами r и F;

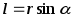
- плечо силы F, кратчайшее расстояние между линией действия силы и точкой О, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.

Моментом силы М относительно неподвижной оси OZ называется скалярная величина М_Z, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки. О находящейся на данной оси OZ.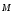

Значение момента M_Z не зависит от выбора положения точки О на оси OZ.

Если ось OZ совпадает с направлением вектора , то момент силы представляется в виде вектора, совпадающего с осью: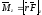

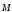
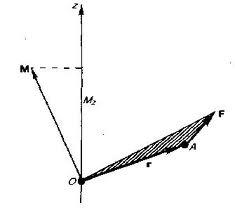
Закон сохранения момента импульса.

Для замкнутой системы момент внешних сил М^внеш всегда равен нулю, так как на нее внешние силы не действуют.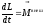

Из основного закона динамики вращательного движения твердого тела:

Вытекает закон сохранения момента импульса: момент импульса замкнутой системы относительно неподвижной точки (оси) не изменяется с течением времени.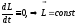

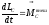
Из уравнения следует:

момент импульса замкнутой системы относительно ее центра масс не изменяется с течением времени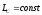

Момент импульса замкнутой системы относительно любой неподвижной оси а также остается постоянным:

Закон сохранения момента импульса является фундаментальным законом природы, который далеко выходит за рамки классической механики.

Закон сохранения момента импульса связан со свойством симметрии пространства – его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.

Моментом импульса обладают не только движущиеся макроскопические тела и системы, но также и отдельные атомы, атомные ядра и элементарные частицы.

Атомные ядра имеют моменты импульса, не связанные с их движением в пространстве.

13. Теорема о движении центра масс. Закон сохранения импульса тела.

Теорема о движении центра масс.

Центр масс механической системы – это точка масса которой равна массе системы, а радиус вектор задается уравнением: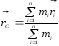

или в скалярной форме трех уравнений

Центром масс или центром системы материальных точек называется точка. С радиус-вектор которой равен отношению суммы произведений масс всех материальных точек системы на их радиусы векторы к массе всей системы.

Вокруг центра масс уплотнилась бы механическая система, если бы силы гравитационного притяжения возросли до бесконечности.

m₂ > m₁

Замкнутая механическая система – система, на которую не действуют внешние силы.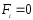

Квазизамкнутая механическая система – система, на которую действуют скомпенсированные внешние силы.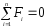

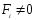
Незамкнутая механическая система – система, на которую действуют не скомпенсированные внешние силы.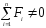

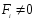
Продифференцируем радиус-вектор центра масс и найдем скорость ее движения: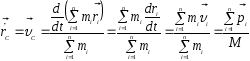

Теорема о движении центра масс:

Центр масс механической системы движется как точка, масса которой равна массе всей системы. Импульс системы равен импульсу центра ее масс.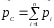

Закон сохранения импульса (ЗСИ).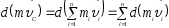

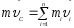
Закон о движении центра масс: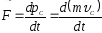

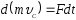
Импульс силы:

Если система замкнута, то , тогда

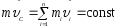
Закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени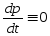

Закон сохранения импульса:

Геометрическая сумма импульсов тел замкнутой механической системы не изменяется.

Хотя ЗСИ получен с помощью законов динамики, он не является их следствием.

Все законы сохранения являются универсальными, т.е. выполняются и в макромире и в микромире.

Согласно теореме Эмми Нётер (1918 г.) каждому свойству симметрии физической системы соответствует некоторый закон сохранения.

Закон сохранения импульса – следствие однородности пространства.

14. Реактивное движение.

Реактивное движение.

Уравнение Мещерского.

Реактивное движение - движение тела, при котором от него отделяется (присоединяется) некоторая его часть.

Рассмотрим движение ракеты:

В момент времени t:

m – масса ракеты,

u - скорость ракеты,

В момент времени t + dt:

m + dm – масса ракеты,

u + du - скорость ракеты,

- dm – масса выброшенных газов

(dm < 0),

u – скорость истечения газов относительно ИСО

Используем второй закон Ньютона:

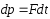
где

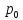- импульс системы в начальный момент времени t,

p - импульс системы в момент времени t + dt.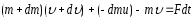

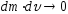
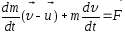
Скорость истечения газов относительно ракеты:

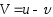
Уравнение Мещерского: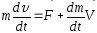

Реактивная сила: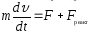

Формула Циолковского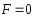

Пусть система замкнута

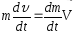
В проекциях на направление движения: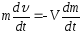

(dm < 0)

Разделим переменные:

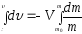
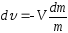
Формула Циолковского: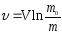

где m₀ – стартовая масса ракеты (вместе с топливом);

m = m₀ – m_топ – полезная масса (масса ракеты без топлива).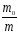

Пусть V » 1 км/с, u = u_I = 7,9 км/с Þ = 2697

15. Закон сохранения механической энергии.

Закон сохранения механической энергии.

Воспользуемся теоремой о кинетической энергии:

При малом перемещении системы изменение этой энергии равно сумме работ, совершаемые при этом внешними и внутренними силами.

Сумму элементарных работ всех сил приложенных к м.т. входящую в рассматриваемую механическую систему, разделим на две части: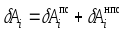

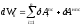
Тогда получим:

Из определения потенциальной энергии следует, что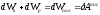

Получаем:

Это уравнение выражает закон изменения механической энергии, где

Если механическая система замкнута и консервативна, то на нее не действуют внешние силы, тогда работа внешних сил равна нулю.

Для таких систем выполняется закон сохранения механической энергии.

Закон сохранения механической энергии:

Полная механическая энергия замкнутой системы тел между которыми действуют только консервативные силы, остается постоянной.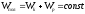

Закон сохранения механической энергии является основным законом механики.

Закон сохранения механической энергии связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны относительно выбора начала отсчета времени.

Если система замкнута, то изменение ее механической энергии обусловлено только действием в ней непотенциальных сил: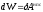

Системы, в которых действуют непотенциальные силы и их механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии, то они называются диссипативными системами.

Диссипация это рассеяние, в данном случае рассеяние энергии.

В природе все системы являются диссипативными.

Закон сохранения и превращения энергии – фундаментальный закон природы, он справедлив как для систем макроскопических тел, так и для систем микротел.

16. Применение законов сохранения к анализу механического удара.

Применение законов сохранения импульса и энергии к расчету абсолютно упругого и неупругого удара.

Удар.

Ударом называется явление изменение скоростей тел на конечные значения за очень короткий промежуток времени, происходящее при их столкновениях.

Силы взаимодействия (внутренние силы) между сталкивающимися телами столь велики, что внешними силами, действующими на них можно пренебречь. Это позволяет систему тел в процессе их соударения приближенно рассматривать как замкнутую систему и применять к ней законы сохранения.

Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара имеет место перераспределение энергии между соударяющимися телами.

В природе нет идеально упругих тел и идеально гладких поверхностей, поэтому относительная скорость тел после удара не достигает своего прежнего значения. Отношение нормальных составляющих относительной скорости тел после удара и до удара называется коэффициентом восстановления e: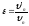

где u_n – скорость тела до удара, – скорость тела после удара.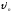

Если для сталкивающихся тел e=0, то такие тела называются абсолютно неупругими, если e=1 – абсолютно упругими.

Прямая, проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения, называется линией удара.

Удар называется прямым, если перед ударом скорости центров масс соударяющихся тел параллельны линии удара, в противном случае удар называется косым.

Удар называется центральным, если центры масс соударяющихся тел лежат на линии удара.

Абсолютно неупругий удар.

Удар называется абсолютно неупругим, если после удара тела объединяются и дальше движутся как одно целое, т.е. с одной и той же скоростью.

При абсолютно неупругом ударе выполняется закон сохранения импульса, а закон сохранения энергии не выполняется.

m₁ и m₂ – массы соударяющихся тел, u₁ и u₂ - скорости этих тел до удара, найдем скорость u этих тел после удара.

Запишем закон сохранения импульса: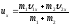

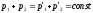
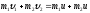
При абсолютно неупругом ударе закон сохранения энергии не выполняется, так как часть механической энергии переходит во внутреннюю (в тепло), т.е. соударяющиеся тела нагреваются.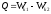

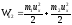
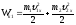
Абсолютно упругий удар.

Абсолютно упругим ударом называется такой удар, при котором механическая энергия соударяющихся тел не преобразуется в другие виды энергии.

При абсолютном упругом ударе выполняются законы сохранения импульса и энергии.

При абсолютно упругом ударе происходит перераспределение механической энергии между соударяющимися телами, и после удара тела движутся с разными скоростями.

В процессе удара систему соударяющихся упругих тел можно считать замкнутой и консервативной.

m₁ и m₂ – массы соударяющихся тел, u₁ и u₂ - скорости этих тел до удара, найдем скорость u₁ и u₂ этих тел после удара.

Запишем закон сохранения энергии:

Запишем закон сохранения импульса:

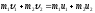
т.к. все скорости направлены вдоль оси ОХ, то из ЗСИ следует, что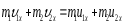

ЗСЭ запишем в следующем виде

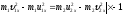
ЗСИ запишем в следующем форме

теперь перепишем ЗСЭ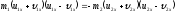

Произведя сокращения получим: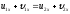

Выразим скорость второго тела после удара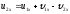

Эту формулу подставим в ЗСИ, получим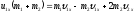

Из этого уравнения находим скорость первого тела после удара: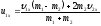

Произведя аналогичные рассуждения получаем формулу для расчёта скорости второго тела после удара:

17. Кинематика вращательного движения.

Кинематика вращательного движения.

Вращательным движением твердого тела называется движение при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Ось вращения может проходить как через вращающееся тело, так и находиться вне этого тела.

Вращающееся тело имеет одну степень свободы вокруг неподвижной оси.

Положение тела в пространстве определяется значением угла поворота вокруг оси вращения.

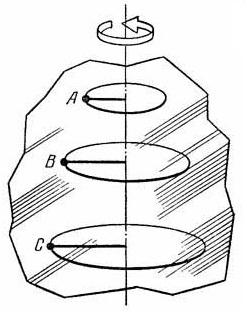
Рассмотрим вращение м.т. по окружности радиуса R.

Пусть в начальный момент времени t₀ м.т. находится в положении M и ее скорость равна u₀.

Спустя промежуток времени dt = t₁ – t₀ м.т. пройдет по окружности путь l и окажется в положении M₁.

Радиус-вектор точки, проведенный из центра O окружности, повернется на угол j.

Угол j называется угловым путем (углом поворота).

Размерность углового пути [j] = 1 рад.

Из геометрии известно, что длина дуги, на которую опирается центральный угол MOM₁, равна: l = jR

Положение тела в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного начального положения этого тела.

Для описания вращательного движения тела неудобно пользоваться понятиями кинематики, как:

1) перемещение;

2) пройденный путь;

3) скорость;

4) ускорение.

В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела .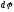

18. Момент инерции материальной точки и момент инерции твердого тела. Теорема Штейнера. Моменты инерции.

Момент инерции.

Рассмотрим твердое тело вращающееся вокруг неподвижной оси OZ.

Основной закон динамики тела, вращающегося вокруг неподвижной оси OZ, имеет вид: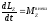

Найдем связь между моментом импульса L_z и угловой скоростью ω.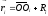

Момент импульса тела относительно начала координат О.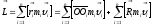

Моменты импульсов точек лежащих на оси вращения равны нулю: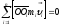

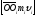
Так как вектор перпендикулярен оси OZ

Вектор направлен оси OZ.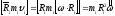

Таким образом,

Величина, равная сумме произведений масс всех материальных точек, образующих механическую систему, на квадраты их расстояний от данной оси вращения, называется моментом инерции системы относительно этой оси: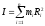

Таким образом, момент импульса тела относительно оси OZ равен: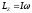

где I – момент инерции тела относительно оси вращения OZ.

Если известен закон распределения массы тела, то момент инерции твердого тела можно определить по формуле:

Моментом инерции м.т. относительно некоторой оси называют скалярную физическую величину, равную произведению массы материальной точки на квадрат расстояния до оси вращения: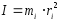

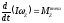
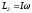
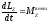
Уравнение с учетом можно написать в виде:

В процессе вращения считается, что I=const, т.е. тело не деформируется: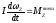

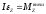
Из уравнения видно, что угловое ускорение обратно пропорционально моменту инерции. Следовательно, момент инерции тела относительно оси является мерой инертности тела в его вращении вокруг этой оси.

Основное уравнение динамики вращательного движения:

В динамике вращательного движения момент инерции играет ту же роль, что и масса в динамике поступательного движения. Момент инерции определяет величину углового ускорения, получаемого телом под действием данного момента силы. Величина момента инерции определяется не только массой тела, но и распределением этой массы относительно оси вращения. Одно и то же тело может иметь различные моменты инерции относительно разных осей, и тела разной массы могут при определенном распределении масс в них иметь одинаковые моменты инерции.

Моменты инерции однородных тел правильной формы.

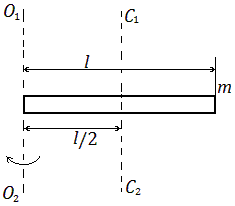
1. Момент инерции тонкого стержня массой m и длинной l относительно оси, проходящей через один из концов стержня перпендикулярно его длине.

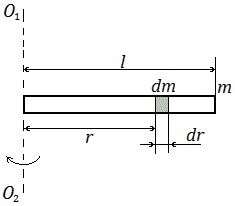
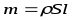
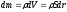
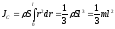
2. Момент инерции тонкого стержня массой m и длинной l относительно оси, проходящей перпендикулярно стержню через его середину.

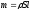
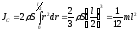
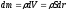
3. Момент инерции однородного кольца (полого цилиндра) массы m и радиуса R относительно его оси.

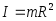
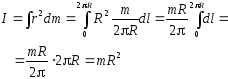
4.Момент инерции однородного сплошного диска (цилиндра) массы m и радиуса R относительно его оси.

Масса диска m = rV = rpR²h, следовательно

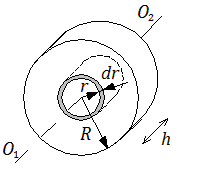
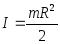
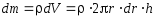
Значения моментов инерции для некоторых тел (тела считаются однородными, m – масса тела)

Тонкое кольцо, материальная точка, полый тонкостенный цилиндр (ось симметрии) :

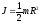
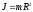
Сплошной цилиндр, диск (ось симметрии):

Диск (ось вращения проходит через диагональ):

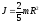
Шар:

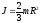
Полая тонкостенная сфера:

Прямой тонкий стержень длиной l, ось перпендикулярна стержню и проходит через его середину:

Прямой тонкий стержень длиной l, ось перпендикулярна стержню и проходит через его конец: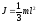

Моменты инерции однородных тел относительно произвольной оси.

Теорема Штейнера:

Момент инерции тела относительно любой оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс и произведение массы тела на квадрат расстояния между осями.

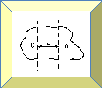
Покажем справедливость теоремы Штейнера на примере со стержнем:

Применение теоремы Штейнера к расчету момента инерции тонкого стержня массой m и длинной l относительно оси, проходящей через один из концов стержня перпендикулярно его длине.

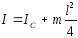
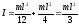
19. Основное уравнение динамики вращательного движения твердого тела. Аналогии между поступательным и вращательным движениями.

Движение твердого тела (плоское движение).

Любое тело можно представить как систему материальных точек. Если расстояние между этими точками остается неизменным, при действии любых сил, то такое тело называют абсолютно твердым.

Поступательным называют движение тела, при котором любая прямая, связанная с телом, перемещается параллельно самой себе.

Вращательным движением твердого тела называется движение при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Плоским движением называется движение точки, если ее траектория плоская кривая, т.е. траектория целиком лежит в одной плоскости.

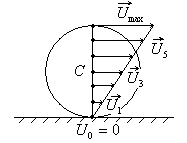
Рассмотрим качение цилиндра по плоскости из положения 1 в положение 2. Это движение можно представить как сумму двух перемещений – поступательного из положения 1 в положение 1’ или 1” и поворота цилиндра вокруг оси О’ или оси О”. Такое разбиение перемещения может быть осуществлено бесчисленным множеством способов, в любом случае поворот цилиндра производится на один и тот же угол j.

Элементарное перемещение точки цилиндра разложим на два – поступательное и вращательное:

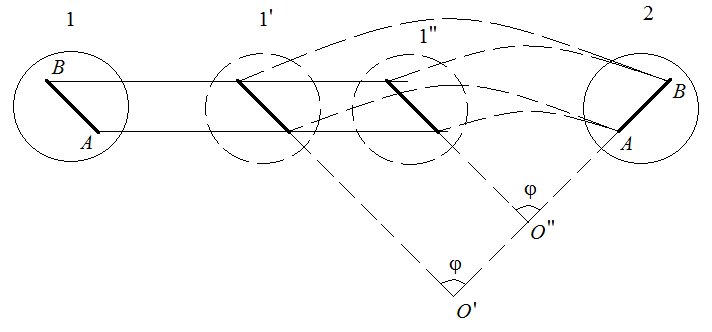
Разделим ds на промежуток времени dt, получим скорость точки: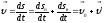

u₀ – одинаковая скорость поступательного движения для всех точек тела;

u' - различная скорость для разных точек тела, обусловленная вращением.

Плоское движение можно представить как сумму двух движений – поступательного со скоростью u₀ и вращательного с угловой скоростью w.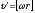

Линейная скорость точки обусловленная вращением тела, равна .

Скорость этой точки при сложном (плоском) движение можно представить в виде:

Движение цилиндра, катящегося без скольжения по плоскости можно представить как поступательное движение со скоростью u₀ и одновременное вращение с угловой скоростью w вокруг оси О, или как поступательное движение со скоростью u=2u₀ и вращение с угловой скоростью w вокруг оси O”, либо как только одно вращение вокруг оси О’ с угловой скоростью w.

Основное уравнение динамики вращательного движения.

Аналогии между поступательным и вращательным движениями.

Поступательное движение	Вращательное движение
Линейное перемещение : Линейная скорость: Линейное ускорение: Масса тела: m Сила: Работа: Мощность: Кинетическая энергия: Импульс тела: Второй закон Ньютона:	Угловое перемещение: Угловая скорость: Угловое ускорение: Момент инерции: I Момент силы: Работа: Мощность: Кинетическая энергия: Момент импульса: ОУДВД:

20. Относительность движения в классической физике.

Принцип относительности Галилея:

Все законы механики одинаковы во всех ИСО.

Преобразования Галилея позволяют сделать переход из одной ИСО в другую. В его основе лежат две аксиомы:

аксиома 1 – ход времени одинаков во всех системах отсчета.

аксиома 2 – расстояния между двумя точками, а также размеры тела в любой системе отсчета (СО) не зависят от скорости ее движения.

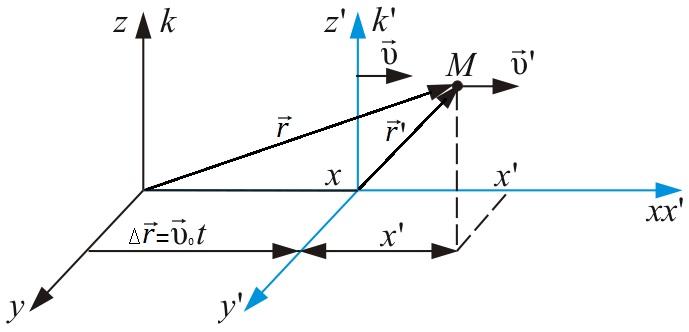
Рассмотрим две ИСО:

К – лабораторная (неподвижная) СО Oxyz

К¢ - движущаяся СО O¢x¢y¢z¢

u₀ - скорость движения системы K¢ относительно системы K.

В начальный момент времени оси координат обеих СО совпадают. Пусть внутри системы K¢ находится некоторое тело M.

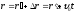
Спроектируем на координатные оси: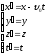

1. Или (2)

Системы уравнений (1) и (2) называются преобразованиями Галилея.

Используя уравнения (1) и (2), можно перейти от описания движения тела в одной системе отсчета к другой системе отсчета.

Из преобразований Галилея вытекает теорема (закон) сложения скоростей.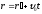

Продифференцируем по времени:

(u₀ = const)

Теорема о сложении скоростей в классической механике: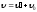

u - скорость движения точки в неподвижной ИСО К; u¢ - скорость движения точки в движущейся ИСО K¢; u₀ - скорость движения системы K¢ относительно системы K.

В теоретической механике эту теорему записывают в виде:

Продифференцируем полученное выражение по времени еще раз:

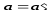
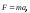
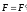
Инвариантные величины:

Величины, не изменяющиеся при переходе от одной системы отсчета к другой, т. е. не зависящие от преобразований координат, называются инвариантными величинами или инвариантами преобразований.

1. Ускорение;

2. Силы;

3. Масса;

4. Длина тела и т. д.

Принцип относительности Галилея: законы механики одинаковы во всех инерциальных системах отсчета.

Это значит, что в разных ИСО все механические процессы при одних и тех же условиях протекают одинаково.

Инвариантными по отношению к преобразованиям Галилея, при переходе от одной ИСО к другой, оказываются также уравнения, вид которых не изменяется при таком переходе. Величины, входящие в эти уравнения, могут при переходе от одной СО к другой изменяться, однако формулы, выражающие связь между этими величинами, остаются неизменными.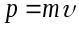

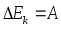
Принцип относительности Галилея: уравнения механики инвариантны по отношению к преобразованиям Галилея.

21.Постулаты СТО. Преобразования Лоренца.

Постулаты СТО.

1-ый постулат СТО (принцип относительности Эйнштейна) является обобщением классического принципа относительности с механических на любые физические явления.

Первая формулировка. Никакими физическими опытами (механическими, электрическими, оптическими) проведенными в ИСО, нельзя доказать покоится эта система или движется равномерно и прямолинейно относительно другой ИСО.

Вторая формулировка. Все процессы в природе (механические, электрические, оптические) во всех ИСО протекают одинаково.

Эйнштейн показал, что преобразования Галилея должны быть заменены более общими преобразованиями Лоренца.

Третья формулировка. уравнения выражающие законы природы, инвариантны по отношению к преобразованиям Лоренца.

2-ой постулат СТО (принцип инвариантности скорости света). Скорость света в вакууме не зависит от скоростей движения источника и приемника света, и является максимально возможной скоростью движения в природе.

c = 3,00·10⁸ м/с

Из второго постулата следует, что скорость света в вакууме является величиной инвариантной, т. е. она одинакова для всех направлений и во всех ИСО.

Скорость света является одной из важных физических постоянных и она в вакууме является предельной.

Опыты показали, что скорость любых тел и частиц, а также скорость распространения любых сигналов и взаимодействий не может превосходить скорости света.

Механика, описывающая движения с околосветовыми скоростями, называется релятивистской механикой.

В СТО пространство и время взаимосвязаны, образуя единое четырехмерное пространство-время.

Точечное» событие характеризуется четырьмя величинами – координатами x, y и z, указывающими, где оно произошло, и временем t – когда оно произошло.

Значения этих четырех величин зависят от СО, в которой «наблюдаем» это событие.

В четырехмерном пространстве (пространство–время) возьмем прямоугольную систему координат с осями x, y, z и ct. Тогда событие можно изобразить точкой, которую называют мировой точкой.

С течением времени мировая точка изменяет свое положение в четырехмерном пространстве, описывая траекторию, которая называется мировой линией.

Если частица неподвижна в обычном пространстве, ее мировая точка перемещается параллельно оси ct.

При переходе к другой ИСО значения координат x, y, z, а также времени t изменяются и становятся равными x¢, y¢, z¢ и t¢.

Пространство:

Классическая механика	Релятивистская механика
Евклидовое – трехмерное М (x, y, z) Время однородно, пространство однородно и изотропно. Время и пространство отделены друг от друга	Минковского – четырехмерное М (x, y, z, ct) Время однородно, пространство однородно и изотропно. Время и пространство отделены друг от друга

Преобразования Лоренца.

В релятивистской механике преобразования координат Галилея заменяются на преобразования координат Лоренца.

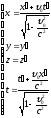
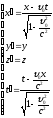
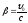
Иногда для упрощения записи вводят релятивистский множитель:

Если u₀ << c (b << 1), то преобразования Лоренца переходят в преобразования Галилея.

Из преобразований Лоренца можно получить ряд следствий.

22. Следствия из преобразования Лоренца.

Относительность одновременности событий.

Пусть в системе K в двух разных точках с координатами x₁ и x₂ (x₁ ¹ x₂) в один и тот же момент времени (t₁ = t₂) происходят два события.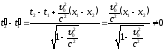

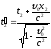
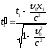
События, одновременные в системе К, в системе К¢ оказываются неодновременными, т. е. одновременность событий – относительна.

Вывод: Время – неинвариантная величина.

Релятивистское изменение длины.

Пусть в системе K¢ покоится стержень длиной l₀ = x₂¢ - x₁¢ (собственная длина тела).

Длина стержня в системе K равна l = x₂ - x₁, где x₁ и x₂ – координаты концов стержня в системе K, измеренные в один и тот же момент времени (t₁ = t₂).

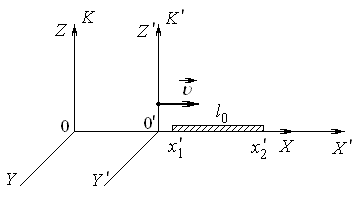
Используем прямые преобразования координат: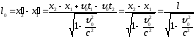

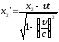
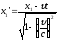
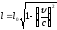
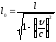
Это и есть релятивистское изменение длины:

Его также называют лоренцевым сокращением длины.

Размеры тела относительно неподвижной СО сокращаются только в направлении движения относительно неподвижной системы отсчета.

а) тела неподвижные;

б) тела движутся со скоростью u .

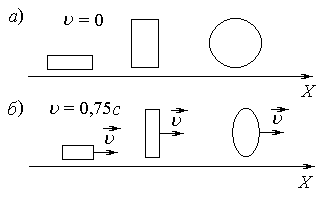
Следствия:

1. , то и - классическая физика.