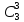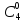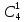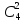1
.docx1)Теоремы о сложении и умножении
Теорема о сложении:
Пусть объект
 может быть выбран
может быть выбран
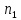 способами,
способами,
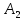 -
-
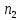 и т.д.
и т.д.
 -
-
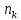 ,
тогда выбор одного из объектов
,
тогда выбор одного из объектов
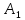 ,
,
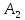 ,
,
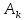 может быть осуществлено
может быть осуществлено
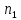 +
+
 +
+
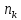 (=
(=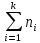 )
способами.
)
способами.
Теорема об умножении:
Пусть элемент
 может быть выбран
может быть выбран
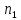 способами,
способами,
 -
-
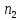 и т.д.
и т.д.
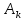 -
-
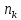 ,
тогда выбор
,
тогда выбор
 ,
,
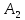 ,
,
 (упорядоченный) может быть осуществлен
(упорядоченный) может быть осуществлен
 *
*
 *
*

Доказательство:
K=2
1,2…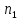 - способы выбора элемента
- способы выбора элемента
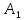
Каждому из
них соответствует
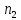 способов выбрать элемент
способов выбрать элемент

(1,Х) -
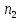 пар
пар
(2,Х) -
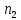 пар
пар
…
(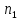 ,
Х) -
,
Х) -
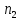 пар
пар
Общее число
={
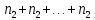 }
=
}
=
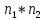
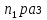
К=3
1,2…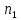 - способы выбора
- способы выбора
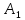
Каждому из
них соответствует
 *
*
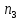 способов выбора двух других элементов
способов выбора двух других элементов
(1, Х, У) -
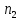 *
*
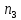
(2, Х, У) -
 *
*

…
(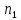 ,
Х, У) -
,
Х, У) -
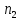 *
*
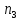
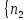 *
*
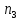 +
+
 *
*
 +…+
+…+
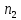 *
*
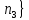 =
=
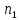 *
*

2) Формула включений – исключений.
Теорема:
пусть имеется K свойств
(1, 2, …, К), несколько объектов, каждый из
которых может удовлетворять или не
удовлетворять свойствам.
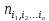 – количество объектов, удовлетворяющие
всем свойствам
– количество объектов, удовлетворяющие
всем свойствам
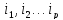 .
.
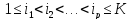 ,
тогда количество объектов (Х),
удовлетворяющих хотя бы одному из этих
свойств, может быть посчитано:
,
тогда количество объектов (Х),
удовлетворяющих хотя бы одному из этих
свойств, может быть посчитано:
Х = (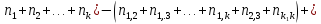
K – нечетное => последнее слагаемое с «+»
Следствие:
Если К=2, то
Х=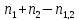
Если К = 3, то
Х=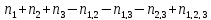
Доказательство:
Теорема о сложении:
К=2
Х=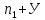 ,
где
,
где
У – число
элементов, удовлетворяющих
 и
не удовлетворяющих
и
не удовлетворяющих
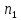 ,
т.е. У+
,
т.е. У+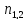 =
=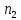 =>
=>
Х= +(
+(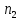 -
-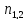 )=
)= +
+ -
-
Теорема об умножении:
К=3
Х=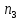 +(
+(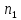 +
+ -
-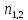 )-(
)-( +
+ +
+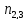 )-n…=
)-n…=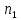 +
+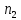 +
+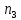 -
-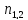 -(
-( +
+ -
-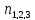 )
)
Пусть У –
число элементов, удовлетворяющих
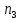 и хотя бы одному
и хотя бы одному
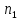 или
или
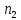 ,
,
Z – количество
элементов, которые удовлетворяют хотя
бы одному
 или
или
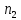
Z= +
+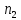 -
-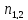
X=Z+ -y
-y
Y=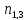 +
+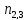 -
-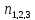
X= +
+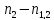 +
+ -
-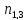 -
-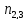 +
+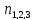
X= +
+ +-
+- -
-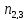 )+
)+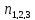
3)Размещения с повторениями. Их число
Размещение – выборка, порядок в которой важен
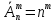
Пример: найти все 12 значные числа, все цифры которых нечетны
n=5, т.к. цифры 1,3,5,7,9; m=12 (5*5*5*…*5) 12 раз
при m=0, выборка принимает значение 1, т.е. ничего не выбрать
4)Размещения без повторений
Размещение – выборка, порядок в которой важен
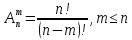
m>n, выборка =0
Пример: Имеется группа студентов из 11 человек, необходимо выбрать старосту, заместителя старосты, профорга, культорга, казначея
Решение:
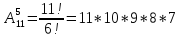
Доказательство:
Пусть m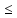 n
n
Первый может выбрать n способами
Второй – n-1 способами
Третий – n-2 способами
Последний n-(m-1) способами
Всего способов:
n*(n-1)(n-2)…(n(m-1))=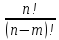
5) Перестановки
Перестановкой называется размещение без повторений, если количество выбираемых элементов равно общему количеству имеющихся
P_n=A_n^n=n!/(n-n)!=n!/0!=n!
Пример: сколько различных слов можно получить, если перемешать все буквы слова ВЕРБЛЮД (7!)
6)Сочетания без повторений
Сочетание – выборка без учета порядка
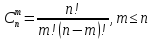
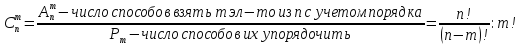
m>n выборка = 0
Пример: Необходимо провести отбор 10 игроков из 15 для формирования команды. Сколько различных команд можно создать
=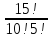
7) Свойства числа сочетаний.
1).
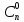 =1
Доказательство: 1 способ: Кол-во способов
выбрать 0 элементов из набора n
равно 1 способу.
=1
Доказательство: 1 способ: Кол-во способов
выбрать 0 элементов из набора n
равно 1 способу.
2 способ: =
=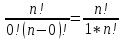 =1
=1
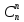 =1
Доказательство: 1 способ: Кол-во способов
выбрать n элементов из n
имеющихся равно 1 способу.
=1
Доказательство: 1 способ: Кол-во способов
выбрать n элементов из n
имеющихся равно 1 способу.
2 способ:
 =
=
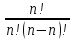 =
1/0!=1
=
1/0!=1
2).
 =n
Доказательство: 1 способ: Кол-во способов
выбрать 1 элемент из n имеющихся равно
n способам.
=n
Доказательство: 1 способ: Кол-во способов
выбрать 1 элемент из n имеющихся равно
n способам.
2 способ:
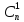 =
=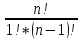 =n
=n
3).
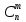 =
=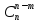
Доказательство:
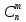 =
= =
=
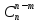 =
=
4).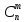 =
= +
+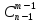 , при n>1, m<n
, при n>1, m<n
Доказательство:
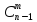 +
+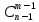 =
= +
+
 =
=
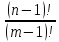 *
*
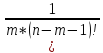 +
+
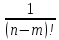 )
=
)
=
 *
*
 +
+
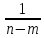 )=
)=
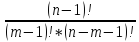 *
*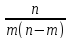 =
=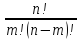 =
=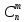
8) Бином Ньютона и треугольник Паскаля
Треугольник Паскаля:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
Бином Ньютона:

Доказательство:
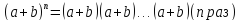
По правилу умножения при раскрытии скобок берется слагаемое, эти слагаемые перемножаются, все возможные произведения складываются
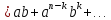
Приведем
подобные слагаемые, количество слагаемых
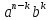 =
количество способов выбрать к скобок
из n (из выбранных выбираем
b) =
=
количество способов выбрать к скобок
из n (из выбранных выбираем
b) =
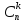
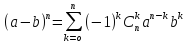
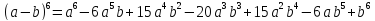
9)Сочетания с повторениями. Примеры.
Сmn=Cmm+n-1=Cn-1m+n-1
Доказательство
Сmn
11..101…101…101…1-сочетание
с повторениями



K1 K2 K3 Km
Ki –количество i элементов в сочетании 0<=k<=m , где ki –целое

Сmn –количество последовательностей из 0 и 1 причем :
0=n-1
1=m
Всего (m+n-1) –место на котором (n-1)=1, а остальное =0
Сm-1m+n-1=Cmm+n-1
Сmn=Cn-1m+n-1=mm+n-1
10)Понятие высказывания. Основные логические операции.
Высказывание – любое утверждение, про которое можно сказать истинно оно или ложно.
Высказывание обозначается заглавной буквой латинского алфавита, возможно с индексом.
Основные логические операции:
Отрицание:
Под отрицание А подразумевается высказывание, которое истинно только тогда, когда высказывание А – ложно
Синонимы: «неверно, что…»
Обозначение:

 - закон двойного отрицания
- закон двойного отрицания
Дизъюнкция или логическое сложение:
Дизъюнкцией высказывания А и В называют высказывание, которое истинно, если А или В истинно.
Синонимы: «Или А или В»
Обозначение:
Конъюнкция или логическое умножение
Конъюнкцией высказывания А и В называют высказывание, которое истинно только тогда, когда истинны оба высказывания
Синонимы: « И А и В»
Обозначение:

Импликация или логическое следование
Импликацией высказывания А и В называют такое высказывание, которое истинно только тогда, когда либо ложна посылка, либо истинно заключение
Синонимы: «Если…, то…», «…влечет…», «…следует из…»
Обозначение:

Эквивалентность
Эквивалентным высказывание является высказывание, которое истинно только тогда, когда А и В принимают одинаковы значения истинности
Синонимы: «А только тогда, когда В», «если и только если», «А влечет В и наоборот», «А и В равносильны»
Обозначение:
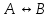
О – тождественно ложное высказывание (всегда ложно)
1 – всегда истинно
11) Логические функции. Таблицы истинности. Эквивалентность формул логики высказываний.
Функции логики высказывания:
Пусть
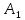 ,
,
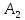 …
…
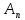 -
логические переменные (либо истинно,
либо ложно), тогда под функцией (
-
логические переменные (либо истинно,
либо ложно), тогда под функцией (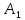 ,
,
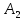 …
…
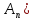 - правило, которой каждой последовательность
значений переменной.
- правило, которой каждой последовательность
значений переменной.
Функция логики высказывания строго задается таблицей истинности
Строк в таблице истинности 2^n
Функции называют одинаковыми, если их таблицы истинности совпадают.
Всякое формуле логики высказывания соответствует однозначно определенная функция логики высказываний. При этом элементарным высказыванием становится переменная данной функции.
Бывают
ситуации, когда разные формулы логики
высказываний задают одну функцию (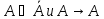 ).
Формулы логики высказываний, задающие
одну и ту же функцию называют эквивалентами.
).
Формулы логики высказываний, задающие
одну и ту же функцию называют эквивалентами.
Если F
 и, то F называется
тавтологией, если F
и, то F называется
тавтологией, если F
 л, то F называется тожественно
ложной функцией.
л, то F называется тожественно
ложной функцией.
Функции зависят от одних и тех же переменных.
Эквивалентность
формул логики высказываний.

Коммуникативность
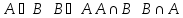
Ассоциативность
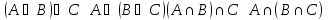
Дистрибутивность
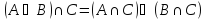

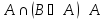

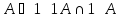


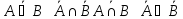

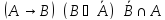 )
)

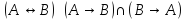
12) Основные законы алгебры высказываний
1) Коммутативность
А В = В А
А В = В А
2) Ассоциативность
(А В) С = A (B C)
(А В) С = A (B C)
3) Дистрибутивность
А (В С) = (A B) (A C)
А (В С) = (A B) (A C)
4) Поглощение
A (B A) = A
A (B A) = A
5) A A = A
A A = A
6) A И = И
A И = А
7) A Л = А
A Л = Л
8) Двойное отрицание
А = А
9) Законы де Моргана
А B = A B
А B = A B
10) И = Л
Л = И
11) А В = В А
А В = В А
12) Доказательство от противного
А В = В А
13) А В = (А В) (В А)
13) Совершенные формы
Дизьюнктивной нормальной формулой (ДНФ) называется дизьюнкция элементарных коньюнктов, при этом коньюнкты не должны повторяться.
Совершенной дизьюнктивной нормальной формулой (СДНФ) называется такая ДНФ в любой коньюнкт которой входят все переменные формулы.
Коньюктивной нормальной формулой (КНФ) называется коньюнкция элементарных дизьюнктов, при этом дизьюнкты не должны повторяться.
Совершенной коньюнктивной нормальной формулой (СКНФ) называется такая КНФ в любой дизьюнкт которой входят все переменные формулы.
Теорема 1: всякая формула отличная от тождественно ложной имеет СДНФ и эта форма единственная с точностью до пеестановки элементарных коньюнктов и порядка переменных в этих коньюнктах.
Теорема 2: всякая формула отличная от тафтологии имеет СКНФ и эта форма единственная с точностью до пеестановки элементарных дизьюнктов и порядка переменных в этих дизьюнктах.
Доказательство 1:
1)Пусть есть функция f (A1 … Аn) не тождественно ложная
Рассмотрим ее таблицу истинности: каждой строке поставим в соответствии элементарный коньюнкт, где Хi = Аi , если Аi = И
Хi = Аi , если Аi = Л
Дизьюнкция берется по все строчкам, в которых f=И.
F - СДНФ
Возьмем любую строку таблицы
1. Если f=И, тогда все коньюнкты в этой строке истинны, следовательно, F=И
2. Если f=Л, тогда все коньюнкты в этой строке ложны, следовательно, F=Л
2)Всякому элементарному коньюнкту , который входит в СДНФ соответствует одна строка таблицы истинности, всякий элементарный коньюнкт истинен только в той строке, которой он соответствует, следовательно, каждый из СДНФ задает именно единственную функцию.
Доказательство 2:
Аналогично доказательству 1.
14) Зависимость связок.
Определение: система логических операций называется полной, если всякая логическая функция может быть представлена в виде конечной последовательности операций из этой системы.
 – полная система, т.к. всякая логическая
функция имеет дизъюнктивную норм фору,
либо конъюнктивную
– полная система, т.к. всякая логическая
функция имеет дизъюнктивную норм фору,
либо конъюнктивную
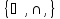 - неполная, т.к. нельзя записать
- неполная, т.к. нельзя записать
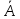
Если система
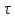 полна, то система
полна, то система
 тоже
полна, если
тоже
полна, если
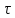 неполна, то и любая ее подсистема также
неполна.
неполна, то и любая ее подсистема также
неполна.
Пример полных систем:
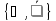
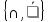
Пример неполных систем:
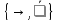
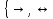 }
}
{ }
}
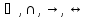
15)Связь теории высказываний и теории множеств
Теорема. Пусть одна некоторая формула логики высказываний, которая не содержит импликацию и эквивалентность. Каждой из переменных поставим в соответствие какое-либо множество.
Заменим Ai на Bi; ∨ на⋃; ∧ на ⋂
Получим Т(В1,…,Вn)
Пусть Ai: х⊂Bi, тогда F-истинно⟷x⊂T
Пример
F=A1∨неA2
![]()
T=B1⋃B2
Доказательство от противного
Пусть не так.
Пусть F-формула,для которой
заключение не выполняется и которая
содержит наименьшее число операций,
заметим, что F-неэлементарная
формула (если F=Ai,
то T=Bi и F
удовлетворяет условию теоремы).Тогда
или F=G или
F=G1∨G2
или F= G1∧G2И
при том в G операций меньше,
чем в F=> для Gi
выполнено условие теоремы:
16) Логические следствия и доказательства. Примеры.
Говорят, что высказывание В является логическим следствием высказываний (А1,A2,…,An),если (A1ᴖA2,…,ᴖAn)→B=И
Пример:
Т1 : “диагонали ABCD делятся таким образом пополам, 0= АСᴖBD”
T2: “ ABCD”-параллелограмм
Т2↔Т1 F=((Т2↔Т1)ᴖТ1)→Т2~И
Т1/Т2
|
Т1 |
Т2 |
Т2→Т2 |
(Т2→Т1)ᴖТ1 |
F |
|
И И Л Л |
И Л И Л |
И И Л И |
И И Л Л |
И Л И И |
Пример
Т1: число нечетно
Т2: число простое
Т1→Т2((Т1→Т2)ᴖТ1) →Т2~И
Т1/Т2
Ā1 ⋃ Ā ⋃ … ⋃ Ān ⋃ В
(А1ᴖА2 ᴖЛ…Л
Аn)→В~(А1ᴖА2 ᴖ…ᴖАn)
⋃ В~Ā1 ⋃
Ā2 ⋃ … ⋃
Ān ⋃
B
17) Понятие предиката. Определение, примеры. Логические операции над предикатами.
Определение
X1,X2,…,Xn- множество
X1*X2*,…,*Xn
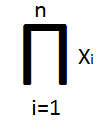 – декартово произведение
– декартово произведение
Определение
n-местный предикат р(X1,X2,…,Xm)-это логическая функция которая действует
X1*X2*X3*…*Xn →{И,Л}
Определение
А - называется
область истинности предиката р(X1,…,Xn)
≡(X1,X2,…,Xn)
∈A<=>p(X1,X2,…,Xn)=
И![]()
Предикаты называются равными если область их истинности совпадает.
Одноместный предикат-это свойство.
Если предикат двухместный он показывает бинарные отношения.
n-местный предикат называется n-арным отношением.
Для предикатов определены все операции. В дальнейшем мы будем полагать, что все предикаты лежат в одном множестве.
Р(X) x>3
P(T) T-четырехугольник это квадрат
Р1 (R,C)
R-(числовая прямая)=(-∞;∞)
C={T; T-четырехугольник}
Мы считаем, что все предикаты лежат в одном множестве, тогда для них определены все операции-Р1,Р2-предикаты определенные на X1*X2*…*Xn
1)P1 – множество истинности которого дополнение до множества истинности предиката P1
2)неP1 ⋃ P2-предикат множество истинности которого совпадает с объединением множества истинности предиката
3) P1 ⋂ P2-предикат множество истинности которого является совпадение с пересечением множеств истинности предиката P1 P2
4) P1 →P2 ∽P1 ⋃неP2 предикат множеством истинности которого
явл. совпадение объединений множеств истинности предикатов P1 и Р2
5)Р1↔Р2∽(Р1⋂P2)⋃(P1⋂P2)
P≡И множество истинности = x1*x2*…*xn
P≡Л множество истинности пусто
18) Свободные и связанные переменные. Кванторы всеобщности и существования, х взаимосвязь.
Квантор всеобщности. Символ x называется квантором всеобщности.(любой, всякий, каждый) Выражение xP(x) читается: “Для всех x имеет место P(x)”. Возможно отрицание :xP(x): “Не для всех x имеет место P(x)”.