
11.2. Дифференциальные уравнения, допускающие понижение порядка
Дифференциальным
уравнением
![]() -го
порядка
называется уравнение вида
-го
порядка
называется уравнение вида
![]() .
(11.12)
.
(11.12)
Интегрирование
дифференциальных уравнений
![]() -го
порядка (в конечном виде) удается
произвести только для некоторых частных
случаев.
-го
порядка (в конечном виде) удается
произвести только для некоторых частных
случаев.
Решение уравнения
![]() находится
находится
![]() -кратным
интегрированием, а именно:
-кратным
интегрированием, а именно:
![]() ,
,
![]() ,
,
![]() ,
,
……………………………………………………
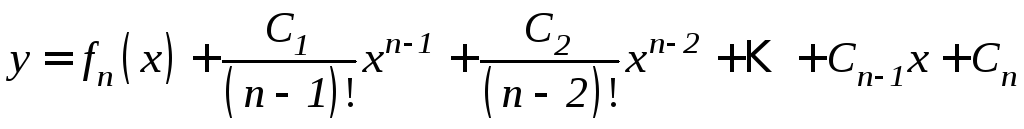 ,
,
где
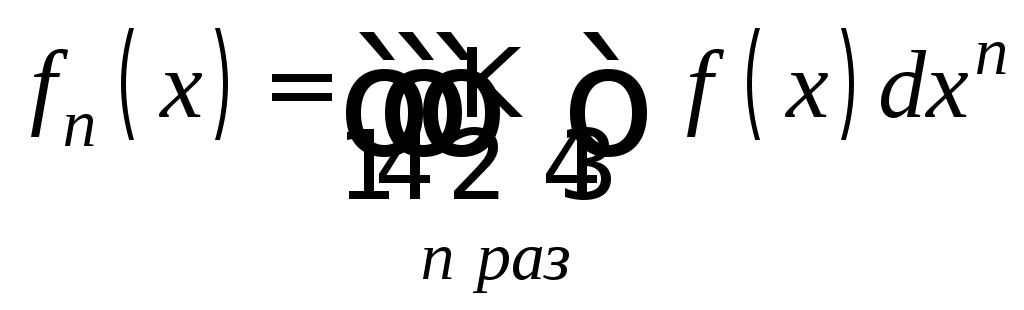 .
.
Так как
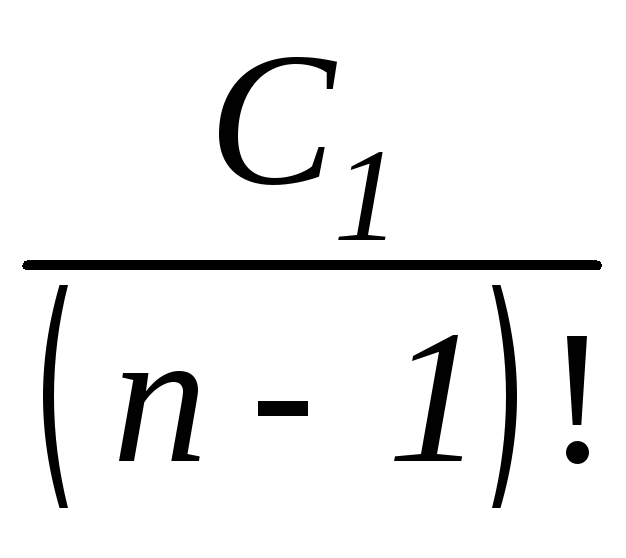 ,
,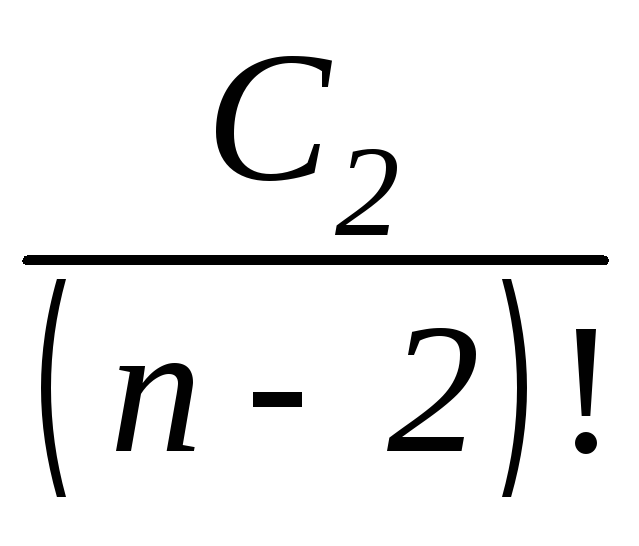 ,
… являются постоянными величинами,
то общее решение может быть записано
так:
,
… являются постоянными величинами,
то общее решение может быть записано
так:
![]() .
.
Пример 15. Решить дифференциальное уравнение
![]() .
.
Решение. Последовательно интегрируя четыре раза данное уравнение, получим
![]() ,
,
![]() ,
,
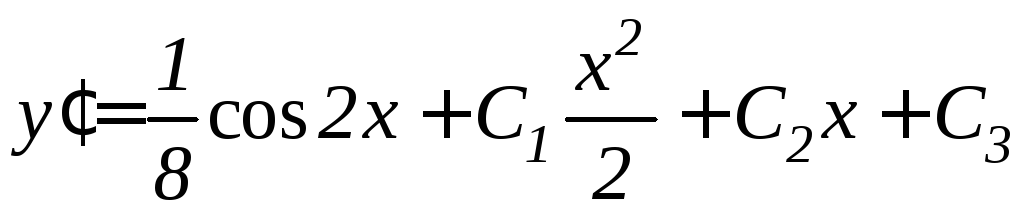 ,
,
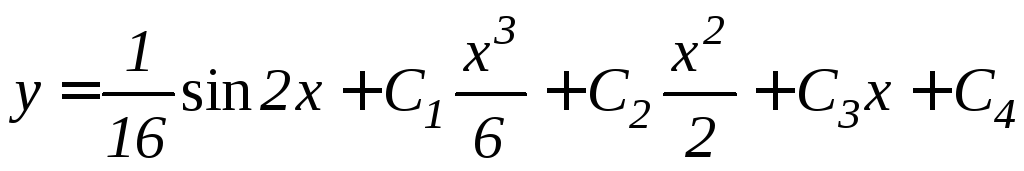 .
.
Порядок уравнения вида
![]()
можно понизить,
взяв за новую неизвестную функцию низшую
из производных данного уравнения, т.е.
полагая
![]() .
Тогда получим уравнение
.
Тогда получим уравнение
![]() .
.
Таким образом,
порядок уравнения понижается на
![]() единиц.
единиц.
Пример 16. Найти общее решение дифференциального уравнения
![]() .
.
Решение.
Поскольку
уравнение не содержит
![]() ,
то полагая
,
то полагая![]() ,
имеем
,
имеем![]() .
Получаем дифференциальное уравнение
.
Получаем дифференциальное уравнение
![]() .
.
Разделив его на
![]() ,
получим линейное неоднородное уравнение
,
получим линейное неоднородное уравнение
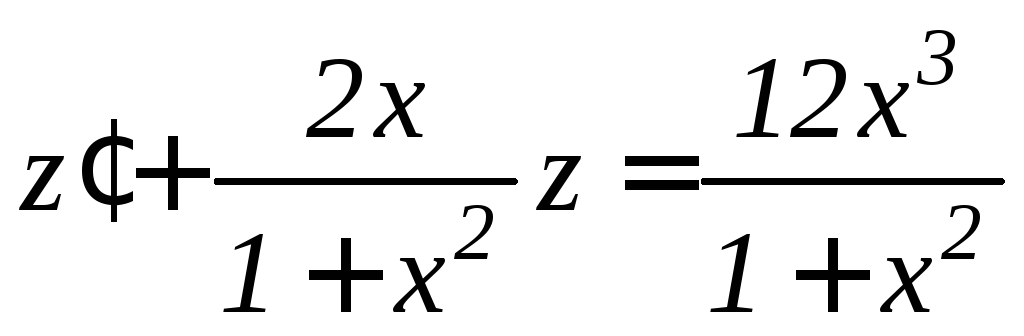 .
.
Решая однородное уравнение, получаем
![]() ,
,
![]() ,
,![]() .
.
Решаем неоднородное уравнение, например, методом вариации постоянных:
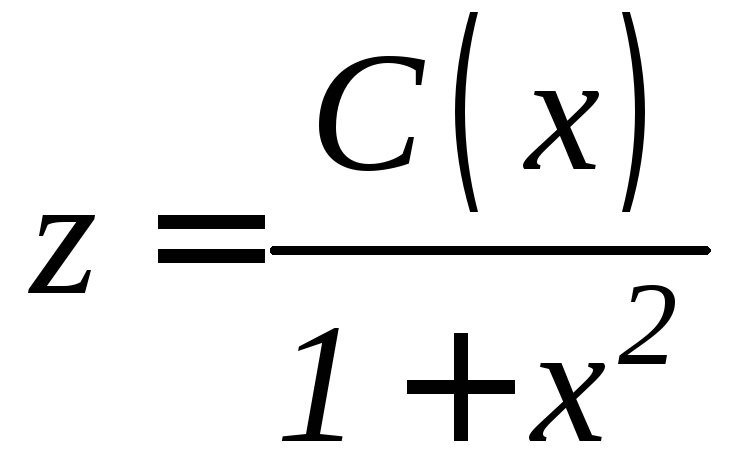 ,
,
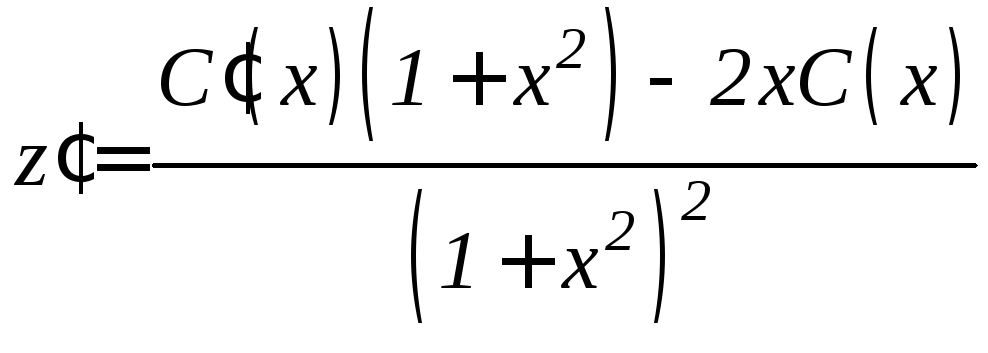 ,
,![]() ,
,![]() .
.
Таким образом, решением является
 .
.
Т.к.
![]() ,
имеем
,
имеем
 .
.
Интегрируя, получим общее решение
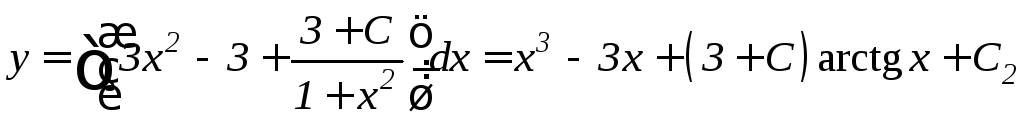
или
![]() .
.
Уравнение вида
![]()
допускает понижение
порядка на единицу, если положить
![]() ,
а за новый аргумент принять сам
,
а за новый аргумент принять сам![]() .
В этом случае
.
В этом случае![]() ,
,![]() ,
… выразятся через
,
… выразятся через![]() и производные от
и производные от![]() по
по![]() по формулам
по формулам
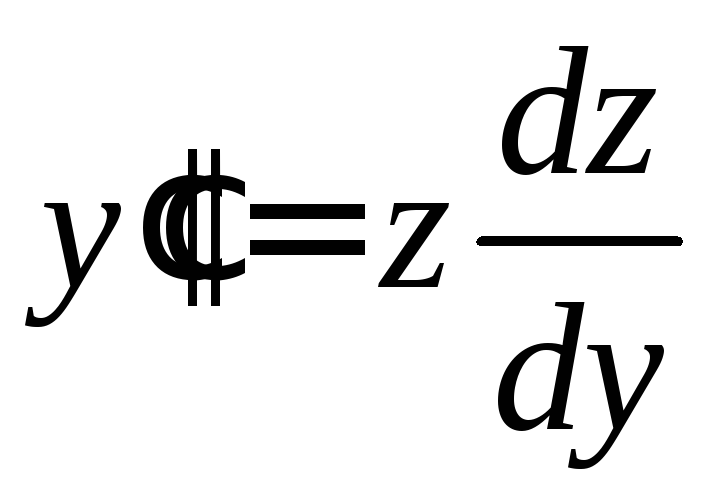 ,
,
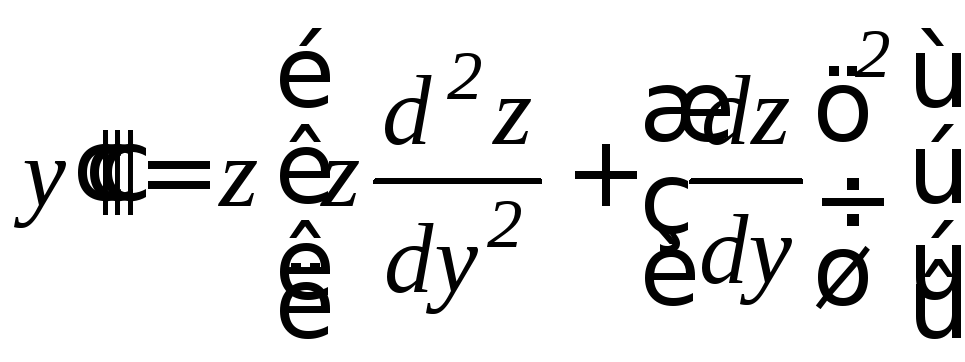 ,
…
,
…
(они выводятся по правилу дифференцирования сложной функции), причем порядок уравнения понизится на единицу.
Пример 17. Найти решение уравнения
![]() .
.
Решение.
Положив
![]() и приняв
и приняв![]() за новую независимую переменную, получим
за новую независимую переменную, получим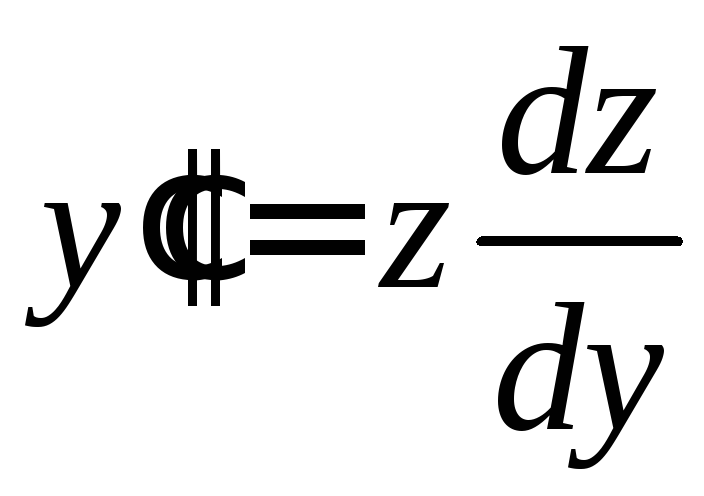 .
Тогда данное уравнение можно записать
в виде
.
Тогда данное уравнение можно записать
в виде
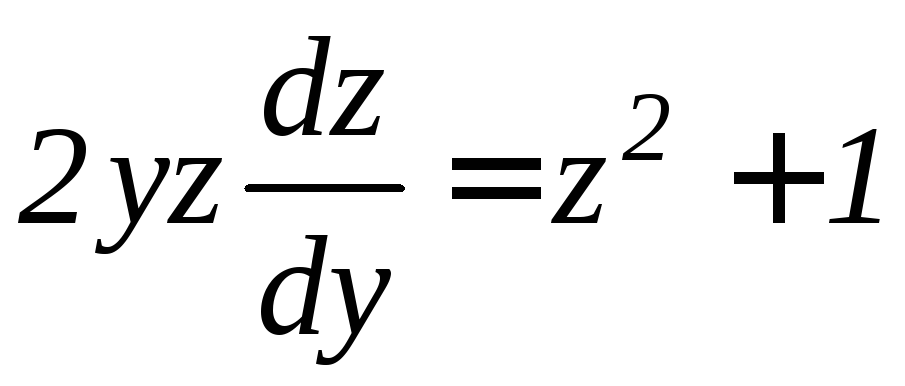 .
.
Полученное уравнение – с разделяющимися переменными:
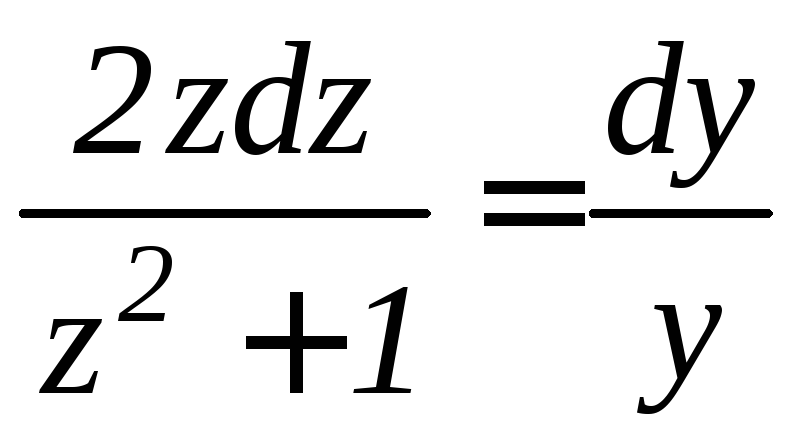 или
или
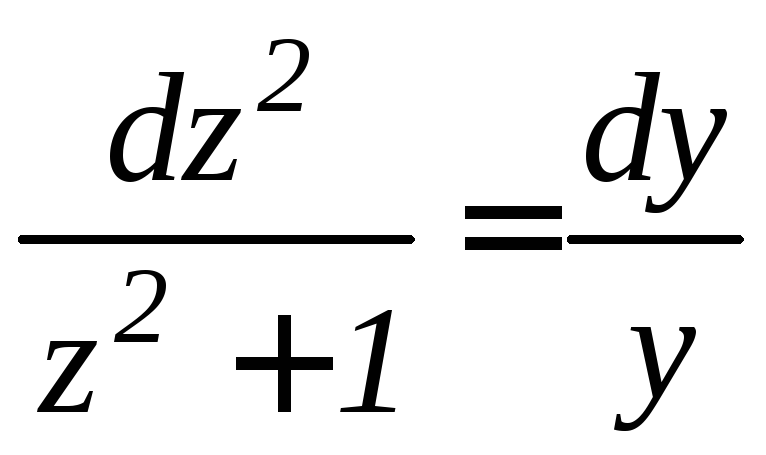 .
.
Интегрируя, получаем
![]() ,
,
![]() .
.
Т.к.
![]() ,
то приходим к следующему уравнению
относительно
,
то приходим к следующему уравнению
относительно![]()
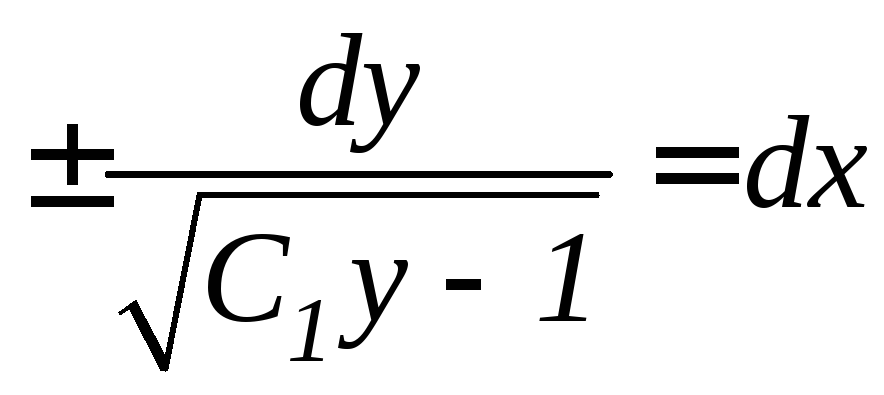 .
.
Находя интеграл, получаем
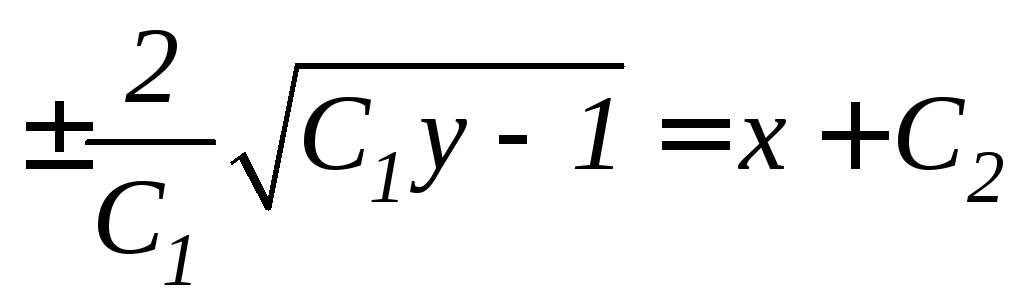 ,
,
![]()
или окончательно
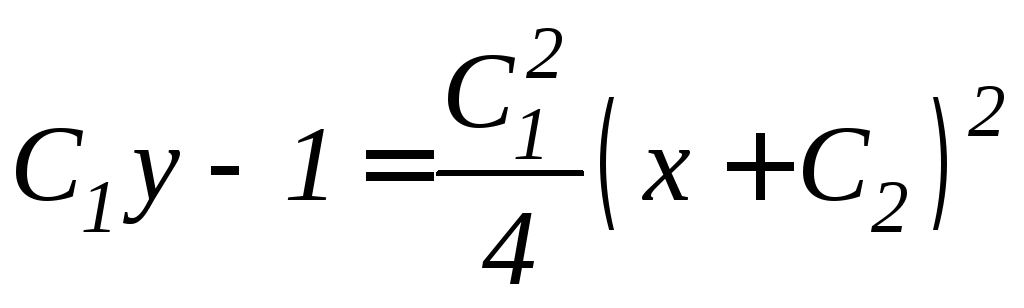 .
.
11.3. Линейные уравнения с постоянными коэффициентами
Дифференциальное уравнение
![]() ,
(11.13)
,
(11.13)
где коэффициенты
![]() ,
,![]() ,
…,
,
…,![]() ,
,![]() - некоторые действительные числа,
называетсялинейным
однородным уравнением n
-го порядка с постоянными коэффициентами.
- некоторые действительные числа,
называетсялинейным
однородным уравнением n
-го порядка с постоянными коэффициентами.
Общее решение уравнения (11.13) определяется формулой
![]() ,
,
где
![]() ,
,![]() ,
…,
,
…,![]() - его линейно независимые частные
решения.
- его линейно независимые частные
решения.
Для нахождения частных решений уравнения (11.13) составляют характеристическое уравнение
![]() ,
(11.14)
,
(11.14)
которое получается
из уравнения (11.13) заменой производных
искомой функции соответствующими
степенями
![]() ,
сама функция заменяется единицей.
Уравнение (11.14) является уравнением
,
сама функция заменяется единицей.
Уравнение (11.14) является уравнением![]() -й
степени и имеет
-й
степени и имеет![]() корней (действительных или комплексных,
среди которых могут быть и равные).
корней (действительных или комплексных,
среди которых могут быть и равные).
Общее решение дифференциального уравнения (11.13) строится в зависимости от характера корней уравнения (11.14):
каждому действительному простому корню
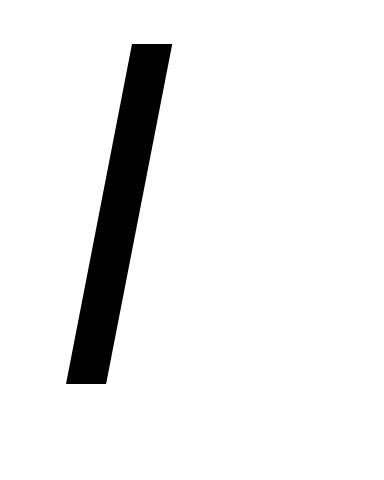 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида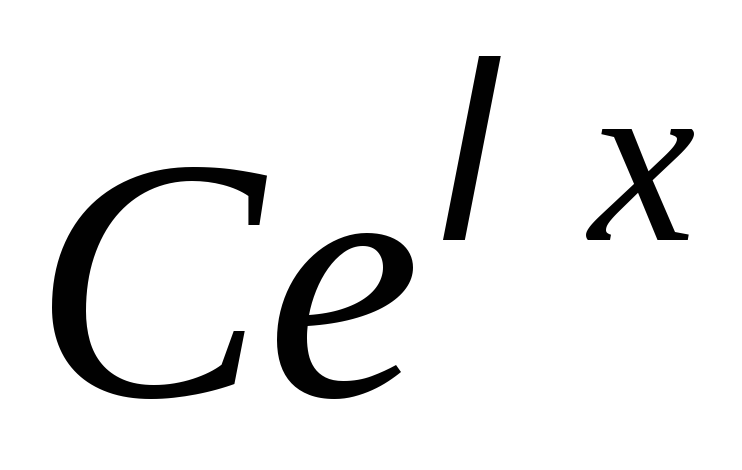 ;
;каждому действительному корню кратности
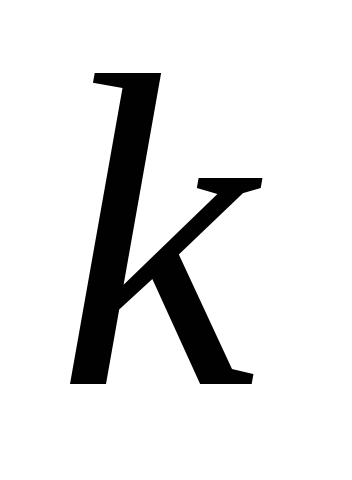 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида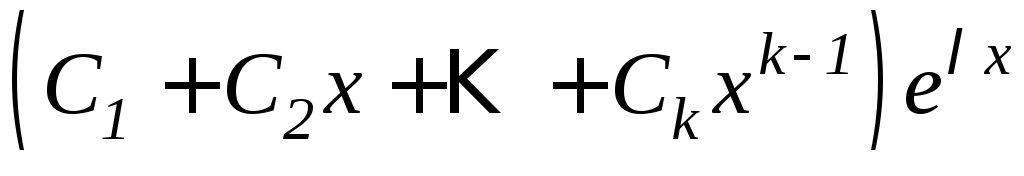 ;
;каждой паре комплексных сопряженных простых корней
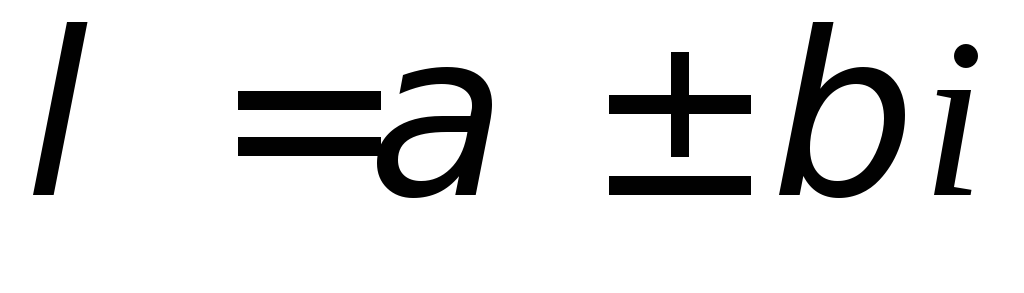 в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида ;
;каждой паре комплексных сопряженных корней
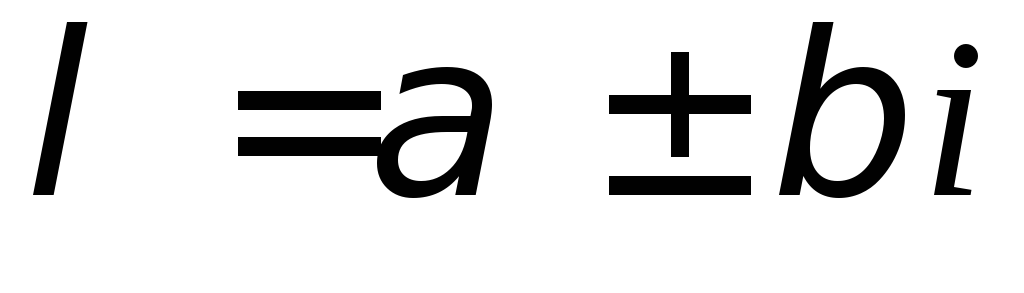 кратности
кратности в общем решении соответствует слагаемое
вида
в общем решении соответствует слагаемое
вида .
.
Пример 18. Решить уравнение
![]() .
.
Решение. Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Соответствующее ему характеристическое уравнение
![]()
имеет действительные
корни
![]() ,
,![]() .
В соответствии с п.1 общее решение
записывается в виде
.
В соответствии с п.1 общее решение
записывается в виде
![]() .
.
Пример 19. Найти решение уравнения
![]() .
.
Решение. Характеристическое уравнение
![]()
имеет равные корни
![]() .
В соответствии с п.2
получаем
общее решение исходного уравнения в
виде
.
В соответствии с п.2
получаем
общее решение исходного уравнения в
виде
![]() .
.
Пример 20. Решить уравнение
![]() .
.
Решение. Имеем:
![]() ,
,
![]() ,
,![]() .
.
На основании п. 3 получаем общее решение уравнения:
![]() .
.
Пример 21. Решить уравнение
![]() .
.
Решение. Здесь характеристическое уравнение
![]()
имеет различные
действительные корни
![]() ,
,![]() ,
,![]() ,
поэтому общим решением исходного
уравнения в соответствии с п.1 будет
,
поэтому общим решением исходного
уравнения в соответствии с п.1 будет
![]() .
.
Пример 22. Найти решение уравнения
![]() .
.
Решение. Имеем соответствующее характеристическое уравнение
![]() ,
,
![]() ,
,![]() .
.
Поэтому согласно п.4 общее решение имеет вид
![]() .
.
Дифференциальное уравнение
![]() (11.15)
(11.15)
называется линейным неоднородным уравнением с постоянными коэффициентами.
Общее решение уравнения (11.15) определяется формулой
![]() ,
,
где
![]() - общее решение соответствующего
однородного уравнения (11.13), а
- общее решение соответствующего
однородного уравнения (11.13), а![]() - частное решение данного неоднородного
уравнения.
- частное решение данного неоднородного
уравнения.
В общем случае частное решение уравнения (11.15) может быть найдено с помощью метода вариации постоянных (метода Лагранжа). Если
![]()
общее решение однородного уравнения (11.13), то общее решение неоднородного уравнения (11.15) ищут в виде
![]() .
.
Функции
![]() ,
,![]() ,
…,
,
…,![]() находят из решения системы уравнений:
находят из решения системы уравнений:
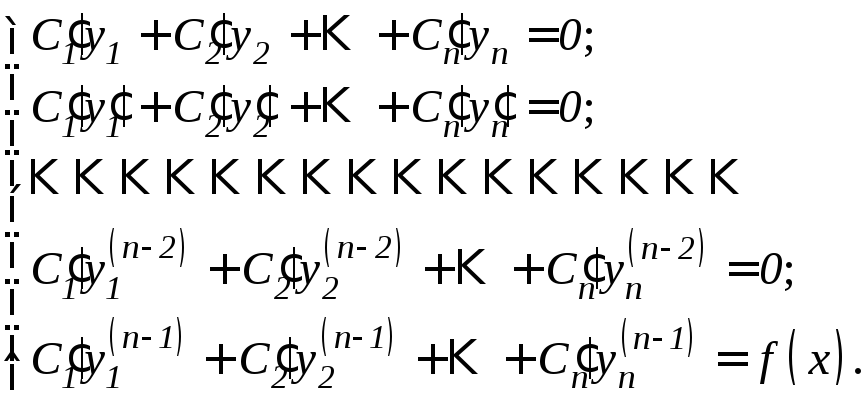 (11.16)
(11.16)
Пример 23. Найти решение задачи Коши
![]()
с начальными
условиями
![]() ,
,![]() .
.
Решение. Соответствующее однородное уравнение имеет вид
![]() .
.
Имеем характеристическое уравнение
![]() .
.
Ему соответствуют
корни
![]() и
и![]() .
Тогда общее решение однородного
уравнения:
.
Тогда общее решение однородного
уравнения:
![]() .
.
Применим метод вариации постоянных. Для этого решение данного неоднородного уравнения ищем в виде
![]() .
.
Для определения
функций
![]() ,
,![]() записываем систему уравнений (11.16):
записываем систему уравнений (11.16):
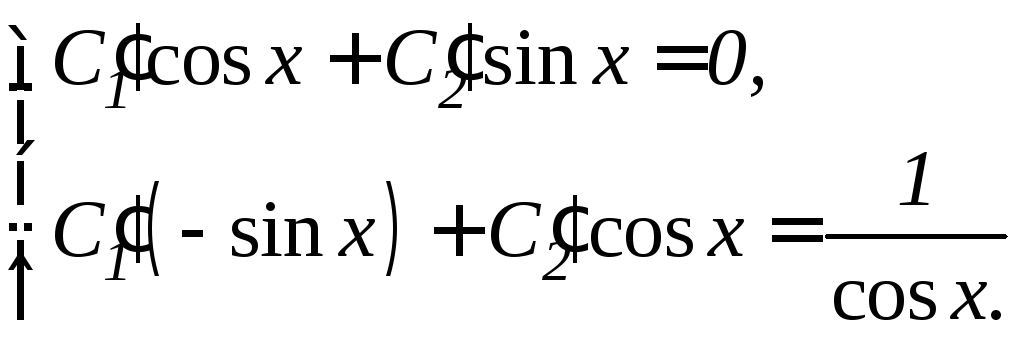
Решая ее (т.к.
решение ищем в окрестности точки
![]() ,
то
,
то![]() ),
получаем
),
получаем
![]() ,
,
![]() .
.
Интегрируя, находим
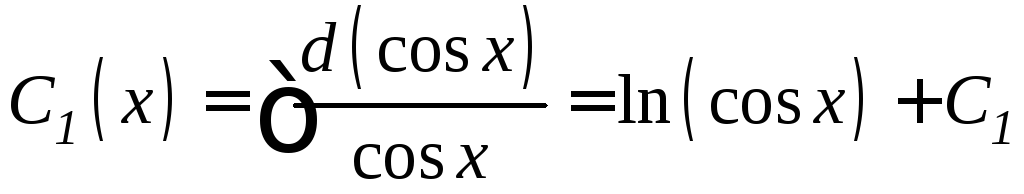 ,
,
![]() .
.
Записываем полученное общее решение данного неоднородного уравнения
![]() .
.
Используя начальные
условия, определяем константы
![]() и
и![]() .
Т.к.
.
Т.к.
![]() ,
,
то
![]() .
Т.к.
.
Т.к.
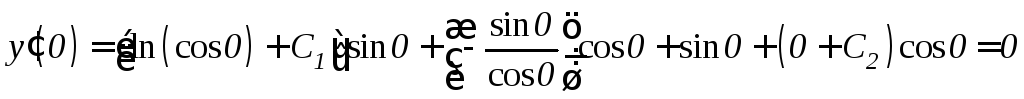 ,
,
то
![]() .
Таким образом, решением задачи Коши
является
.
Таким образом, решением задачи Коши
является
![]() .
.
В простейших случаях частное решение может быть найдено с помощью метода неопределенных коэффициентов. Этот метод применим только в том случае, если правая часть уравнения (11.15) имеет специальный вид. Укажем возможные случаи и соответствующие им виды частных решений:
 ,
где
,
где
 - полином от
- полином от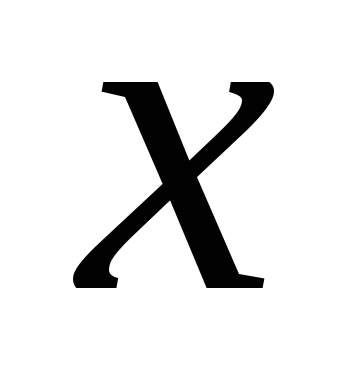 ,
который может, в частности, быть заданным
постоянным числом, отличным от нуля.
Тогда частное решение неоднородного
уравнения (11.15) можно найти в виде
,
который может, в частности, быть заданным
постоянным числом, отличным от нуля.
Тогда частное решение неоднородного
уравнения (11.15) можно найти в виде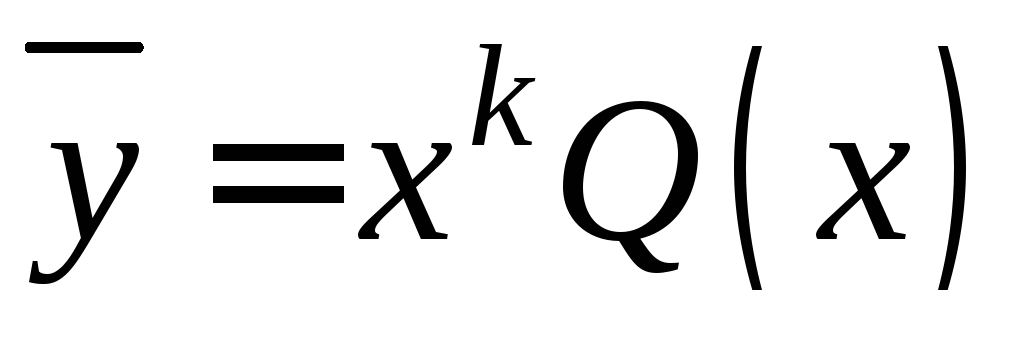 ,
где
,
где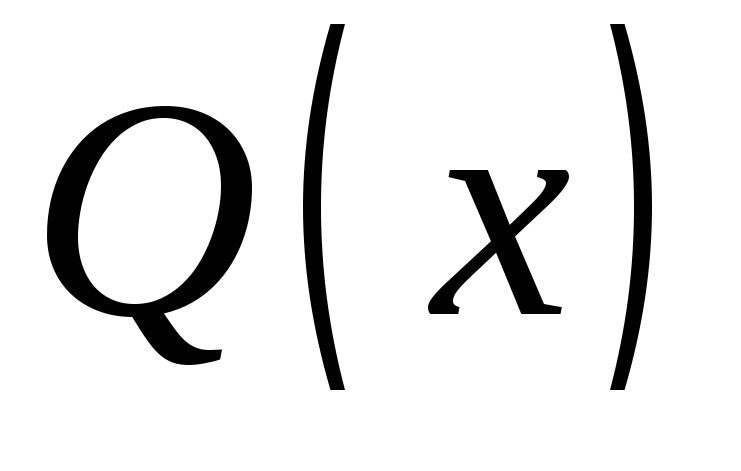 - полином той же степени, что и
- полином той же степени, что и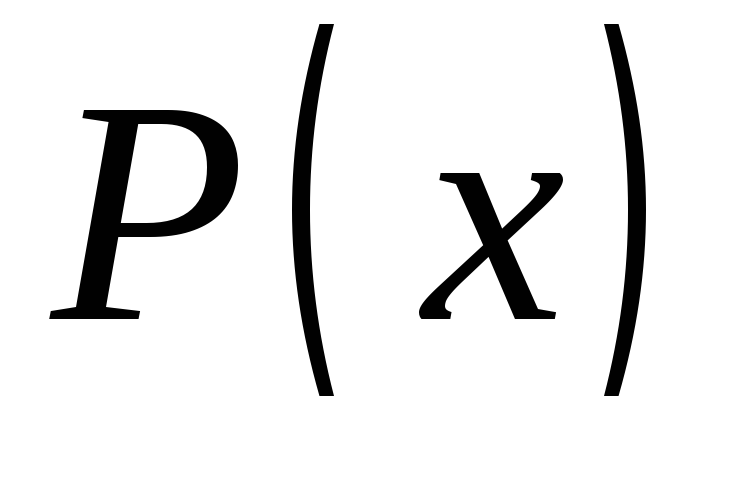 ,
но с неопределенными коэффициентами,
а
,
но с неопределенными коэффициентами,
а - число корней характеристического
уравнения, равных нулю.
- число корней характеристического
уравнения, равных нулю.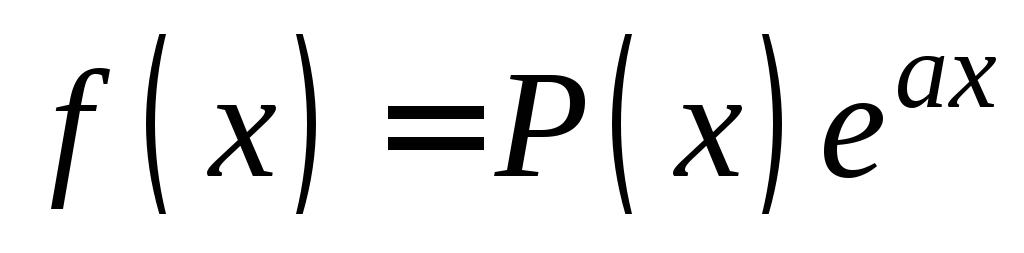 ,
где
,
где
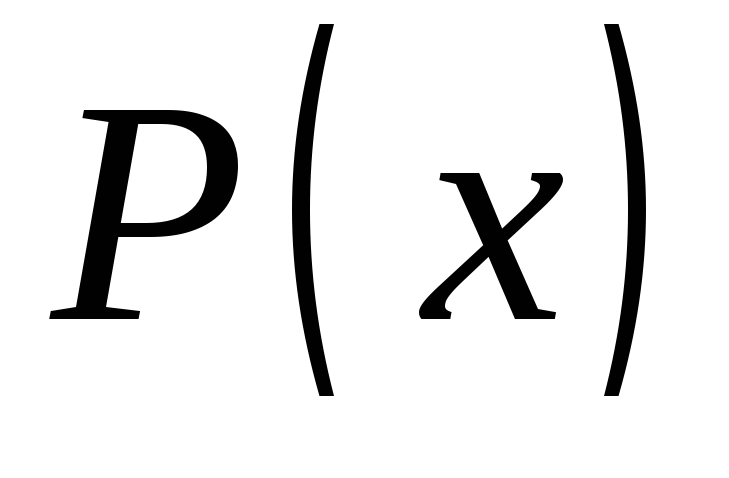 - полином от
- полином от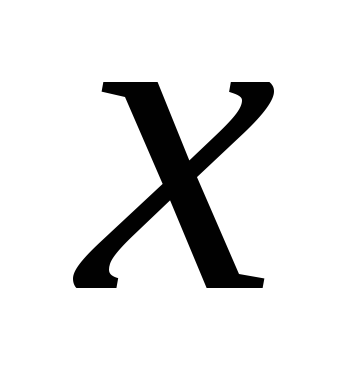 .
Тогда частное решение следует искать
в виде
.
Тогда частное решение следует искать
в виде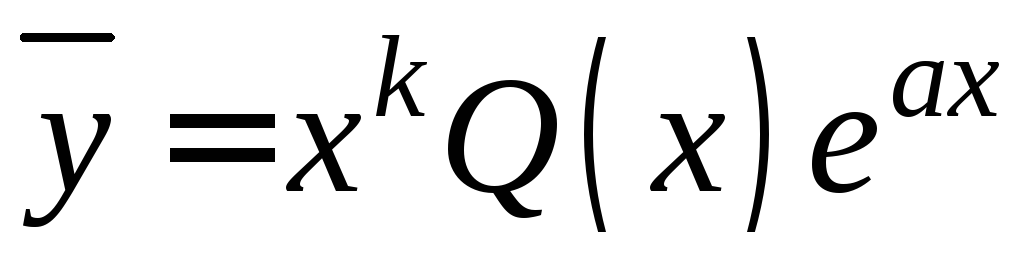 ,
где
,
где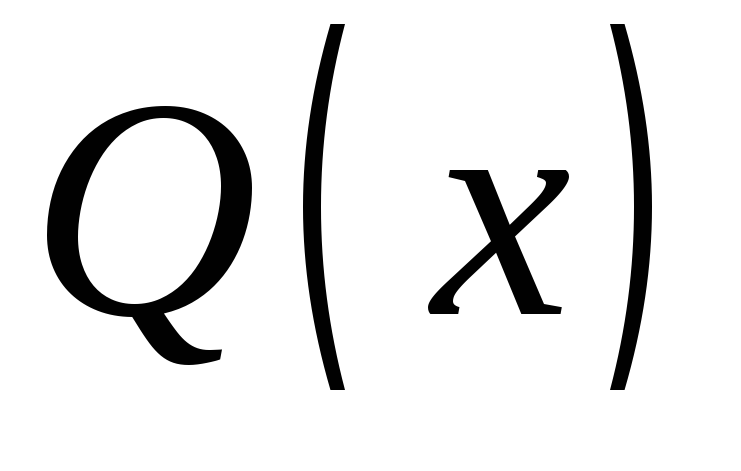 - полином той же степени, что и
- полином той же степени, что и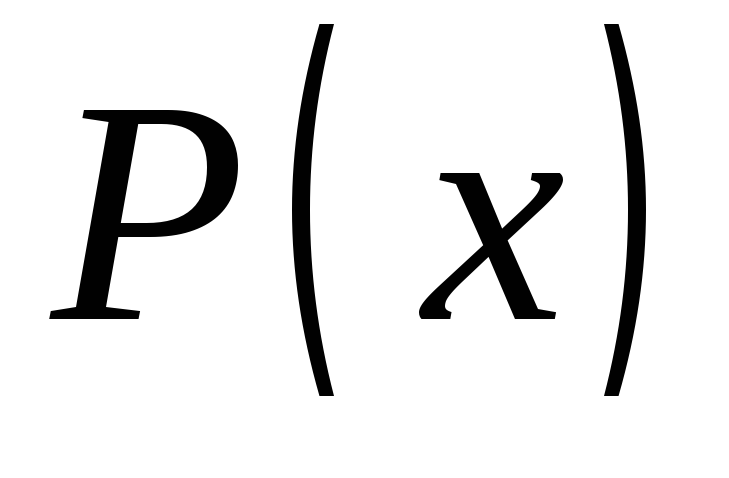 ,
а
,
а - число корней характеристического
уравнения, равных
- число корней характеристического
уравнения, равных .
. ,
где
,
где
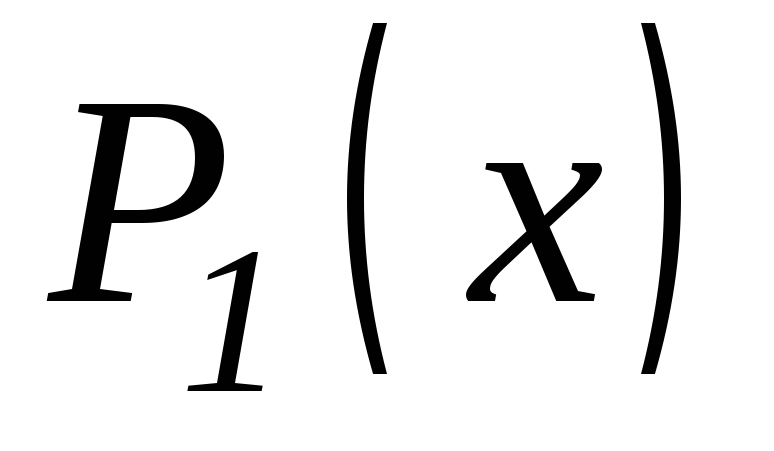 и
и - полиномы от
- полиномы от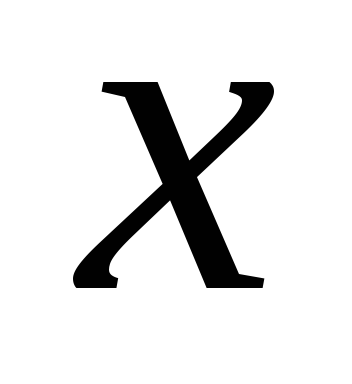 .
(Эти полиномы, в частности, могут быть
постоянными числами, и один из них –
тождественным нулем). Пусть
.
(Эти полиномы, в частности, могут быть
постоянными числами, и один из них –
тождественным нулем). Пусть - наивысшая из степеней полиномов
- наивысшая из степеней полиномов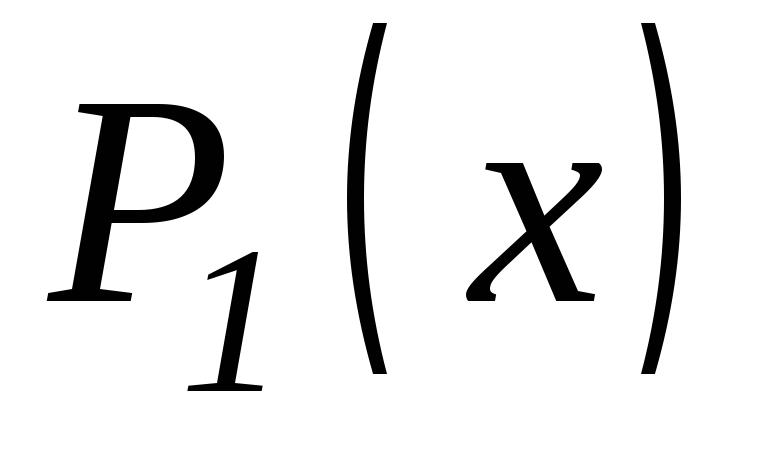 и
и .
Тогда частное решение следует искать
в виде
.
Тогда частное решение следует искать
в виде
![]() ,
,
где
![]() ,
,![]() - полиномы степени
- полиномы степени
![]() с неопределенными коэффициентами,
с неопределенными коэффициентами,![]() - число корней характеристического
уравнения, равных
- число корней характеристического
уравнения, равных![]() .
.
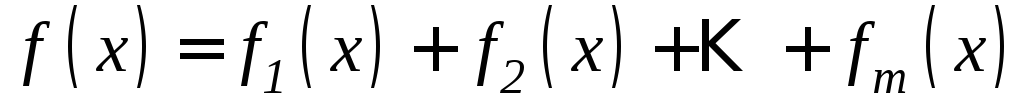 ,
где
,
где
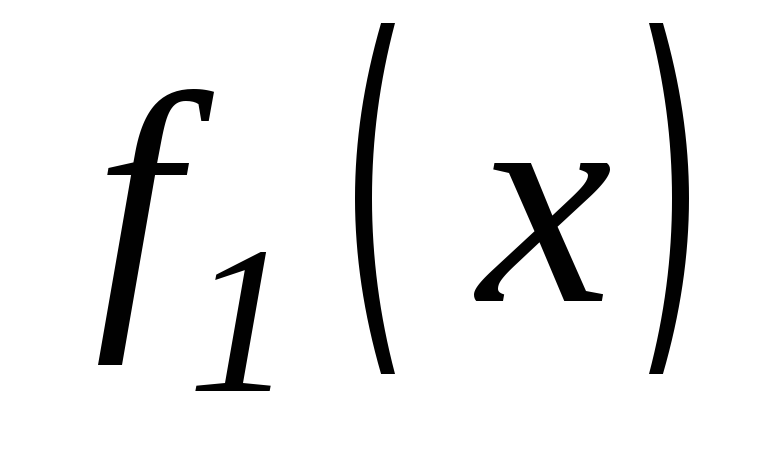 ,
, ,
…,
,
…,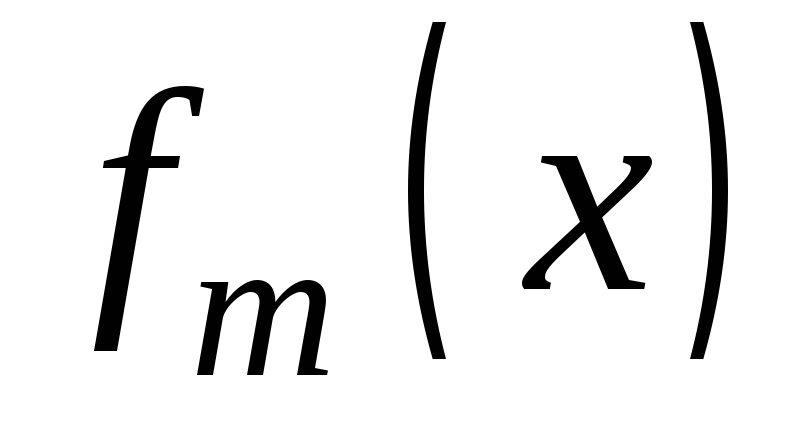 - функции вида, рассмотренного в п.п.
1-3. Если
- функции вида, рассмотренного в п.п.
1-3. Если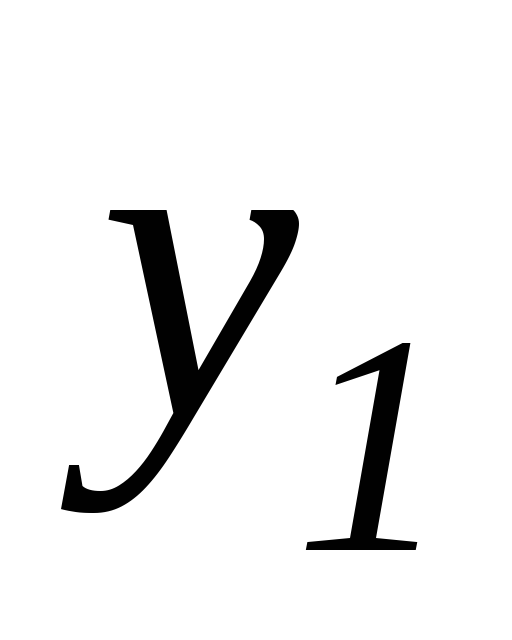 ,
,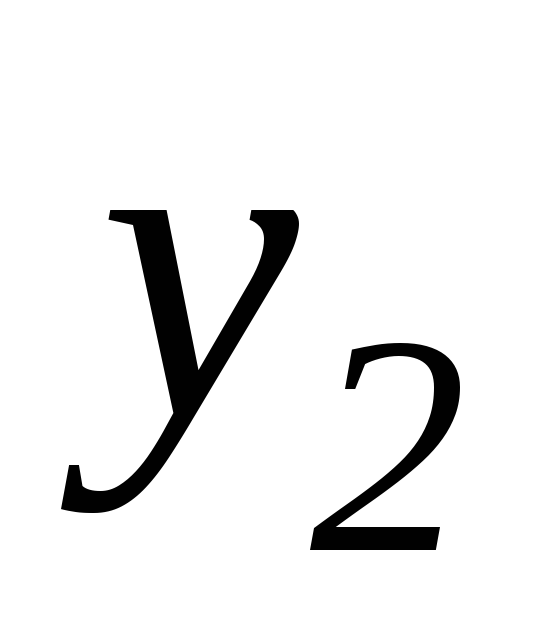 ,
…,
,
…,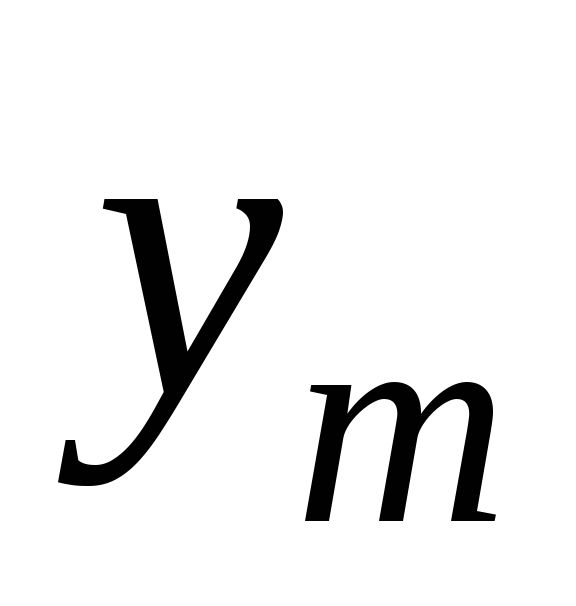 - частные решения, соответствующие
функциям
- частные решения, соответствующие
функциям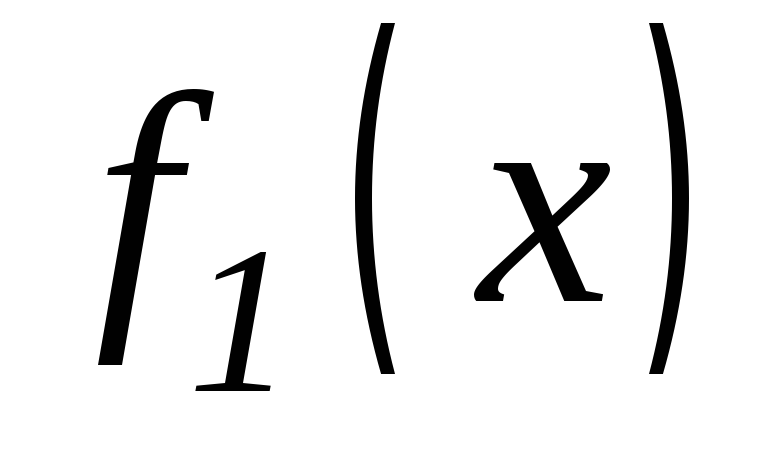 ,
,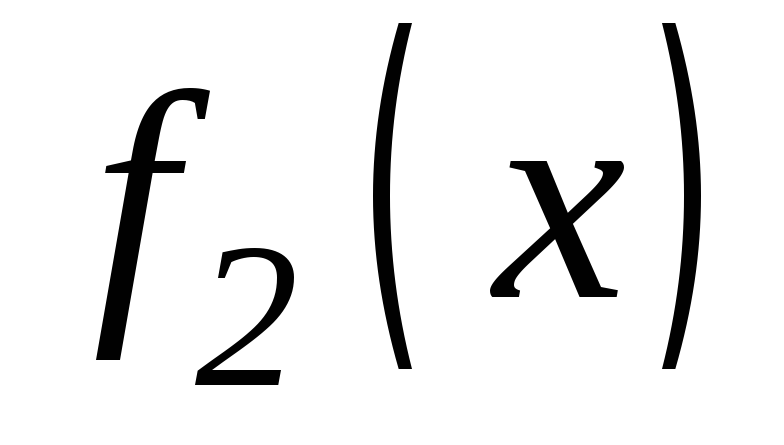 ,
…,
,
…,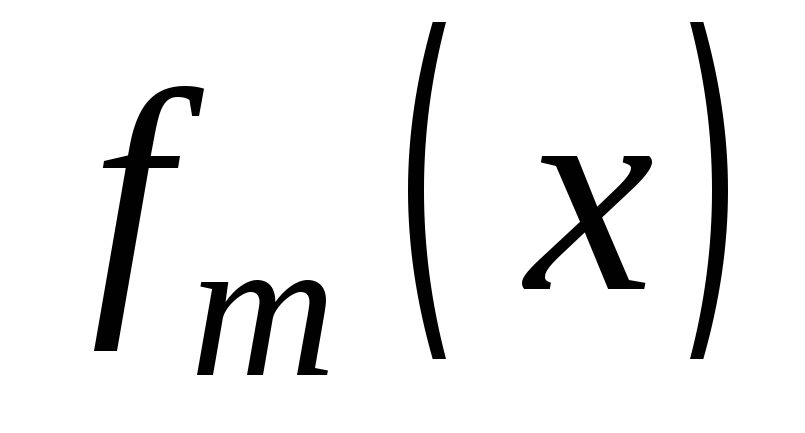 ,
,
то
![]() является частным решением уравнения
(11.15).
является частным решением уравнения
(11.15).
Пример 24. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение, соответствующее однородному уравнению имеет вид
![]() .
.
Его корнями являются
![]() .
Им соответствует общее решение
.
Им соответствует общее решение
![]() .
.
Согласно п.1 частное решение ищем в виде
![]() ,
,
где
![]() и
и![]() - неизвестные коэффициенты. Дифференцируя
- неизвестные коэффициенты. Дифференцируя![]() дважды и подставляя
дважды и подставляя![]() ,
,![]() ,
,![]() ,
находим
,
находим
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях
![]() в обеих частях равенства:
в обеих частях равенства:
![]() :
:
![]() ;
;
![]() :
:
![]() ,
,
находим
![]() ,
,![]() .
Итак, частное решение данного уравнения
имеет вид
.
Итак, частное решение данного уравнения
имеет вид![]() ,
а его общее решение
,
а его общее решение
![]() .
.
Пример 25. Найти общее решение дифференциального уравнения
![]() .
.
Решение.
Найдем
общее решение
![]() соответствующего однородного уравнения
соответствующего однородного уравнения
![]() .
.
Решая отвечающее ему характеристическое уравнение
![]() ,
,
получаем корни
![]() ,
,![]() .
Следовательно,
.
Следовательно,
![]() .
.
Перейдем к отысканию
частного решения
![]() исходного уравнения. Здесь правая часть
имеет вид
исходного уравнения. Здесь правая часть
имеет вид![]() ,
т.е. соответствует п. 2 с
,
т.е. соответствует п. 2 с![]() ,
,![]() .
Т.к. число
.
Т.к. число![]() не является корнем характеристического
уравнения, тоk
=0
не является корнем характеристического
уравнения, тоk
=0
![]() .
Следовательно, частное решение
.
Следовательно, частное решение![]() нужно искать в виде
нужно искать в виде
![]() ,
,
где
![]() ,
,![]() и
и![]() - некоторые неизвестные коэффициенты.
Для их отыскания воспользуемся тем, что
- некоторые неизвестные коэффициенты.
Для их отыскания воспользуемся тем, что![]() должно быть решением исходного уравнения.
Найдем
должно быть решением исходного уравнения.
Найдем
![]() и
и
![]() :
:
![]() ,
,
![]()
![]() ;
;
теперь подставим эти выражения в исходное уравнение:
![]()
![]() .
.
Сокращая обе части
полученного равенства на
![]() и группируя члены при одинаковых степенях
и группируя члены при одинаковых степенях![]() ,
в результате получим
,
в результате получим
![]() .
.
Это равенство
тождественно выполняется только тогда,
когда коэффициенты при одинаковых
степенях
![]() в обеих частях равны между собой. Итак,
для отыскания коэффициентов
в обеих частях равны между собой. Итак,
для отыскания коэффициентов![]() ,
,![]() и
и![]() имеем следующую систему уравнений:
имеем следующую систему уравнений:
![]() :
:
![]() ;
;
![]() :
: ![]() ;
;
![]() :
:
![]() .
.
Решая эту систему,
найдем
![]() ,
,![]() ,
,![]() .
Таким образом, получаем искомое частное
решение
.
Таким образом, получаем искомое частное
решение
![]() .
.
Теперь можно записать общее решение исходного уравнения:
![]() .
.
Пример 26. Найти решение уравнения
![]() ,
,
удовлетворяющего
краевым условиям
![]() ,
, .
.
Решение. Характеристическое уравнение
![]()
имеет корни
![]() ,
,![]() ,
поэтому общее решение соответствующего
однородного уравнения
,
поэтому общее решение соответствующего
однородного уравнения
![]() .
.
Частное решение
![]() ,
согласно п.3 следует искать в виде
,
согласно п.3 следует искать в виде
![]() ,
,
т.к.
![]() ,
,![]() ;
;![]() является простым корнем характеристического
уравнения, поэтому
является простым корнем характеристического
уравнения, поэтому![]() ;
кроме того,
;
кроме того,![]() .
Итак, дифференцируя
.
Итак, дифференцируя![]() дважды и подставляя производные в
исходное уравнение, получим
дважды и подставляя производные в
исходное уравнение, получим
![]() .
.
Приведя подобные, получим
![]() ;
;
Приравнивая
коэффициенты при
![]() и
и![]() в правой и левой частях полученного
равенства, имеем
в правой и левой частях полученного
равенства, имеем
![]() :
:
![]() ,
,
![]() :
:
![]() ,
,
т.е.
![]() ,
,![]() .
Следовательно, частное решение исходного
уравнения имеет вид
.
Следовательно, частное решение исходного
уравнения имеет вид
![]() ,
,
а общее решение исходного уравнения
![]() .
.
Постоянные
![]() и
и![]() найдем, используя краевые условия.
Имеем
найдем, используя краевые условия.
Имеем
![]() .
.
и, далее,
![]() ,
,
![]() ,
,
 ,
,
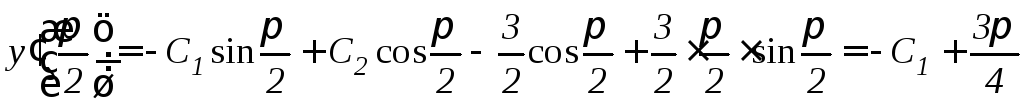 .
.
Таким образом,
![]() ,
,
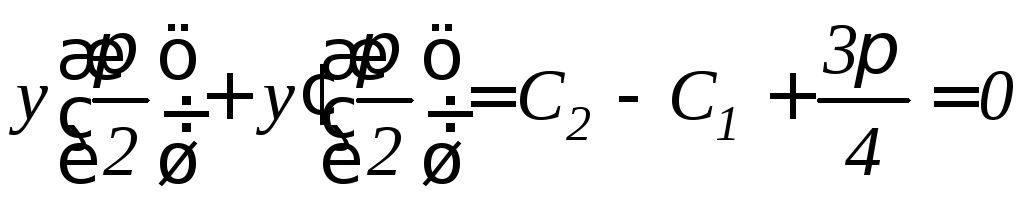 ,
,
откуда получим систему уравнений
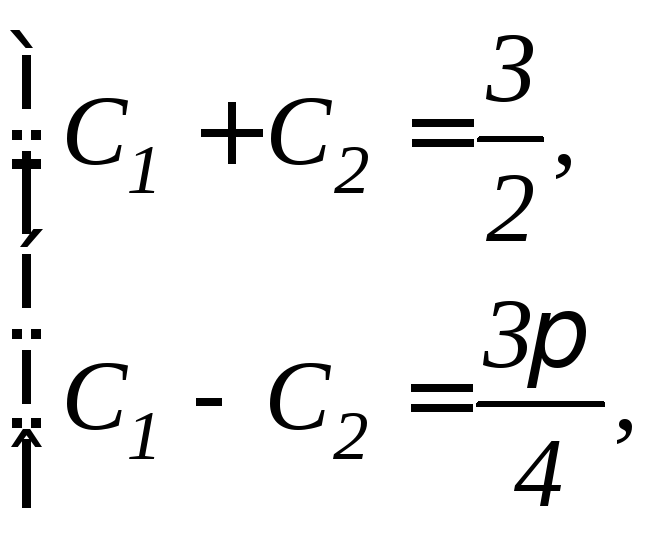
решая которую,
находим
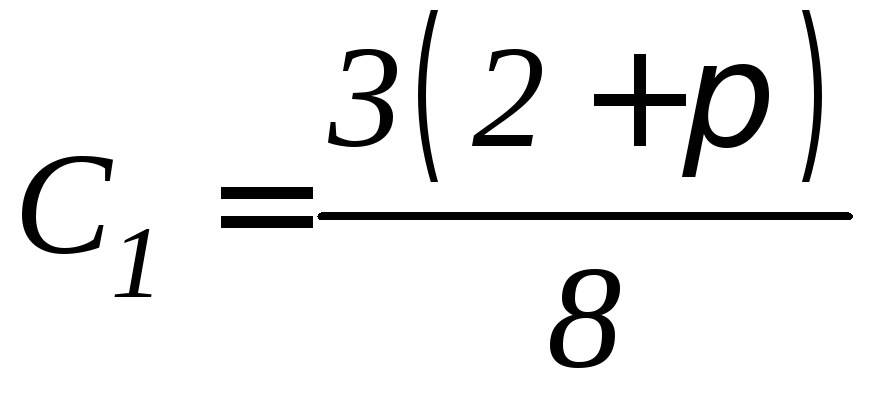 ,
,
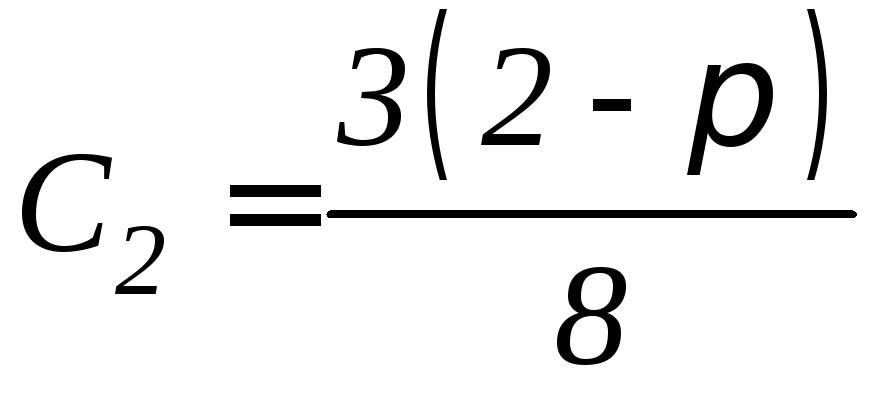 .
Таким образом, решение исходного
уравнения, удовлетворяющее поставленным
краевым условиям имеет вид
.
Таким образом, решение исходного
уравнения, удовлетворяющее поставленным
краевым условиям имеет вид
![]() .
.
Пример 27. Найти общее решение дифференциального уравнения
![]() .
.
Решение.
Находим
сначала
![]() .
Характеристическое уравнение
.
Характеристическое уравнение
![]()
имеет корни
![]() ,
,![]() ,
поэтому
,
поэтому
![]() .
.
Переходим к
нахождению
![]() .
Здесь правая часть
.
Здесь правая часть![]() исходного уравнения представляет собой
сумму функций
исходного уравнения представляет собой
сумму функций![]() и
и![]() .
Согласно п.4 будем искать частные
решения
.
Согласно п.4 будем искать частные
решения![]() ,
,![]() для каждой из функций в отдельности.
для каждой из функций в отдельности.
Функция
![]() соответствует п.1 при
соответствует п.1 при![]() и
и![]() .
Значит
.
Значит
![]() .
.
Дифференцируя, находим
![]() ,
,
![]() ,
,
подставляя
![]() и
и![]() в левую часть исходного уравнения и
приравнивая полученное выражение к
в левую часть исходного уравнения и
приравнивая полученное выражение к![]() ,
получим
,
получим
![]() ,
,
откуда
![]() :
:
![]() ,
,
![]() :
:
![]() ,
,
или
![]() ,
,![]() .
Таким образом,
.
Таким образом,
 .
.
Функция
![]() соответствует п.3 при
соответствует п.3 при![]() ,
,![]() ,
,![]() .
Поэтому частное решение ищем в виде
.
Поэтому частное решение ищем в виде
![]() .
.
Дифференцируя, находим
![]()
![]()
![]()
![]() .
.
Подставляя
![]() и
и![]() в левую часть исходного уравнения и
приравнивая полученное выражение к
в левую часть исходного уравнения и
приравнивая полученное выражение к![]() ,
имеем
,
имеем
![]()
или
![]() ,
,
откуда
![]() :
:
![]() ,
,
![]() :
:
![]() ,
,
т.е.
![]() ,
,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Итак, общее решение исходного уравнения запишется следующим образом:
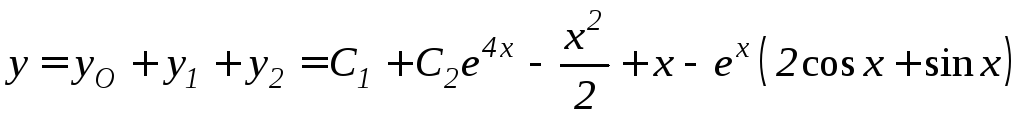 .
.
