Решение вариационной задачи, функционал которой представляется кратным интегралом

Ход рассуждений для определённого, двойного и тройного интегралов одинаков. Приведём эти рассуждения для двойного интеграла (рис. 1). Рассмотрим функционал

.

З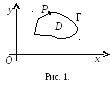десь.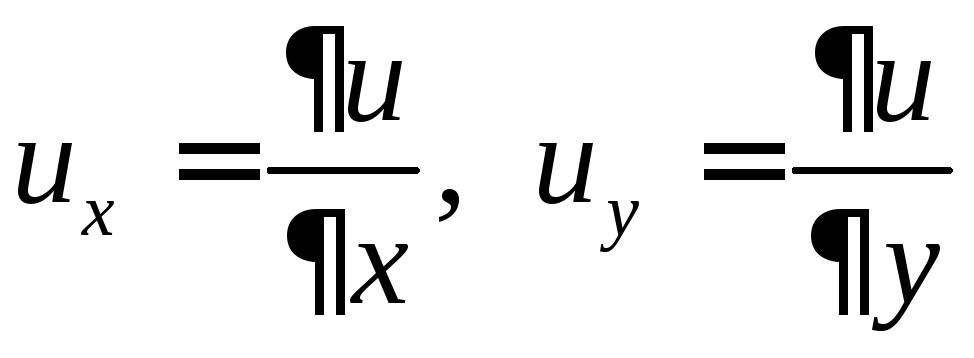

Вариационная задача:

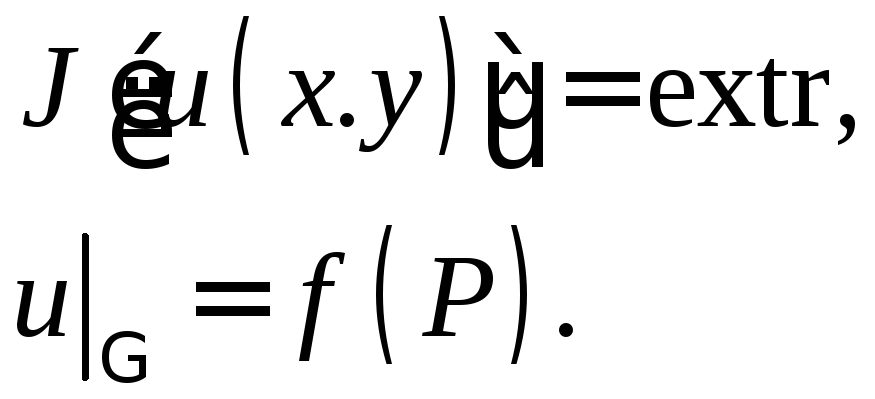(6)

Здесь Γ – граница области D. Предполагаем, что Γ непрерывна и имеет непрерывные производные 1-го и 2-го порядков по своим аргументам; .

Пусть — решение задачи (6). Образуем функции сравнения

,

причём . Тогда, очевидно,и.

Рассмотрим разность

.

Отсюда получаем необходимое условие экстремума

,

или, в явном виде,

.

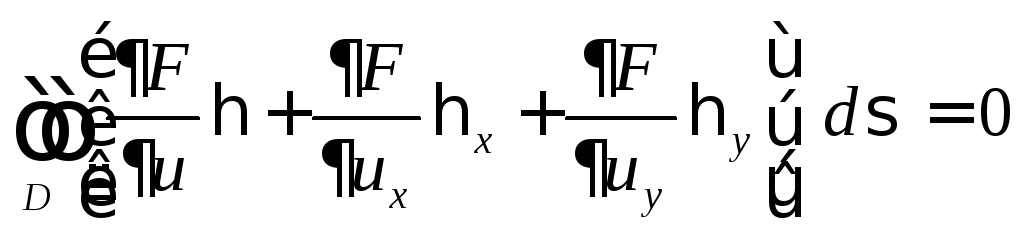Исключим . Для этого введём функцию η под знак производной:

,

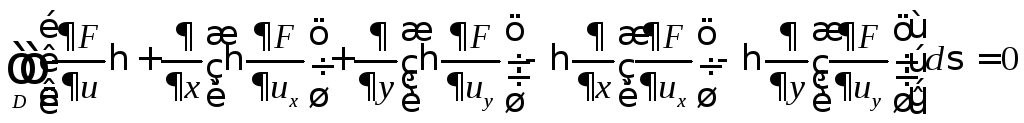откуда

.

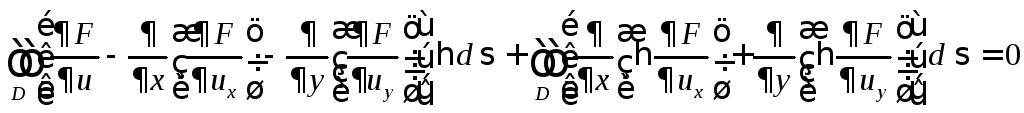Воспользуемся известной формулой Грина

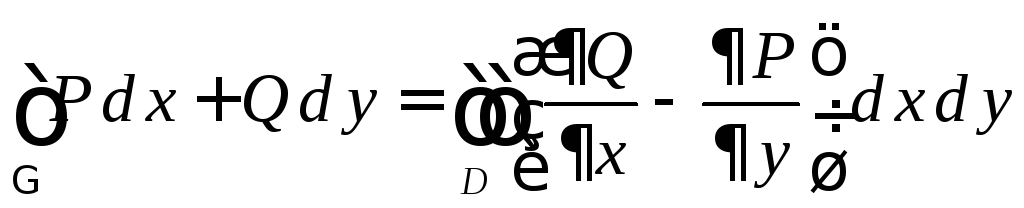
для второго интеграла в последнем равенстве. Получим:

.

А так как , то получаем уравнение Эйлера в следующем виде:

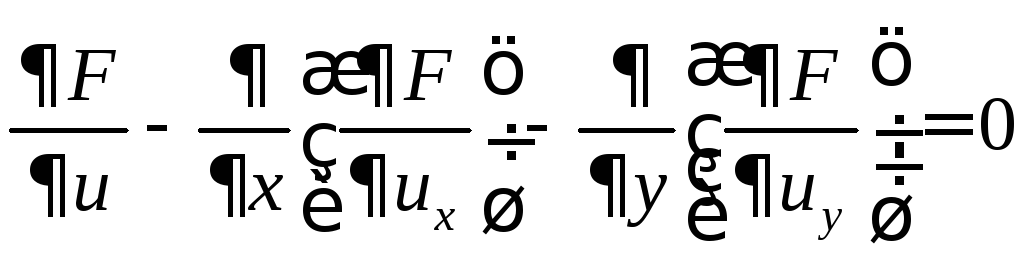. (7)

Уравнение (7) — дифференциальное уравнение второго порядка в частных производных. В случае, когда , мы имеем вариационную задачу для функционала

,

а соответствующее уравнение Эйлера будет таким:

.

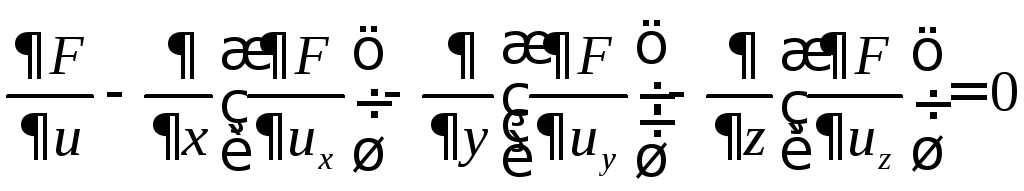Прямые методы вариационного исчисления Конечно-разностный метод Эйлера

Пусть дана простейшая вариационная задача: найти экстремум функционала

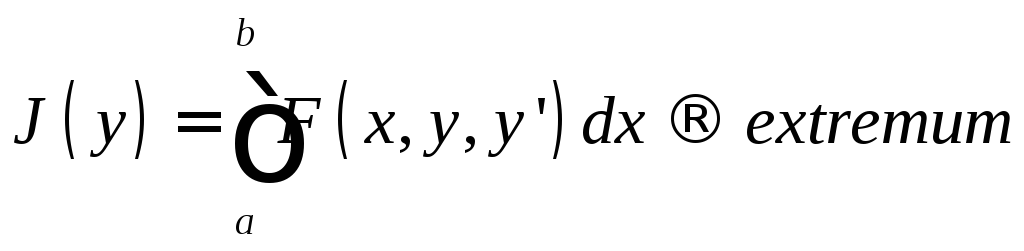(8)

с заданными граничными условиями:

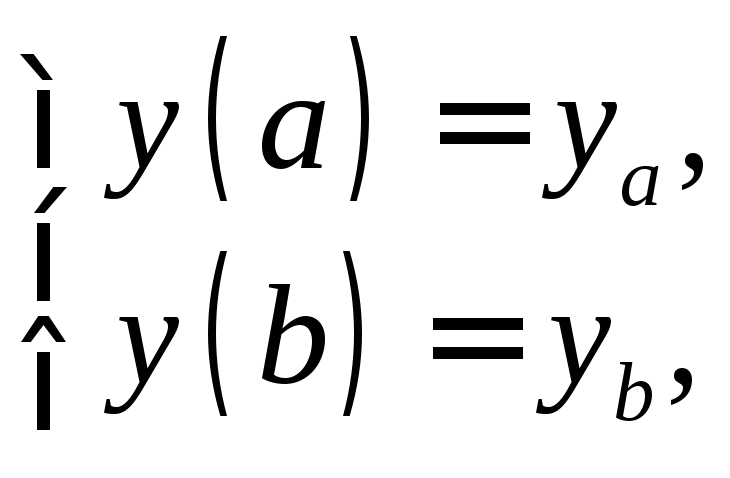(9)

где F(x, y, y) — непрерывная функция трёх переменных и дифференцируемая функция двух своих последних аргументов.

Решаем задачу методом Эйлера – значения функционала (8) рассматриваются не на произвольных, допустимых в данной вариационной задаче кривых, а лишь на ломаных, составленных из заданного числа N прямолинейных звеньев, с заданными абсциссами вершин

, где .

На этих ломаных функционал (8) превращается в функцию ординатвершин ломаной. Ординатывыбираются так, чтобы функциядостигала экстремума, т. е. они определяются из системы уравнений

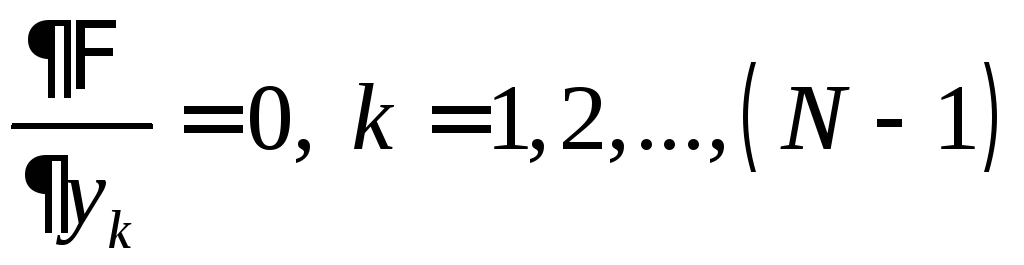
(ординаты иизвестны из граничных условий).

Метод Ритца

Метод Ритца представляет собой один из методов построения минимизирующей последовательности для функционала.

Решение уравнения

, (6)

где А — положительный оператор, сводится к нахождению минимума функционала

, (7)

где скалярное произведение

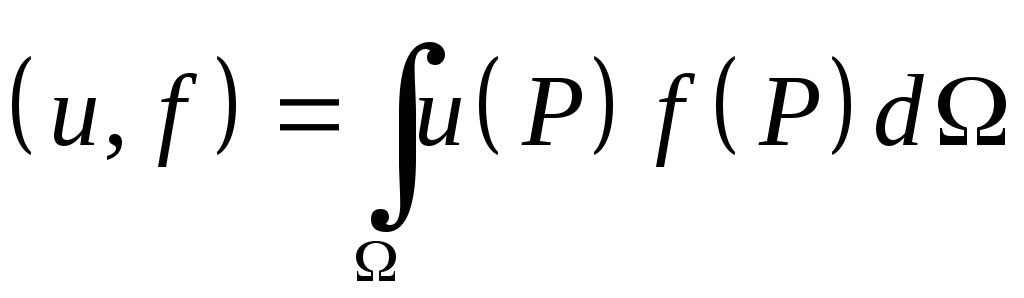. (8)

Эту последнюю задачу будем приближенно решать следующим образом. Выберем последовательность

, (9)

координатных функций, принадлежащих области определения оператора D_A; подчиним эту последовательность двум условиям:

1. последовательность (9) полна по энергии;

2. при любом n функции 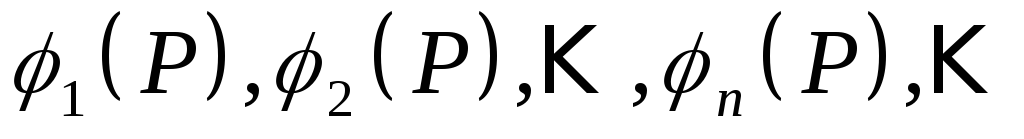линейно независимы.

Построим линейную комбинацию первых n координатных функций

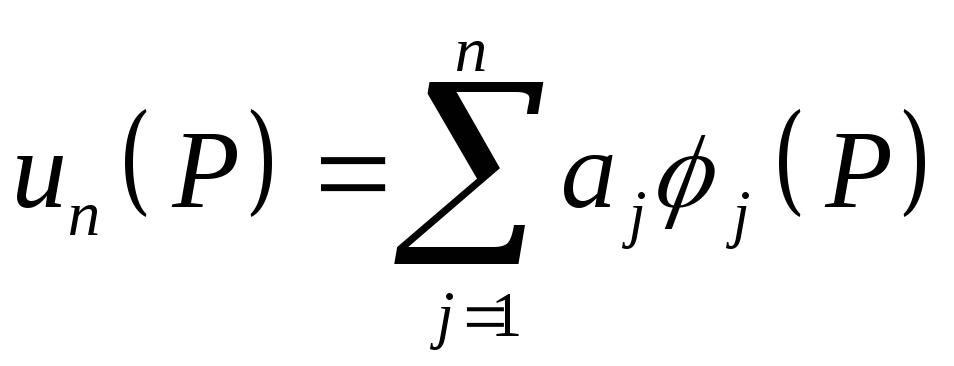(10)

с произвольными численными коэффициентами a_j. Подставим u_n(P) вместо u(P) в функционал (7); это превратит F(u) в функцию n независимых переменных a₁, a₂, …, a_n:

. (11)

Выберем коэффициенты a_j так, чтобы функция (11) приняла минимальное значение. Функция (11) достигает минимума при тех значениях независимых переменных, которые обращают в нуль ее первые производные:

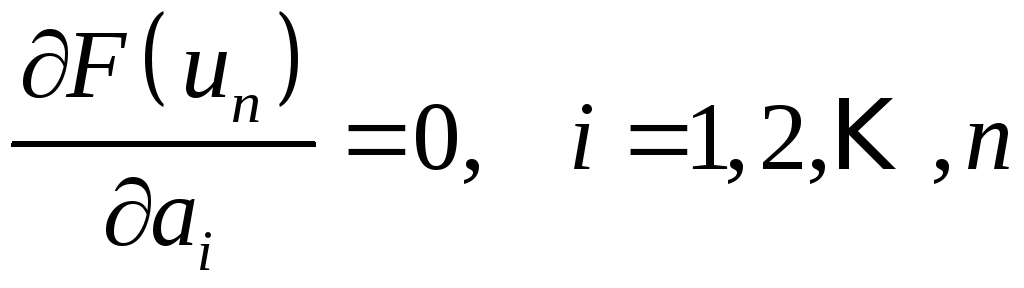. (12)

Уравнения (12) дают, как известно, необходимые условия минимума F(u_n). Однако, используя положительность оператора A, можно доказать, что коэффициенты a_j, удовлетворяющие системе (12), реализуют минимум величины F(u_n).

Соотношения (12) представляют собой систему линейных алгебраических уравнений

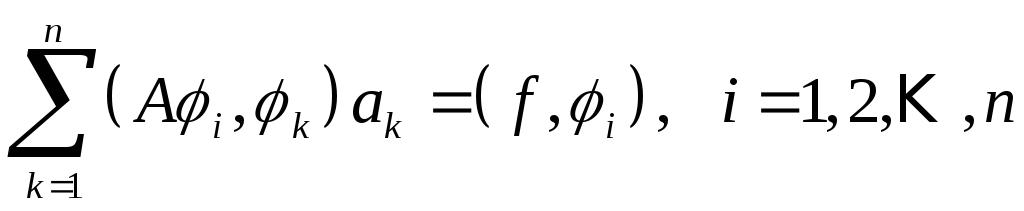. (13)

Определитель системы (13) есть определитель Грамма линейно независимых функций и потому отличен от нуля. Отсюда следует, что система уравнений Ритца всегда разрешима, если оператор А — положительный.

Найдя коэффициенты a₁, a₂, …, a_n и подставив их в (10), получим функцию u_n(P), которую будем называть приближенным решением уравнения (6) по Ритцу.