dm_tema_3

3. Алгебра логики 3.4 Нормальные формы булевых функций

Любую булеву функцию можно представить в виде полинома Жегалкина. Для этого в СДНФ достаточно заменить x íà 1 x,

операцию _ íà .

Пример

f(x1; x2; x3) = (1 x1)x2(1 x3) (1 x1)x2x3 x1(1 x2)x3 x1x2x3 =

=x2 x1x2 x1x3:

3.5 Построение минимальных ДНФ

Определение

ДНФ булевой функции называется минимальной, если общее количество литералов в ней минимально.

Метод Квайна построения минимальной ДНФ.

Пусть булева функция задана в виде СДНФ. На первом этапе выполняем операции склеивания и поглощения

xy _ xy = (x _ x)y = 1y = y;

x_ xy = x(1 _ y) = x1 = x:

Âрезультате получаем сокращ¼нную ДНФ. Элементарные конъюнкции сокращ¼нной ДНФ называются импликантами.

На втором этапе составляем таблицу импликантов. Столбцы таблицы соответствуют конституентам единицы СДНФ, строки импликантам сокращ¼нной ДНФ.

Отмечаем вхождения импликантов в конституенты единицы. Выбираем наименьшее число импликант, дизъюнкция которых сохраняет все конституенты единицы. Получаем тупиковые ДНФ. Минимальная ДНФ выбирается из тупиковых ДНФ.

Пример Пусть булева функция задана СДНФ

f (x1; x2; x3) = x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3:

Построим таблицу склеивания

Сокращ¼нная ДНФ

f (x1; x2; x3) = x1x3 _ x2x3 _ x1x3 _ x1x2 _ x2x3 _ x1x2:

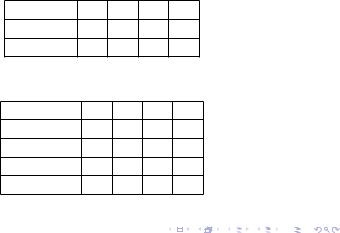
Построим таблицу импликантов

Тупиковые ДНФ

f(x1; x2; x3) =x1x3 _ x1x2 _ x2x3;

f(x1; x2; x3) =x2x3 _ x1x3 _ x1x2

являются минимальными.

Метод карт Карно построения минимальной ДНФ.

Карта Карно это преобразованная таблица значений булевой функции. Карта Карно для функции тр¼х переменных имеет следующий вид

x1 x2x3 11 10 00 01

1

0

Карта Карно для функции четыр¼х переменных

x1x2 x3x4 10 11 01 00

10

11

01

00

В клетках ставятся 0 и 1, соответствующие значениям функции. Единицы, расположенные в соседних клетках (по горизонтали и вертикали) могут склеиваться.

При этом карту можно свернуть по горизонтали и вертикали. Для построения минимальной ДНФ необходимо найти наиболее рациональное покрытие единиц карты Карно.

Пример Для функции

f (x1; x2; x3) = x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3 _ x1x2x3:

карта Карно имеет вид

Минимальные покрытия

f(x1; x2; x3) = x1x2 _ x1x3 _ x2x3;

f(x1; x2; x3) = x1x3 _ x2x3 _ x1x2;

показаны на рисунке

3.6 Контактные и функциональные схемы

Контактная схема представляет собой электрическую цепь, содержащую контакты двух типов: замыкающие и размыкающие.

x

y = x

x¯

y = x¯