Введение в математику

но нуля, следовательно, данная функция общего вида, т. е. не является ни четной, ни нечетной.

Определение 3.4. Функция f(x) называется периодической, åñëè 9 T > 0:

8x 2 D(f) (x + T ) 2 D(f) и f(x + T ) = f(x). Наименьшее из таких чисел T называется периодом функции.

Пример 3.6. Функции sin x, cos x периодические с периодом 2 , а функции tg x, ctg x периодические с периодом .

Пример 3.7. Исследовать функции на периодичность и указать период функции в случае ее периодичности:

1)y = sin 5x;

2)y = sin2 3x.

Решение.

1) Пусть u = 5x, тогда sin 5x = sin u. Известно, что sin(u + 2 ) = sin u. Тогда

41

2) Воспользуемся формулой понижения степени и получим:

Пусть функция y = f(x) определена на множестве D(f) и пусть некоторое множество D1 D(f). Если для любых значений x1; x2 2 D1 из неравенства x1 < x2 следует неравенство:

f(x1) < f(x2), то функция называется строго возрастающей на множестве

D1;

f(x1) f(x2), то функция называется возрастающей на множестве D1;

f(x1) > f(x2), то функция называется строго убывающей на множестве

D1;

f(x1) f(x2), то функция называется убывающей на множестве D1. Возрастающие, строго возрастающие, убывающие и строго убывающие функ-

ции на множестве D1 называются монотонными на этом множестве, а строго возрастающие и строго убывающие строго монотонными.

Например, функция y = f(x), изображенная на следующем рисунке строго убывает на интервале (a; b), строго возрастает на интервале (b; c) и убывает на интервале (c; d).

42

Функция y = f(x), определенная на множестве D, называется ограниченной сверху на этом множестве, если существует число M 2 R такое, что для всех x 2 D выполняется неравенство f(x) M. Если для функции y = f(x), определенной на множестве D, существует число m 2 R такое, что для всех x 2 D выполняется неравенство f(x) m, то она ограниченна снизу на этом

множестве.

Функция y = f(x), определенная на множестве D, называется ограничен-

ной на этом множестве, если она ограничена и сверху, и снизу, т. е. существует такое число C > 0, что для всех x 2 D выполняется неравенство jf(x)j C.

График ограниченной функции лежит между прямыми y = C и y = C. Функцию, не являющуюся ограниченной на множестве D, называют неогра-

ниченной на множестве D. Это означает, что для любого числа C существует x0 2 D такое, что jf(x0)j > C.

Пример 3.8. Выяснить, ограничены или не ограничены функции:

1)y = sin x;

2)y = x2 1;

3)y = x + 1.

Решение.

1)Функция y = sin x является ограниченной, потому что для любого x 2 R выполняется неравенство j sin xj 1.

2) Функция y = x2 1 является ограниченной снизу, поскольку для любого x 2 R выполняется неравенство x2 1 1.

43

3)Функция y = x + 1 не является ограниченной, потому что для любого числа C существует x0 2 R такое, что jx0 + 1j > C. В данном случае достаточно взять x0 = C.

3.3Операции над функциями

Для функции естественным образом определяются арифметические действия:

(f1 f2)(x) = f1(x) f2(x);

(f1 f2)(x) = f1(x) f2(x);

f1 (x) = f1(x): f2 f2(x)

Область определения каждой из новых функций пересечение облаcтей определения функций f1(x) è f2(x). В случае частного необходимо также удалить точки, в которых знаменатель обращается в нуль.

44

Пусть функция y = f(u) определена на множестве D, а функция u = '(x) на множестве D1, причем для любого x 2 D1 соответствующее значение u = '(x) 2 D. Тогда на множестве D1 определена функция y = f('(x)), которая называется сложной функцией (или cуперпозицией заданных функций).

Пример 3.9. Для функций f(x) = cos x1 è g(x) = ln(x2 + 2) найти сложные функции f(g(x)), g(f(x)), f(f(x)), g(g(x)).

Решение. Пусть u = g(x) = ln(x2 + 2), f(u) = cos u1. 1

Тогда f(g(x)) = cos ln(x2 + 2). Аналогичным образом получаем, что

p

Решение. Имеем: f(u) = 3 u,u(v) = log2 v, v(x) = sin x.

Пусть задана функция y = f(x) с областью определения D и множеством зна- чений E. Если каждому значению y 2 E соответствует единственное значение x 2 D, то определена функция x = '(y) с областью определения E и множе-

ством значений D. Такая функция '(y) называется обратной к функции f(x) и записывается в виде: x = '(y) = f 1(y). Функции y = f(x) и x = '(y) в этом

случае называют взаимно обратными.

Чтобы найти функцию x = '(y), обратную к функции y = f(x), достаточно решить уравнение f(x) = y относительно x (если это возможно). Если аргумент

обратной функции обозначить, как обычно, через x, а значение функции через y, то взаимно обратные функции можно записывать в виде y = f(x) и y = f 1(x).

Для взаимно обратных функций при любом x из области определения D

справедливо равенство:

f 1(f(x)) = x:

Из определения обратной функции вытекает, что функция y = f(x) имеет обратную тогда и только тогда, когда функция f(x) задает взаимно однозначное

45

соответствие между множествами D и E, т. е. каждому элементу множества D соответствует ровно один элемент множества E, при этом, определено обратное соответствие, при котором каждому элементу множества E соответствует ровно один элемент множества D. Отсюда следует, что любая строго монотон-

ная функция имеет обратную. При этом если функция возрастает (убывает), то

обратная функция также возрастает (убывает).

Заметим, что графики взаимно обратных функций y = f(x) и y = f 1(x)

симметричны относительно биссектрисы первого и третьего координатных углов (т. е. относительно прямой y = x).

Пример 3.11. Определить, какие из перечисленных функций имеют обратные. Найти соответствующие обратные функции.

x

2) Функция y = f(x) = e2 , определенная на всей числовой оси, возрастает на

x

своей области определения. Выражая x из равенства y = e2 , получаем, что ln y = x2 и x = 2 ln y. Следовательно, f 1(x) = 2 ln x.

46

3)Заметим, что для функции y = x4, определенной на всей числовой оси, обратной не существует, т. к. одному значению y соответствует два значения x

(òàê, åñëè y = 1, òî x1 = 1 è x2 = 1). Однако, если рассмотреть данную

функцию, определенную на интервале [0; +1), то в этом случае обратной p

является функция y = 4 x. Значит, для функции y = f(x) = x4, x 2 [0; +1) p

обратной является функция f 1(x) = 4 x.

3.4Основные элементарные функции и их графики. Элементарные функции

Основными элементарными функциями называют следующие функции: постоянная функция y = C (C 2 R), степенная функция y = x ( 2 R), показа-

тельная функция y = ax (a > 0, a 6= 1), логарифмическая функция y = loga x (a > 0, a 6= 1), тригонометрические функции y = sin x, y = cos x, y = tg x,

47

y = ctg x и обратные тригонометрические функции y = arcsin x, y = arccos x, y = arctg x, y = arcctg x. Напомним их графики и некоторые свойства.

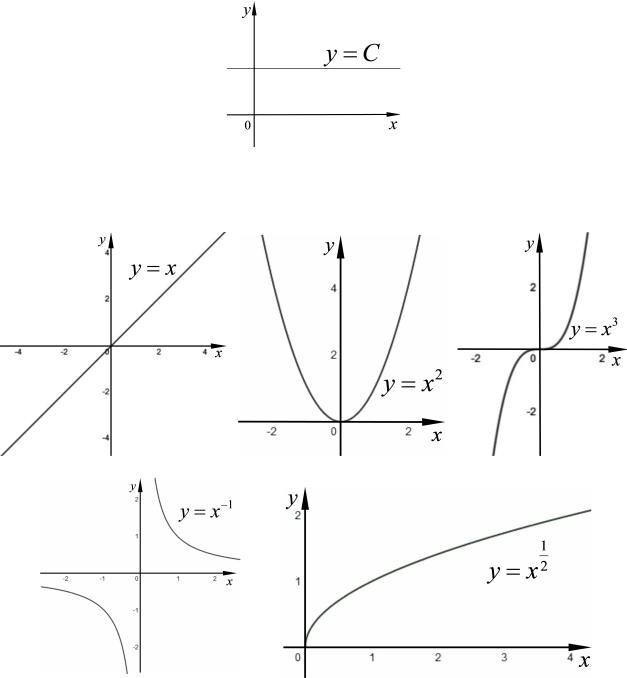
1)Постоянная функция y = C (C 2 R). Графиком является прямая, параллельная оси Ox (горизонтальная прямая), проходящая через точку (0; C) на оси Oy.

2)Степенная функция y = x ( 2 R). Область определения и свойства степенной функции существенно зависят от показателя степени .

3)Показательная функция y = ax (a > 0, a 6= 1). Область определения показательной функции D(y) = R, множество значений E(y) = (0; +1).

48

4) Логарифмическая функция y = loga x (a > 0, a 6= 1). Область определения логарифмической функции D(y) = (0; +1), множество значений

E(y) = R.

5) Тригонометрические функции y = sin x, y = cos x, y = tg x, y = ctg x.

49

6) Обратные тригонометрические функции y = arcsin x, y = arccos x,

y = arctg x, y = arcctg x.

50