Пример

8

Пример 2.2. Задача о производстве красок.  Фабрика производит два вида красок К₁ и К₂. Продукция обеих видов поступает в оптовую продажу. Для производства красок используются два вида сырья А и В. Максимально возможные суточные запасы сырья составляют 6 и 8 т соответственно.

Расходы сырья А и В на 1 т соответствующих красок и максимально возможный запас приведены в таблице. 

Вид сырья	Расход сырья (в тоннах) на 1 тонну краски		Запасы сырья
	К1	К2
А	1	2	6
В	2	1	8

Изучение рынка сбыта показало, что суточный спрос на краску К₂ никогда не превышает спроса на краску К₁ более чем на 1 т.  Кроме этого установлено, что спрос на краску К₂ никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. долл. для краски К1 и 2 тыс. долл. для краски К₂.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Решение

. Строим экономико-математическую модель задачи.

Вводим управляющие переменные: – суточный объем производства краски К₁ (в тоннах), – суточный объем производства краски К₂ (в тоннах).

Записываем систему ограничений:

, (5), (6).

, тыс. долл. – доход от реализации продукции.

. Записываем уравнения граничных прямых и строим их на плоскости в прямоугольной декартовой системе координат (рисунок 1.2.3):

.

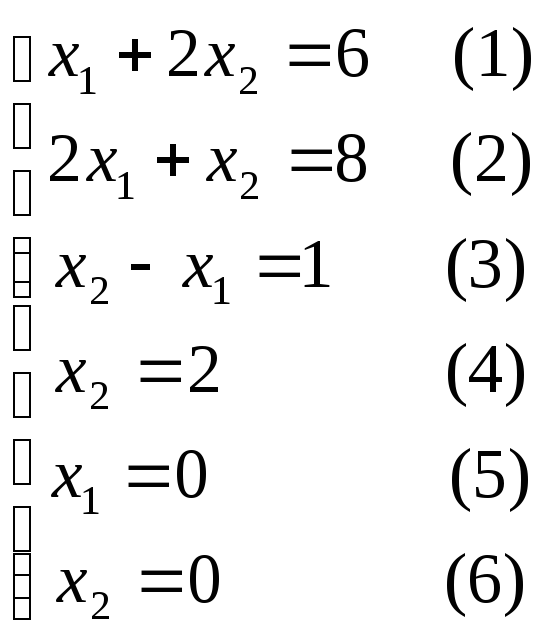Находим решение каждого неравенства и область допустимых решений (подробное описание этого пункта было рассмотрено в примере 1.2.1).

Получим пространство решений - многоугольник решений ABCDEF (показан на рисунке 1.2.3).

. Строим вектор-градиент целевой функции по двум точкам и , то есть .

. Проводим линию уровня - любой перпендикуляр к вектору-градиенту (на рисунке 1.2.3 линия уровня отмечена пунктирной линией).

 

М

Рисунок 1.2.3

. Так как задача решается на , линию уровня перемещаем в направлении вектора-градиента до тех пор, пока не достигнем последней точки выхода из области допустимых решений ABCDEF. Это и будет точка целевой функции - точка .

. Для нахождения координат точки решим систему двух уравнений граничных прямых, пересекающихся в этой точке, то есть уравнений прямых (1) и (2):

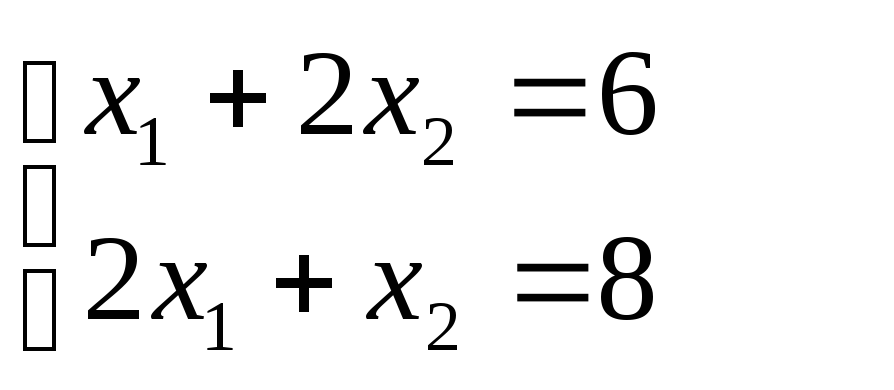, , , то есть .

. Находим значение целевой функции в точке : .

. Проведем экономический анализ рассмотренной за­дачи. Подставив координаты оптимального решения в каждое неравенство системы ограничений

,

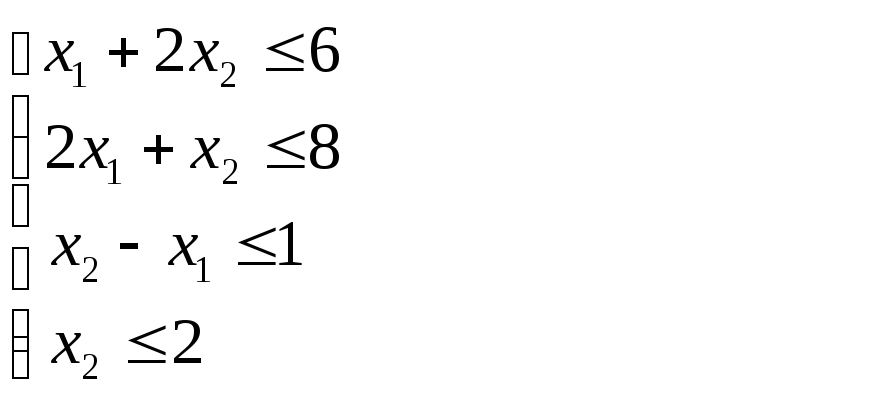видим, что первое и второе неравенства обращаются в уравнения, а третье и четвертое – в строгое неравенство:

.Это означает, что все сырье используется полностью, то есть является дефицитным ресурсом, спрос на краску К₁ превысит спрос на краску К₂ не более чем на 2т и максимальная величина спроса на краску составляет т.

Таким образом, фабрика должна производить т краски вида К₁, т краски вида К₂, при этом максимальный доход от реализации краски составляет тыс. долл.

Проведем анализ модели задачи на чувствительность.

Решим первую задачу анализа модели на чувствительность. Выясним на сколько можно сократить или увеличить запасы ресурсов вида А и В. Особенно важно проанализировать следующие два аспекта: на сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции и на сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции.

Активными ограничениями являются первое и второе, которые лимитируют запасы сырья вида А и В, следовательно, сырье вида А и В являются дефицитными ресурсами.

Рассмотрим сначала сырье А. Из рисунка 1.2.3 видно, что при увеличении запаса этого ресурса прямая (1) (или отрезок CD) перемещается вверх параллельно самой себе, постепенно "стягивая" в точку треугольник CDK. Стороны СК и DK этого треугольника представляют собой продолжения прямых, соответствующих ограничениям (2) и (4). В точке К ограничения (2) и (4) становятся активными, оптимальному решению при этом будет соответствовать точка К, а пространством (допустимых) решений становится многоугольник ABKEF. В точке К ограничение (1) (для сырья А) становится избыточным, так как любой дальнейший рост запаса соответствующего сырья не влияет ни на пространство решений, ни на оптимальное решение. Таким образом, объем сырья А не следует увеличивать сверх того предела, когда соответствующее ему ограничение (1) становится избыточным, то есть прямая (1) проходит через новую оптимальную точку К. Этот предельный уровень определяется следующим образом. Сначала нужно найти координаты точки К, в которой пересекаются прямые (2) и (4):

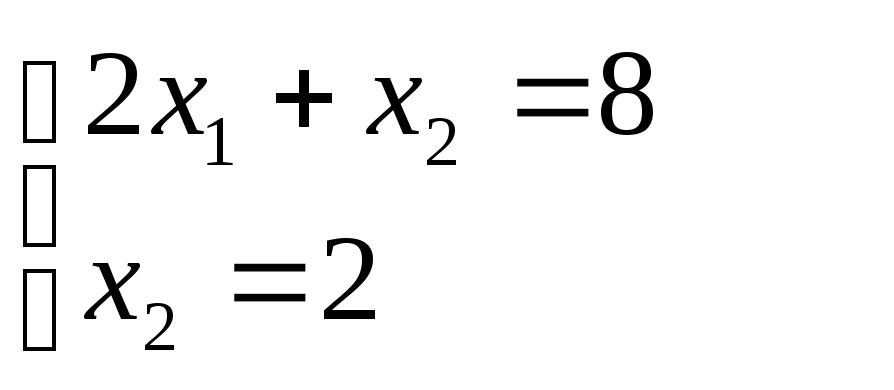, , , то есть . Подставим координаты точки К в левую часть ограничения (1) и определим максимально допустимый запас сырья А: т. Следовательно, запас сырья вида А можно увеличивать с 6 до 7 т. При этом тыс. долл.

Рассмотрим теперь вопрос о целесообразности увеличения запаса дефицитного сырья В прямая (2)). Из рисунка 1.2.3 видно, что при увеличении запаса этого сырья (прямая (2) или отрезок C В) перемещается вправо параллельно самой себе, постепенно "стягивая" в точку треугольник .

Стороны и этого треугольника представляют собой продолжения прямых, соответствующих ограничениям (1) и (6). В точке ограничения (1) и (6) становятся активными, оптимальному решению при этом будет соответствовать точка , а пространством (допустимых) решений становится многоугольник ADEF. В точке ограничение (2) (для сырья В) становится избыточным, и любой дальнейший рост запаса соответствующего сырья не влияет ни на пространство решений, ни на оптимальное решение. Таким образом, объем сырья В не следует увеличивать сверх того предела, когда соответствующее ему ограничение (2) становится избыточным, то есть прямая (2) проходит через новую оптимальную точку . Найдем координаты точки , в которой пересекаются прямые (1) и (6):

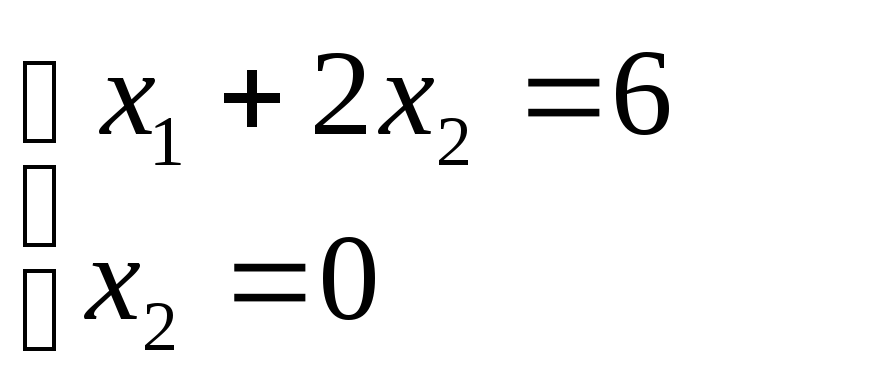, , , то есть . Подставим координаты точки в левую часть ограничения (2) и определим максимально допустимый запас сырья В: т. Следовательно, запас сырья вида В можно увеличивать с 8 до 12 т. При этом тыс. долл.

Теперь выясним, на сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?

Рассмотрим вопрос об уменьшении правой части неактивных ограничений. Рассмотрим ограничение (3)      которое представляет соотношение между спросом на краску К₁ и спросом на краску К₂. И в этом случае правую часть ограничения можно уменьшать до тех пор, пока прямая (3) (отрезок EF) не достигнет точки . При этом правая часть ограничения (3) станет равной    что позволяет записать это ограничение в виде    или в эквивалентной форме:  . Этот результат показывает, что ранее полученное оптимальное решение не изменится, если спрос на краску К₁ превысит спрос на краску К₂ не более чем на 2т.

Ограничение (4) , фиксирует предельный уровень спроса на краску К₂. Из рисунка 1.2.3 следует, что, не изменяя оптимального решения, прямую (4) (отрезок ED) можно опускать вниз до пересечения с оптимальной точкой . Уменьшение спроса, на краску К₂ до величины     никак не повлияет на оптимальность ранее полученного решения.

Результаты проведенного анализа можно свести в следующую таблицу.

№ ограничения	Тип ресурса	Максимальное изменение запаса ресурса, т	Максимальное изменение дохода от реализации краски (), тыс. долл.
1 ограничение по сырью вида А	Дефицитный	7 – 6 = +1
2 ограничение по сырью вида В	Дефицитный	12 – 8 = +4
3 ограничение - соотношение между спросом на краску К1 и спросом на краску К2	Недефицитный	- 2 – 1 = -3
4 ограничение - предельный уровень спроса на краску К2	Недефицитный

Рассмотрим вторую задачу анализа модели на чувствительность - увеличение объема какого из ресурсов наиболее выгодно. Для этого введем характеристику ценности каждой дополнительной единицы дефицитного ресурса, которую выразим через соответствующее приращение оптимального значения целевой функции. Такую характеристику для рассматриваемого примера можно получить непосредственно из таблицы, в которой приведены результаты решения первой задачи анализа на чувствительность.

Обозначим ценность дополнительной единицы ресурса через . Величина , определяется из соотношения: Воспользовавшись данными предыдущей таблицы, для ограничения (1) (сырье вида А) получим 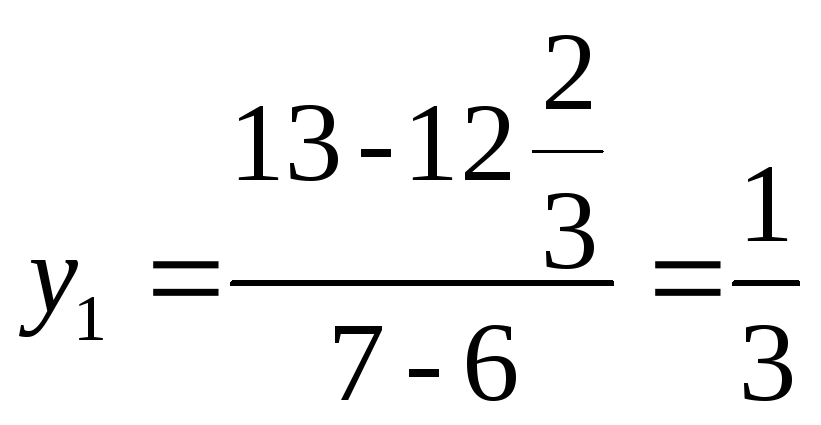, тыс. долл. ценность 1 т сырья вида А. Аналогичным образом можно определить ценность единицы каждого из остальных ресурсов 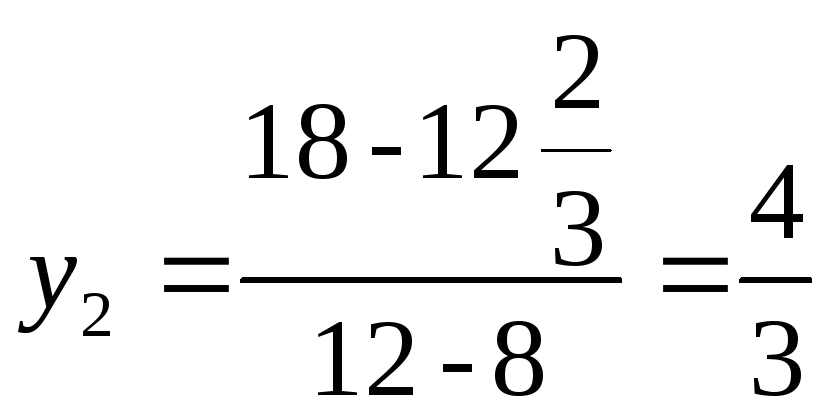, , 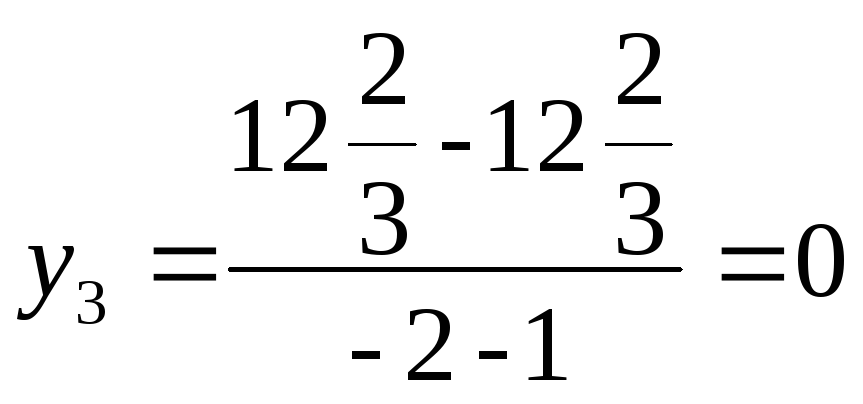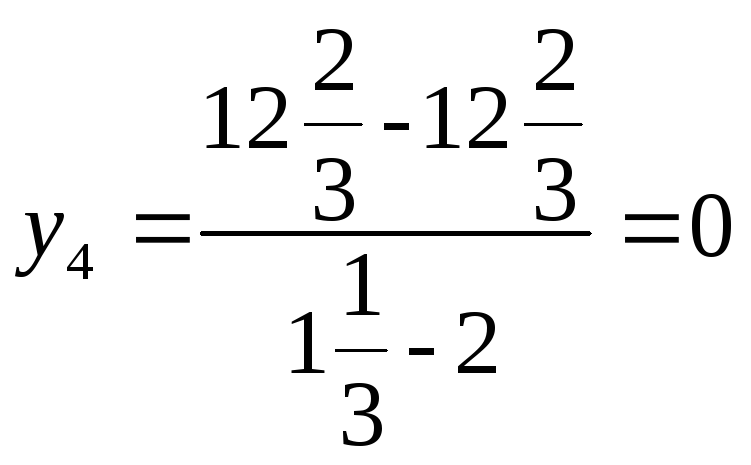и представить результаты в следующей таблице:

Ресурс	Тип ресурса	Значение , тыс. долл. за тонну
1	Дефицитный
2	Дефицитный
3	Недефицитный
4	Недефицитный

Полученные результаты свидетельствуют о том, что дополнительные вложения в первую очередь следует направить на увеличение ресурса 2 ( сырье вида В) и лишь затем - на увеличение ресурса 1 (сырье вида А). Что касается недефицитных ресурсов, то, как и следовало ожидать, их объем увеличивать не следует (,).

Рассмотрим третью задачу анализа модели на чувствительность. В каких пределах допустимо изменение коэффициентов целевой функции?

В рамках анализа модели задачи на чувствительность к изменениям коэффициентов целевой функции могут исследоваться следующие вопросы:

1) каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?

2) насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?

Рассматривая первый вопрос, обозначим через и доходы фабрики от продажи 1 т краски К₁ и 1 т краски К₂ соответственно. Тогда целевую функцию можно представить в следующем виде: .

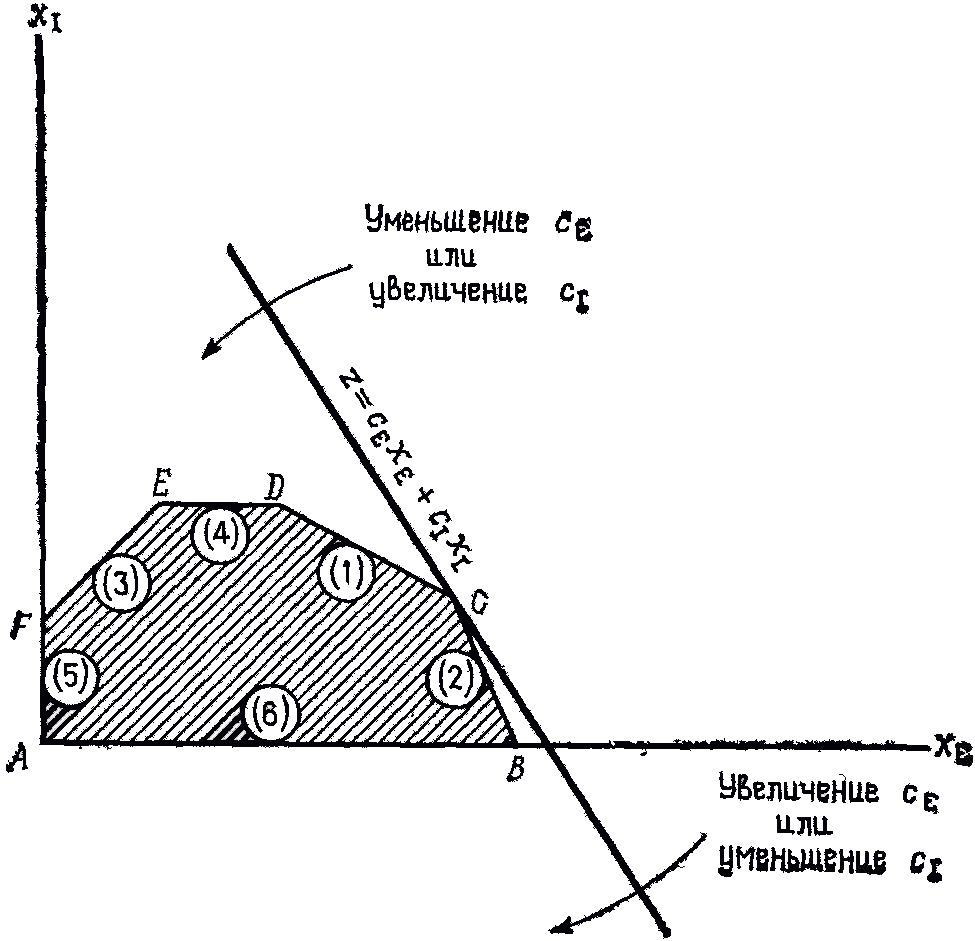
Переместим линию уровня вправо параллельно самой себе до совмещения с точкой максимума С. При увеличении или уменьшении линия уровня вращается (вокруг точки С) по часовой стрелке. Если же уменьшается или увеличивается, эта прямая вращается в противоположном направлении - против часовой стрелки. Таким образом, точка С будет оставаться оптимальной точкой до тех пор, пока наклон прямой не выйдет за пределы, определяемые наклонами прямых, соответствующих ограничениям (1) и (2). Когда наклон линии уровня станет равным наклону прямой (1), получим две альтернативные оптимальные угловые точки С и D. Аналогично, если наклон линии уровня станет равным наклону прямой (2), будем иметь альтернативные оптимальные угловые точки В и С. (Наличие альтернативных оптимумов свидетельствует о том, что одно и то же оптимальное значение может достигаться при различных значениях переменных. Как только наклон линии уровня выйдет за пределы указанного выше интервала, получим некоторое новое оптимальное решение (точка В или точка D).

Найдем допустимый интервал изменения , при котором точка С остается оптимальной. Исходное значение коэффициента = 2 оставим неизменным, а значение можно увеличивать до тех пор, пока линия уровня не совпадет с прямой (2), или уменьшать, пока линия уровня не совпадет с прямой (1). Эти крайние значения коэффициента можно определить из равенства наклонов линии уровня и прямой (2) (максимальное значение линии уровня) и равенства наклонов линии уровня и прямой (1) (минимальное значение ). Найдем угловой коэффициент линии уровня: , угловой коэффициент граничной прямой (1): , и угловой коэффициент граничной прямой (2): . Из равенства , или находим минимальное значение , а из равенства , или - максимальное значение . Таким образом, , , то есть оптимальное решение задачи не изменится, ес­ли оптовая цена краски К₁ будет находиться в диапа­зоне от 1 до 4 тыс. долл., при этом доход фабрики будет заключен в пределах от 6 до 16, тыс. долл. (,).

Аналогично находится диапазон изменения коэффициента если будет неизменным: - угловой коэффициент линии уровня. Из равенства , или находим максимальное минимальное значение , а из равенства , или - минимальное значение . Таким образом, , , то есть оптимальное решение задачи не изменится, ес­ли оптовая цена краски К₂ будет находиться в диапа­зоне от 1,5 до 6 тыс. долл., при этом доход фабрики будет заключен в пределах от 12 до 18, тыс. долл. (,).

Таким образом, из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс. руб./т (), то наиболее выгодным будет производство красок в точке D (см. рисунок). При этом общее потребление сырья В снизится, что приведет к его недефицитности (прямая (2)), а дефицитными будут ресурсы (1) и (4).