
LAB3bak
.pdf
4. Модуль Graph. Графический режим
Графический режим ПК существенно отличается от текстового как по принципам функционирования, так и по возможностям. Графика применяется практически во всех серьезных программных разработках, так как позволяет увидеть результаты расчетов в виде чертежей, графиков, иллюстраций в движении. Фирмой Borland разработана библиотека графических функций (Модуль Graph.tpu) как приложение к Turbo-пакетам фирмы Borland и графические драйверы - файлы *.bgi (Borland Graphics Interface ), обеспечивающие взаимодействие программ с графическими устройствами.
1. Подключение графической библиотеки производится оператором:
Uses Graph;
2. Переключение из текстового режима в графический (инициализация) осуществля-
ется процедурой:
Procedure InitGraph(Gd, Gm, 'way');
где Gd - имя графического драйвера (параметр-переменная),
Gm - номер графического режима монитора (параметр-переменная),
'way' - путь к файлам с графическими драйверами (*. bgi), например, C:\TP\BGI. Первые два параметра должны иметь целый тип, третий параметр строковый.
В графическом режиме изображение формируется из точек (пикселов) разных цветов. Количество точек на экране и число допустимых цветов можно задавать выбором подключаемого драйвера и номером графического режима. Вариации графических режимов весьма разнообразны, особенно для качественных мониторов. Например, адаптер IBM 8514 / A может обеспечить разрешение 1024 х768 точек и 256 цветов.
Приведем таблицу графических возможностей для мониторов EGA, VGA.
Монитор |
драйвер |
режим |
Число точек |
Число |
Число видео- |
|
|
"Gd" |
"Gm" |
на экране |
цветов |
страниц |
|
EGA |
EGA |
0 |
640 |
x 200 |
16 |
4 |
VGA |
EGA |
1 |
640 |
x 350 |
16 |
2 |
VGA |
0 |
640 |
x 200 |
16 |
4 |
|
|
VGA |
1 |
640 |
x 350 |
16 |
2 |
|
VGA |
2 |
640 |
x 480 |
16 |
1 |
Обычно драйверы подключаются в режиме автоопределения используемого монитора ПК. Для этого перед инициализацией графического режима задается Gd:= Detect; или Gd:= 0;. В этом случае по умолчанию устанавливается режим с наибольшим числом точек на экране, а значение параметра "Gm" игнорируется. Номер наибольшего режима для текущего драйвера возвращает функция Function GetMaxMode:Integer;.
Разрешающую способность для текущего графического режима можно определить функ-
циями, возвращающими максимальные значения координат экрана:
Х |
Function GetMaxX: Integer; - по |
|
оси "Х"; |
|
Function GetMaxY: Integer; - по |
Y |
оси "Y". |
|
Начало координат (X= 0, Y= 0) расположено в левом верхнем углу эк- |
рана. Ось Х направлена слева направо, ось Y - сверху вниз (Рис.).
3. Для возврата из графического режима в текстовый можно использовать процедуру
Procedure CloseGraph.
Простейшие графические процедуры и функции
После инициализации графического режима экран очищается и можно использовать процедуры рисования.
Procedure SetBkColor(N: Word); - установить цвет "N" для пикселов фона (по умолчанию установлен черный цвет фона).
Procedure SetColor(N: Word); - установить цвет "N" для выводимых линий (По умолчанию установлен белый цвет).
Procedure PutPixel(X, Y: Integer, N: Word); - высветить цветом "N" пиксел с коорди-
натами X, Y.
Function GetMaxColor: Integer; - функция возвращает максимальный номер цвета палитры (цвет задается аналогично цветам текста в модуле Crt).
Procedure Circle(X, Y:Integer, R:Word); - строит текущим цветом окружность с цен-
тром X, Y и радиусом R.
Procedure Line(x1, y1, x2, y2: Integer); - строит текущим цветом отрезок прямой линии от точки с координатами x1, y1 к точке с координатами x2, y2.
Procedure Rectangle(x1, y1, x2, y2: Integer); - строит текущим цветом прямо-
угольник с левым верхним углом в точке с координатами x1, y1 и правым нижним углом в точке с координатами x2, y2.
Function GetPixel(X, Y: Integer): Word; - функция возвращает цвет пиксела с координатами X, Y.
Procedure ClearDevice; - очищает графический экран, закрашивает его цветом фона устанавливает указатель текущей позиции в точку с координатами (0, 0)
Пример 1. |
|
|
Uses Crt, Graph; |
|
|
var |
{ раздел описаний} |
|
ch: char; |
|
|
Gd, Gm, Gx, Gy, xc, yc: integer; |
|
|
Begin |
|
|
Gd:=Detect; |
|
|
InitGraph(Gd,Gm,'C:\tp\bgi'); |
(* инициализация графики *) |
|
Randomize; |
|
|
Gx:=GetMaxX; Gy:=GetMaxY; |
|
|
{---------------------------------------------------------- |
|
|
Фрагмент N 1 программы "небо в алмазах" |
( рисование пикселов ). |
|
--------------------------------------------------------------SetColor(0); |
|
} |
|
|
|
Repeat |
|
|
i:= 9 + random(7); |
|
|
xc:= random(Gx); |
|
|
yc:= random(Gy); |
|
|
PutPixel(xc, yc, i); |
|
|
Circle(xc, yc, 3) |
|
|
Until KeyPressed; |
|
|
{---------------------------------------------------- |
|
} |
While KeyPressed do ch:= ReadKey; |
|
{ очистка буфера клавиатуры } |
CloseGraph; |
|
{ закончить работу в графическом режиме } |
End. |
|
|
После инициализации графики определяются переменные Gx, Gy - максимальные значе-
ния координат по осям X, Y. Назначается черный цвет для линий, которые будут выводиться. Затем в цикле повторяется до нажатия любой клавиши высвечивание точек (пикселов) с номерами цвета "i" от 9 до 15 и координатами xc, yc. Значения координат точек и номеров цвета определяются из заданного диапазона функцией Random. Чтобы точки не "забивали" экран, некоторые из них "гасятся" окружностью радиусом 3 пикселя с центром в появившейся точке.
Пример 2. Построение функции Y=Abs(Sin(x)).
program Funk; |
|
uses Graph; |
(*подключение графической библибтеки*) |
var x, y,h,xk,xn:real; |
|
gd,gm:Integer; |
|
function f(x:real):real; |
(* подпрограмма-функция вычисления abs(sin(x)) *) |
begin |
|
f:=abs(sin(x)) |
|
end; |
|
Begin |
(*начало главной программы*) |
gd:=Detect; |
|
Initgraph(gd,gm,'c:\bp\bgi'); |
(*включение графического режима*) |
xn:=-10; xk:=10; |
(*начало и конец по оси абсцисс х*) |
h:= (xk-xn)/1000; |
(*величина шага приращения аргумента*) |
x:=xn; |
|
while x<xk do |
|
begin |
|
y:=f(x); |
(*вычисление функции в точке*) |
putpixel(round(x*30+300),round(200-y*200),white); {строим точку на экране} |
|
x:=x+h |
(*переход к следующей точке*) |
end; |
|
readln |
|
end. |
|

5. Численное решение алгебраических и трансцендентных уравнений
Метод половинного деления
Блок-схема алгоритма метода половинного деления представлена на рис. 1. Он состоит из следующих операций. Сначала вычисляются значения функций в точках, расположенных через равные интервалы на оси х. Это делается до тех пор, пока не
Рис. 1 Блок-схема алгоритма половинного деле-
ния
будут найдены два последовательных значения функции f(хп) и f(xn+1), имеющие противоположные знаки. (Напомним, если функция непрерывна, изменение знака указывает на существование корня.)
Затем по формуле
вычисляется среднее значение х в интервале значений [xn, хп+1] и находится значение функции f(хср). Если знак f(хср) совпадает со знаком f(хп), то в дальнейшем вместо f(хп) используется f(хср). Если же f(хср) имеет знак, противоположный знаку f(xn), т. е. ее знак совпадает со знаком f(хп+1), то на f(xср) заменяется это значение функции. В результате интервал, в котором заключено значение корня, сужается. Если f(хср) достаточно близко к нулю, процесс заканчивается , в противном случае он продолжается. На рис. 2 эта процедура показана графически. Хотя метод половинного деления не обладает высокой вычислительной эффективностью, с увели-
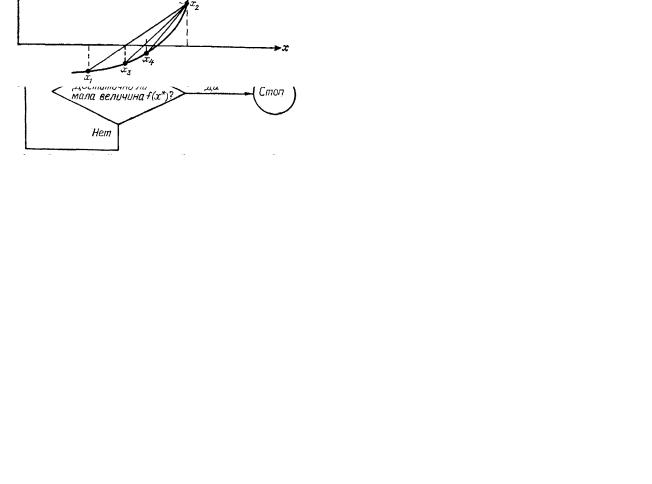
чением числа итераций он обеспечивает получение все более точного приближенного значения корня. После того как впервые найден интервал, в котором заключен корень, его ширина после N итераций убывает в 2N раза.
Метод хорд.
В основе этого метода лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки. При отыскании корня этот метод нередко обеспечивает более быструю сходимость, чем предыдущий. Блок-схема алгоритма метода хорд дана на рис. 3. Счет ведется следующим образом. Сначала определяются значения функции в точках, расположенных на оси х через равные интервалы. Это делается до тех пор, пока не будет найдена пара последовательных значений функции f(хп) и f(хп+1), имеющих противоположные знаки. Прямая, проведенная через эти две точки, пересекает ось х при значении
Рис. 3. Блок-схема алгоритма метода хорд.
Метод Ньютона
Это значение аргумента используется для определения значения функции f(x*), которое сравнивается со
значениями функций f(xn) и f(xn+l) и в дальнейшем используется вместо то-
го из них, с которым оно совпадает по знаку. Если значение f(x*) недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет достигнута необходимая степень сходимости. На рис. 4 процесс решения показан графически.
Рис. 4 Метод хорд.
Метод последовательных приближений, разработанный Ньютоном, очень широко используется при построении итерационных алгоритмов. Его популярность обусловлена тем, что в отличие от двух предыдущих методов для определения интервала, в котором заключен корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции в методе Ньютона осуществляется экстраполяция с помощью касательной к кривой в данной точке. На рис. 5 показана блок-схема алгоритма этого метода, в основе которого лежит разложение функции f(x) в ряд Тейлора

f (xn + h) = f (xn ) + hf '(xn ) + h2 f (xn )+....
2
Члены, содержащие h во второй и более высоких степенях, отбрасываются; используется соотношение xn+h=xn+1. Предполагается, что переход от хn к xn+1 приближает значение функции к нулю так, что f(xn+h)=0. Тогда
xn+1=xn-f(xn)/f’(xn)
Значение xn+1 соответствует точке, в которой касательная к кривой в точке хп пересекает ось х. Так как кривая f(x) отлична от прямой, то значение функции f(xn+1)
Рис. 5 Блок-схема алгоритма Ньютона.
скорее всего не будет в точности равно нулю. Поэтому вся процедура повторяется, причем вместо хп используется хп+1. Счет прекращается по достижении достаточно малого значения f(xn+l). На рис. 6 процесс решения уравнения методом Ньютона показан графически. Совершенно ясно, что быстрота сходимости в большой мере зависит от удачного выбора исходной точки. Если в процессе итераций тангенс угла наклона
Рис. 6 Метод Ньютона
касательной f' (х) обращается в нуль, то применение метода осложняется. Можно также показать, что в случае бесконечно большого f"(x) метод также не будет достаточно эффективным. Так как условие кратности корней имеет вид f(x) = f' (х)= 0, то в

этом случае метод Ньютона не обеспечивает сходимость. Отметим, что иногда используется другой способ контроля сходимости, состоящий в сравнении хп и xn+l.
Метод секущих
Один из недостатков метода Ньютона состоит в том, что, пользуясь им, приходится дифференцировать функцию f(x). Если нахождение производной затруднено, то можно воспользоваться некоторым приближением, которое и составляет основу метода секущих. Заменив производную f'(x), используемую в методе Ньютона
xn+1 = xn − f (xn ) , f '(xn )
разностью последовательных значений функции, отнесенной к разности значений аргумента
F‘(xn)= f (xn ) − f (xn−1 ) , xn − xn−1
получим следующую итерационную формулу:
xn+1 = xn − f (xn ) f '(xn )
Схема алгоритма для этого метода та же, что и для метода Ньютона (несколько иной вид имеет итерационная формула). В сущности в методе секущих для отыскания корня используется комбинация интерполяции и экстраполяции. В своей интерполяционной части этот метод эквивалентен методу ложного положения. Как и в случае метода Ньютона, счет заканчивается, когда последовательные значения х совпадают с некоторой приемлемой точностью или когда значение функции f(x) становится достаточно близким к нулю. В случае кратных корней при использовании метода секущих возникают те же трудности, что и при использовании метода Ньютона.
Метод простой итерации
Для применения этого метода уравнение f(x) =0 обязательно приводится к следующему виду:
x = g(x).
Практически к такому виду можно привести любое уравнение. Тогда, соответствующая итерационная формула имеет вид
xп+1 = g(xn).
Блок-схема алгоритма метода представлена на рис. 7. Простота метода простой итерации делает его привлекательным, однако не следует забывать, что и этому методу присущи недостатки, так как он не всегда обеспечивает сходимость. Поэтому для любой программы, в которой используется этот алгоритм, необходимо предусматривать контроль сходимости и прекращать счет, если сходимость не обеспечивается.
Рис. 7 Блок-схема метода простой итерации.
Пример решения уравнения
Предстоит решить уравнение x-tgx=0
воспользовавшись рассмотренными выше методами.
1. Перед решением необходимо:
Определить интервалы, в которых находятся корни уравнения. Это необхо-
димо сделать, чтобы выбрать начальное значение х. Здесь можно, например, изобразить график зависимости tgx и х, из которого следует, что значение первого ненулевого корня уравнения заключено между 3 и 2. Поэтому примем значение х=4.5.
2. Уточнить значение корня, решением уравнения используя рассмотренные методы (Внимание! Используемые методы сами не находят корни уравнения, а лишь уточняют их значение.). Поэтому, очень важен пункт 1, в котором определяют интервалы нахождения корня. Если интервал определен неверно (т.е. там корня нет корня), то программа обычно зацикливается:
а) Метод половинного деления
program urdel2;
(*Программа решения трансцендентного уравнения*)
(* |
|
F(X)=X-TAN(X)=0 |
*) |
|
(* |
методом половинного деления |
*) |
||
(* Счет прекращается при F=e менее 0.00001 |
*) |
|||
var |
|
|
|
|
|
i:integer; |
|
|
|
|
xh,xk,xcp,xn,xn1,fxn,fxcp,x,e:real; |
|
||
function F(x:real):real; |
|
|
||
begin |
|
|
|
|
|
f:=x-sin(X)/COS(x) |
|
|
|
end; |
|
|
|
|
begin |
|
|
|
|
e:=0.0001; {задание точности} |
|
|||
xh:=2; |
{начальное и } |
|
||
xk:=5.5; |
{конечное значение интервала } |
|
||
writeln('------------------'); |
|
|
||
writeln('iteration number'); |
|
|||
writeln('------------------'); |
|
|
||
xn:=xh; |
|
|
|
|
xn1:=xk; |
|
|
|
|
i:=0; |
{кол-во иттераций вычисления интервалов} |
|||
|
repeat |
|
|
|
|
xcp:=(xn+xn1)/2; |
(*определение середины*) |
||
|
fxn:=f(xn); |
(*определение функции в начале*) |
||
|
fxcp:=f(xcp); |
(*и в середине промежутка*) |
||
|
if (fxn*fxcp)>0 then xn:=xcp (*знаки в середине и начале*) |
|||
|
else xn1:=xcp; |
(*совпадают*) |
|
|
|
i:=i+1; |
|
|
|
|
writeln(i:2,' ',xn:6:5); |
(*вывод очередной иттерации*) |
||
|
until abs(fxn)<=e; |
(*прверка заданной точности*) |
||
write('=================');
end.
б) Метод хорд.
program urdel2;
(*Программа решения трансцендентного уравнения*)
(* |
F(X)=X-TAN(X)=0 |
*) |
|
(* |
методом Хорд |
*) |
|
(* Счет прекращается при F=e менее 0.00001 |
*) |
||
var |
|
|
|
|
i:integer; |
|
|
|
xh,xk,xcp,xn,xn1,fxn,fxcp,x,e:real; |
|
|
function F(x:real):real; |
|
||
|
begin |
|
|
|
f:=x-sin(X)/COS(x) |
|
|
|
end; |
|
|
begin |
|
|
|
e:=0.0001; |
|
|
|
xh:=2; |
|
|
|
xk:=5.5; |
|
|
|
writeln('------------------ |
'); |
|
|
writeln('iteration |
number'); |
|
|
writeln('------------------ |
'); |
|
|
xn:=xh; xn1:=xk; |
|
|
|
i:=0; repeat
xcp:=xn-f(xn)*((xn1-xn)/(f(xn1)-f(xn))); fxn:=f(xn);
fxcp:=f(xcp);
if (fxn*fxcp)>0 then xn1:=xcp
else xn:=xcp; |
|
i:=i+1;x:=f(xn); |
|
writeln(i:2,' ',xn:6:5,x); |
|
until abs(f(xn))<=e; |
{проверка заданной точности, при которой заканчива- |
ется вычисление} write('=================');
end.
в) Метод Ньютона
program urnewton;
(*Программа решения трансцендентного уравнения*) (* F(X)=X-TAN(X)=0 *)
(*Методом Ньютона. Счет прекращается при F=e менее 0.00001*)
var
i:integer;
f,df,x,e:real; |
|
|
|
begin |
|
|
|
e:=0.0001; |
(*указанная точность*) |
||
x:=4.5; |
(*начальное значение*) |
||
writeln('------------------'); |
|
|
|
writeln('iteration number'); |
(* шапка таблицы*) |
||
writeln('------------------'); |
|
|
|
i:=0; |
(*обнуление счетчика циклов*) |
||
repeat |
|
|
|
f:=x-sin(X)/COS(x); |
|
(* вычисление функции *) |
|
df:=1.0-1./(cos(x)*cos(x)); |
(* |
производной*) |
|
x:=x-F/df; i:=i+1; |
(* |
|
аргумента*) |
writeln(i:2,' ',x:6:5) |
(*вывод значений в таблицу*) |
||
until abs(f)<=e; |
(*проверка точности*) |
||
write('=================');
end.
Таким образом, метод Ньютона обеспечивает очень быструю сходимость при начальном значении х=4.5 (это можно определить по количеству выполненных иттераций). Отметим, что при начальных значениях х=4.0 или 5.0 сходимость уже не достигается.
г) Метод простой итерации (самый простой и часто используемый способ). Применить указанный метод к нахождению корней уравнения х2=sin(x).
program iter;
(*решение уравнения x2=sin(x)*) (*методом простых итераций*)
var
i:integer;
y,xm,f,df,x,e:real; begin e:=0.0000000001; y:=5.45; writeln('------------------');
writeln('iteration number'); writeln('------------------');
i:=0;x:=0;
while abs(x-y)>e do begin
x:=y;
y:=sqrt(abs(sin(x)));
