Лабораторная работа №3

Решение логических задач школьного курса повышенной сложности

Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Алгебра логики возникла в середине 19 века в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С. Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.) и дальнейшим развитием математической логики (последняя четверть 19 в. — 1-я половина 20 в.), предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием понимается каждое предложение, относительно которого имеет смысл утверждать, истинно оно или ложно. Примеры высказываний: «кит — животное», «все углы — прямые» и т.п. Первое из этих высказываний является, очевидно, истинным, а второе — ложным. Употребляемые в обычной речи логические связки «и», «или», «если..., то...», «эквивалентно», частица «не» и т. д. позволяют из уже заданных высказываний строить новые, более «сложные» высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.

В отличие от обычной алгебры, изучающей математические функции, алгебра логики изучает логические функции. Известно, что функция — это закон соответствия между переменными. Следовательно, логическая функция— это закон соответствия между логическими переменными.Логическая переменная— это такая переменная, которая может принимать одно из двух возможных значений: 0 («ложь») и 1 («истина»).

Логическим выражением называется выражение, о котором можно сказать истинно оно или ложно.

Примеры:

«5>8» - логическое выражение, т.к. о нем можно сказать, что оно ложно.

«Эту девочку зовут Юля» - логическое выражение.

«Подайте книгу» - это не логическое выражение, т.к. о нем нельзя сказать, истинно оно или ложно

Логическая функция может также принимать два значения.

Таким образом, логические переменные и функции определены на множестве двух значений — {0,1}.

ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое — единицей. На такие компоненты воздействуют двоичные сигналы. Под воздействием сигналов компоненты изменяют свои состояния, т. е. состояние компонентов или значения их выходных сигналов зависят от значений воздействующих сигналов. Очевидно, что функционирование компонентов ЭВМ следует описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.

Логические функции характеризуются (задаются) так называемыми таблицами истинности, или соответствия. Таблица истинности— это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.

Основные логические функции

Функция отрицания

Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот. Запись этой функции:

F=.

Конъюнкция может быть обозначена следующими символами:

¬,¯, не, not.

Черта над переменной xявляется признаком отрицания (инверсии). Таблица истинности этой функции представлена на рис. 1а. Функция логического отрицания описывает функционирование логического элемента НЕ (рис. 1б).

Условно-графическое обозначение элемента НЕ приведено на рис. 1в. Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (x=0,F=1) и, наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x=1,F=0). Графически отрицание можно представить с помощью кругов Эйлера (рис. 2).

а) б) в)

x	F
0	1
1	0

Рис. 1. Элемент НЕ

Рис. 2. Графическое представление отрицания на множестве

Функция логического умножения (конъюнкция)

Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Эта функция называется также конъюнкцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты записи конъюнкции:

F=;F=•;F=;F=&.

Конъюнкция может быть обозначена следующими символами:

, &, •, ∩, and, и.

Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а. Из рассмотрения таблицы следует, что эта функция принимает единичное значение на наборе 4. Логическое умножение описывает работу элемента И (рис. 3б). Графически конъюнкцию можно представить с помощью кругов Эйлера (рис. 4).

а) б) в)

		F
0	0	0
0	1	0
1	0	0
1	1	1

Рис. 3. Элемент И

Рис. 4. Графическое представление конъюнкции на множествах

Конъюнкция на числовых множествах (операция пересечения): {a,b,c} {b,c,d,e}={b,c}.

Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе 1, и на входе 2.

В общем случае элемент И может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.:

F=•••…•.

Функция логического сложения (дизъюнкция)

Логическое сложение – это логическая функция, по крайней мере, от двух переменных, которая принимает нулевое значение при нулевых значениях всех переменных. Эта функция называется также дизъюнкцией. Таблица истинности элементарной дизъюнкции представлена на рис. 3а. Элементарная дизъюнкция принимает единичное значение на наборах 1, 2, 3 и нулевое значение – только на наборе 0. Функция записывается в одном из двух видов: F=илиF=+.

Знак «плюс» не является алгебраическим, т.к. при =1, =1 дизъюнкцияF=+=1

Дизъюнкция может быть обозначена следующими символами:

, +,, or, или.

Дизъюнкция описывает функционирование элемента ИЛИ (рис. 5б). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или на входе 2, или на двух входах единичные сигналы. И только в том случае, когда на оба входа поступают нулевые сигналы, на выходе элементов появляется нулевой сигнал.

В общем случае элемент ИЛИ может иметь n входов (рис. 5в). При этом он реализует дизъюнкцию от n переменных.

а) б) в)

		F
0	0	0
0	1	1
1	0	1
1	1	1

Рис. 5. Элемент ИЛИ

Рис. 6. Графическое представление дизъюнкции на множествах

Дизъюнкция на числовых множествах (операция объединения): {a,b,c}{b,c,d,e}={a,b,c,d,e}.

Равнозначность (эквиваленция)

Равнозначность – это логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных. Одинаковые по значению переменные называются равнозначными, поэтому функция носит название «равнозначность».

Запись функции:

F=+.

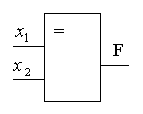
Таблица истинности функции равнозначности представлена на рис. 7а. Эта функция реализуется элементом равнозначности (сравнения), который показан на рис. 7б.

Эквиваленция может быть обозначена следующими символами:

~, ,,.

Элемент используется для сравнения двоичных сигналов.

		F
0	0	1
0	1	0
1	0	0
1	1	1

а) б)

Рис. 7. Элемент равнозначности

Логическое следование (импликация)

Обозначение логического следования: F=→.

Высказывание F=→будем считать истинным во всех случаях, кроме случая, когдаистинно, аложно. Таблица истинности представлена на рис. 8.

		F=→
0	0	1
0	1	0
1	0	0
1	1	1

Рис. 8. Элемент импликации

Импликация может быть обозначена следующими символами:→, ,.

Элемент (штрих) Шеффера

Обозначение:

;.

Другое название этой функции: «И-НЕ».

Высказывание будем считать ложным, когдаиравны единице. Таблица истинности представлена на рис. 9.

		
0	0	1
0	1	1
1	0	1
1	1	0

Рис. 9. Элемент (штрих) Шеффера

Элемент Вебба (стрелка Пирса)

Обозначение:

;.

Высказывание будем считать истинным только тогда, когда оба операндаиравны нулю. Таблица истинности представлена на рис.10.

Другое название этой функции: «ИЛИ-НЕ».

0	0	1
0	1	0
1	0	0
1	1	0

Рис. 10. Элемент Вебба (стрелка Пирса)

Сложение по модулю 2.

Обозначение:

;;XOR .

Высказывание будем считать истинным, если первый операндне равен второму операнду. Таблица истинности представлена на рис. 11.

Другие названия этой функции: «исключающее ИЛИ», «логическое ЛИБО», «неравносильность», «неэквивалентность», «логическое сложение», «булево сложение».

0	0	0
0	1	1
1	0	1
1	1	0

Рис. 11. Сложение по модулю 2

Коимпликация

Обозначение:

;.

Высказывание будем считать истинным, если первый операндравен 1, а второй операнд равен 0. Таблица истинности представлена на рис. 12.

0	0	0
0	0	0
1	0	1
1	1	0

Рис. 12 Таблица истинности функции коимпликация

Приоритет операций в логическом выражении, не содержащем скобок:

1. Отрицание.

2. Конъюнкция, *, /, div,mod.

3. Дизъюнкция, +, -.

4. Операция отношения.

Для усиления операции используются скобки.