

Предел суммы, произведения и частного
Переход к пределу в неравенствах, предел промежуточной функции
Теорема (о переходе к пределу в неравенствах): Пусть существуют конечные пределы в
некоторой окрестности т. x0 |
lim f x A , |
lim g x B . Тогда: если |
f x g x , то |
|
x x0 |
x x0 |
|
A B . |
|
|
|
Доказательство. f x A x , g x B x , тогда: A x B x , A B x
Теорема (о пределе промежуточной функции): Если |
f x g x h x в |
|||
некоторой окрестности т. x0 |
и lim f x lim h x A , то |
lim g x A . |
||
|
x x0 |
x x0 |
|
x x0 |
Доказательство. Пусть lim g x B , тогда по теореме о переходе к пределу в |
|||
x x0 |
|
|
|
неравенствах: lim f x lim g x , A B , |
lim g x lim h x , B A , |
||
x x0 |
x x0 |
x x0 |
x x0 |
Следовательно, A B и |
lim g x A . |
|
|
|
x x0 |
|
|

Непрерывность функции в точке |
|
|
|
|
, если lim f x f x0 . |
|
|
|
|||||||||||||||||
Функция f x называется непрерывной в т. |
x0 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
Замечание: элементарные функции непрерывны в точках, где определены. |
|
|
|
|
|
||||||||||||||||||||
Теорема (о переходе к пределу, под знаком непрерывности): Если функция |
f x |
|
|||||||||||||||||||||||
непрерывна в т. |
x0 , то lim f x f |
|
lim x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x x0 |
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Доказательство. Т.к. lim x x0 |
и функция непрерывна, т.е. lim f x f x0 . |
||||||||||||||||||||||||
|
|
x x0 |
|
|
|
lim x . |
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
||||||
Следовательно lim f x f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x x0 |
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Непрерывность основных элементарных функций |
f x непрерывна в т. x0 , а |
||||||||||||||||||||||||
Теорема (о непрерывности сложной функции): Пусть |
|||||||||||||||||||||||||
функция x t непрерывна в т. t0 . Тогда сложная функция |
f t непрерывна |
||||||||||||||||||||||||
в точке t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
lim f |
t |
|
|
lim f |
x f |
x |
f |
lim t |
f |
|
t |
|
|
|
||||||||||
|
t t0 |
|
|
|
|
x x0 |
|
|
|
|
0 |
|
t |
t0 |
|
|
|
0 |
|
||||||
Теорема: Пусть |
f x |
и g x |
непрерывны в т. |
x0 , тогда |
f x0 g x0 , |
|
|
|
|||||||||||||||||
f x0 g x0 , |
f x0 |
|
|
( g x0 |
0 ) тоже непрерывны в этой точке. |
|
|
|
|
|
|||||||||||||||
g x0 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство: основано на свойствах предела. Т.к. функция непрерывна, то
A f x0 .
Теорема об асимптотическом разложении непрерывной функции
Теорема (асимптотическое разложение непрерывной функции): Если функция f x
непрерывна в т. x0 , то в некоторой окрестности этой т., функция f x представима в
виде: f x f x0 O x x0 .
Доказательство. Рассмотрим lim f x A . По теореме об асимптотическом
x x0
разложении функции имеющей предел: f x A O x x0 . Т.к. функция
непрерывна, то lim f x f x0 , т.е. A f x0 .
x x0
Свойства функций, непрерывных на отрезке
Свойства (для интервалов a;b , a;b и a;b ):
1) Если функция y f x непрерывна в точке x0 , то в некоторой окрестности этой
точки знак y f x |
совпадает со знаком f x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2) Если функция y f x |
непрерывна на интервале a;b и |
f a f b 0 , то |
||||||||||||||||||||||
существует хотя бы одна точка c a;b , т.ч. |
f c 0 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3) Если функция y f x |
непрерывна на интервале a;b , то она достигает на этом |
|||||||||||||||||||||||
интервале наибольшее и наименьшее значения, т.е. x1 a;b , т.ч. |
f x1 M и |
|||||||||||||||||||||||
x2 a;b f x2 m . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) Если функция y f x |
непрерывна на интервале a;b , то она ограничена. |
|
|
|||||||||||||||||||||
Теоремы о переходе к пределу под знаком непрерывной функции, о |
|
|
|
|
|
|||||||||||||||||||
непрерывности сложной функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
|
|||||||
Теорема (о переходе к пределу, под знаком непрерывности): Если функция |
|
|||||||||||||||||||||||
непрерывна в т. x0 , то lim f x f |
|
lim x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x x0 |
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство. Т.к. lim x x0 и функция непрерывна, т.е. lim f x f x0 . |
||||||||||||||||||||||||
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
||||
Следовательно lim f x f lim x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x x0 |
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема (о непрерывности сложной функции): Пусть |
f x непрерывна в т. x0 , а |
|||||||||||||||||||||||
функция x t непрерывна в т. t0 . Тогда сложная функция |
f t непрерывна |
|||||||||||||||||||||||
в точке t0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. lim f |
|
t |
|
lim f |
x f x f |
lim t |
f |
|
t |
|
|
|
||||||||||||
t t0 |
|
|
|
x x0 |
|
|
|
0 |
|
|
|
|
t t0 |
|
|
|
|
|
0 |
|
||||
Односторонние пределы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f x A : Число |
A называется односторонним пределом слева, если 0 , |
|||||||||||||||||||||||
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , т.ч. x x0 , |
|
f x A |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x0 x x0 : |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
lim f x B : Число B называется односторонним пределом справа, если |
|
|
|
|||||||||||||||||||||
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , 0 , т.ч. x x0 , x0 x x0 : |
|
|
f x A |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||

Теорема: Для того, чтобы f x имела в т. x0 |
предел, необходимо и достаточно чтобы |
|
существовали односторонние пределы: lim |
f x lim |
f x A . |
x x0 0 |
x x0 0 |
|
Функция f x называется непрерывной в т. |
x0 , если lim f x f x0 . |
|
|
x x0 |
|
Замечание: элементарные функции непрерывны в точках, где определены.
Точки разрыва функции, их классификация
Точка x0 |
, называется точкой разрыва первого рода если: 1) lim f x f x0 2) |
|
x x0 |
Существуют конечные односторонние пределы, но они не совпадают, т.е. не существует предела.
Точка x0 , называется точкой разрыва второго рода если хотя бы один из односторонних пределов не существует или равен бесконечности.
Замечательные пределы
Эквивалентные бесконечно малые функции
Функция x называется бесконечно малой, если |
lim x 0 , т.е. 0 , |
||||||||
|
|
|
|
|
|
|
|
|
x x0 |
0 , т.ч. x x0 , |
|
x x0 |
|
: |
|
x |
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Функции x и x называются эквивалентными б/м при x x0 , если
lim |
x |
1 и обозначаются x ~ x . |
|
x |
|||
x x0 |
|
Теорема: Для того, чтобы x ~ x , необходимо и достаточно, чтобыx x была б/м более высокого порядка чем x и x .

Таблица эквивалентных бесконечно малых
sin x ~ x , tgx ~ x , 1 cos x ~ x2 , arcsin x ~ x , arctgx ~ x , ex 1 ~ x ,
2
ln 1 x ~ x , ax 1 ~ x ln a , 1 x ~ ax .
Теорема о замене бесконечно малых эквивалентными при вычислении пределов
Теорема (о замене б/м на эквивалентные в отношениях): Пусть x ~ 1 x ,
x ~ |
x эквивалентные б/м при x x |
. Тогда |
lim |
x |
lim |
1 |
x . |
||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
1 |
x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
x x0 |
||||||
Доказательство. Рассмотрим |
lim |
x |
. Тогда, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim |
x 1 |
x 1 x |
lim |
|
x |
lim |
1 |
x |
lim |
1 |
x |
lim |
1 |
x |
. |
|
|
|
|
||||
x 1 |
x 1 x |
|
|
|
|
|
x |
|
x |
|
x |
|
|
|
|
||||||||
x x0 |
x x0 |
1 |
x x x0 |
|
x x0 |
1 |
x x0 |
1 |
|
|
|
|
|
||||||||||
Производная, её геометрический и механический смысл
Геометрический смысл производной состоит в том, что значение производной функции y=f(x) в точке хо равно угловому коэффициенту касательной к графику функции в точке с абсциссой Хо: f'(x0) = k = tga
Уравнение касательной и нормали к графику функции

Дифференцируемость функции, дифференциал
Функция f(x) называется дифференцируемой в точке х0, если её приращение в этой точке может быть представлено в виде
дельта f(x0)= f(x0 + дельта x) - f(x0) = A*дельта x+ о(дельта x), где А - некоторое число; о(дельта х) - бесконечно малая функция более высокого порядка малости, чем дельта х при х -> 0.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента). 
Необходимое и достаточное условие дифференцируемости
Геометрический смысл дифференциала
Дифференциал функции двух переменных равен приращению аргумента аппликаты касательной плоскости.
Приближенные вычисления с помощью дифференциала

Непрерывность дифференцируемой функции
Теорема. Если функция y = f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом, из дифференцируемости функции следует ее непрерывность.
Доказательство. Если  , то
, то 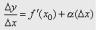
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при x→0. Но
тогда y=f '(x0) x+αΔx=> y→0 при x→0, т.е f(x) – f(x0)→0 при x→x0, а это и означает, что функция f(x) непрерывна в точке x0. Что и требовалось доказать.
Производная суммы, произведения и частного

Производная сложной функции
Производная обратной функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
I. Если x D (D – область определения) поставлен в соответствие |
y E , говорят, |
||||||||||||||||||||||||||||||||||||||||||||||
задана функция |
y f x . Если это взаимно однозначно, то можно рассмотреть |
||||||||||||||||||||||||||||||||||||||||||||||
функцию x x y , которая y ставит в соответствие x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Теорема: Пусть |
y y(x) и x x y |
взаимно обратные функции, тогда |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
y x |
|
1 |
|
|
|
или x y |
1 |
|
. Доказательство. Пусть обе функции |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
x y |
|
y x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
дифференцируемы в некоторой точке. |
|
Тогда, |
lim |
y |
lim |
|
1 |
|
|
|
, т.к. обе функции |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
x |
|
x 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дифференцируемы непрерывны, т.е. |
y 0 |
|
при x 0 . Тогда, |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
lim |
|
1 |
lim |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x 0 x |
y 0 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производные обратных тригонометрических функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
а) |
y arcsin x , |
x sin y , тогда |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 sin |
2 |
|
1 x |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
б) |
y arccos x |
, x cos y , |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
arccos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin y |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 cos y |
|
|
|
|
|
1 x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в) y arctgx , |
x tgy , |
|
|
1 |
|
2 |
1 |
1 , |
|||
|
|
arc tgx |
|
|
cos |
|
y |
1 tg 2 y |
|
1 x2 |
|
|
|
|
|
tgy |
|
|
|
|
|
|
|
г) |
y arcctgx , |
x ctgy , |
|
|
1 |
|
2 |
1 |
1 . |
|||
|
|
|
arc ctgx |
|
|
sin |
|
y |
1 ctg 2 y |
|
1 x2 |
|
|
|
|
|
|
ctgy |
|
|
|
|
|
|
|
Параметрическое задание функции
Пара уравнений x = x(t) и y= y(t) где t- вспомогательная переменная, задаёт некоторую линию. Этот способ задания линии называется параметрическим, а переменная t- параметром. Исключая t получаем обычное уравнение той же линии: y= y (g(x))
Производные первого и второго порядка функций, заданных параметрически
I. Производной 2-го порядка от функции y f x называется производная от ее первой производной: y y . Вообще, производной n-го порядка называется производная от производной порядка n-1: yn yn 1 .
II. Пусть функция y f x дифференцируема, тогда приращение функции
y f x dx dx dx , следовательно dy f x dx - дифференциал I-го порядка.
Рассмотрим 1-й случай, когда x – независимая переменная. Тогда dx - число. Предполагая, что функция y f x дифференцируема дважды в т. x, найдем дифференциал от дифференциала I-го порядка при dx1 dx :
|
|
|
|
|
|
|
dx1 , |
|
d |
2 |
y f x dx |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
d f x dx f x |
|
|
|
|
- полученное выражение при |
|||||||||||||||||||||||||
dx1 dx называется дифференциалом II-го порядка. Аналогично: |
d 3 y f x dx3 , |
|||||||||||||||||||||||||||||
d n y f n x dxn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим 2-й случай, когда x x t , а |
y f x t |
- соответственно сложная |
||||||||||||||||||||||||||||
функция. Тогда |
dy f x dx - дифференциал I-го порядка, а dx - функция, |
|||||||||||||||||||||||||||||
|
|
|
|
|
Тогда: d |
2 |
y d f |
|
x dx , d |
2 |
y d f |
|
x dx |
d dx f |
|
x , |
||||||||||||||
dx x t dt . |
|
|
|
|
|
|
||||||||||||||||||||||||
d |
2 |
y f |
|
|
|
t dt |
2 |
f |
|
x , d |
2 |
y f |
|
x dx |
2 |
f |
|
x d |
2 |
x . |
|
|
||||||||
|
|
x dxdx x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Дифференциалы 2-го (и более высокого порядка) не обладают инвариантностью формы (т.е. меняют вид в зависимости от x).

Касательная к кривой, заданной параметрически
Производные и дифференциалы высших порядков
I. Производной 2-го порядка от функции y f x называется производная от ее первой производной: y y . Вообще, производной n-го порядка называется
производная от производной порядка n-1: yn yn 1 .
II. Пусть функция y f x дифференцируема, тогда приращение функции
y f x dx dx dx , следовательно dy f x dx - дифференциал I-го порядка.
Рассмотрим 1-й случай, когда x – независимая переменная. Тогда dx - число. Предполагая, что функция y f x дифференцируема дважды в т. x, найдем
дифференциал от дифференциала I-го порядка при dx1 dx : d f x dx |
|
|
||||||||||
f x dx1 |
||||||||||||
, d 2 y f x dx2 |
- полученное выражение при dx1 dx называется дифференциалом |
|||||||||||
II-го порядка. Аналогично: d 3 y |
f x dx3 , |
d n y f n x dxn . |
|
|
||||||||
Рассмотрим 2-й случай, когда x x t , а |
y f x t |
- соответственно сложная |
||||||||||
функция. Тогда |
dy f x dx - дифференциал I-го порядка, а dx - функция, |
|||||||||||
|
|
2 |
y d f |
|
x dx , d |
2 |
y d f |
|
x dx d dx f |
|
x , |
|
dx x t dt . Тогда: d |
|
|
|
|
|
|||||||
d 2 y f x dxdx x t dt2 f x , |
d 2 y |
f x dx2 f x d 2 x . Дифференциалы 2-го |
||||||||||
(и более высокого порядка) не обладают инвариантностью формы (т.е. меняют вид в зависимости от x).
