
DiskretPDF
.pdf19. Сети и потоки. Величина потока и его свойства (сумма потоков из источника = сумме потоков в сток). Задача о нахождении максимального потока.
Определение. Сетью называется взвешенный граф G = (E, V) с весовой функцией q : E → R+ в котором выделен источник A V,→deg(A) = 0, и сток B V, ←deg(B) = 0. Значение q(X, Y) называется пропускной способностью ребра (X, Y) E.
Если (X, Y) / E то считаем, что q(X, Y) = 0
Определение. Потоком называется весовая функция p : E → R+ {0} такая, что
1.p(X, Y) ≤ q(X, Y) для всех (X, Y) E;
2.Для всех вершин C != A,B имеет место
|
|
(С, X ) E |
(Y ,C) E |
p(C, X) = |
p(Y, C). |
Если (X, Y) / E то считаем, что p(X, Y) = 0.Теорема. Для потока p : E 7→ R+ в сети G = (E, V, q, A, B)
имеет место
|
|
|
|
|
|
|
|
|
( А, X ) E |
(Y,B) E |
|
|
|
|
|
|
|
p(A, X) = |
|
p(Y, B). |
|
|
|
|
|
|
Данная сумма называется величиной потока. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
( А, X ) E |
|
(C, X ) E |
C A,B (C, X ) E |
|
(Y ,C) E |
C A,B (Y ,C) E |
||
p(A, X) = |
C V |
p(C, X) − |
|
|
p(C, X) =C V |
p(Y, C) − |
|
p(Y, |
C) =
(Y,B)
p(Y, B).
Задача о максимальном потоке.
Дано. Пусть имеется сеть G = (E, V, q, A, B).
Найти поток p : E → R+ {0} с наибольшей величиной V(p).
Алгоритм
Пусть к этому шагу в транспортной сети G, c построен поток f и сток получил пометку (m+, δ). Тогда увеличиваем поток fms через дугу (m, s) и полагаем его равным f’ms = fms +δ. Переходим к рассмотрению вершины m. Общий шаг: пусть находимся в вершине j . Возможны две ситуации: вершина имеет метку вида (i+, γ), либо вершина имеет метку вида (i−, γ). Тогда в первом
случае, изменяем поток f’ij = fij + δ, а во втором случае (здесь дуга идет из j в i) полагаем поток равным f’ji = fji − δ (необходимо обратить внимание на то, что поток через дугу на каждом шаге изменяется на одну и ту же величину δ). В обоих случаях переходим к вершине i. Продолжаем изменение потока, пока не достигнем источника. Как только источник достигнут, переходим к этапу расставления пометок.
20. Разрезы в сетях. Величина потока не превосходит величины разреза. Величина разреза.
Определение. Разрезом в сети G = (E, V, q, A, B) называется произвольное подмножество U V такое, что A U и B / U.
Определение. Величина потока через разрез: V(p, U) = V+(p, U) − V−(p, U),
|
|
где V+(p, U) = |
Y U , X U |
p(Y, X), |
|
|
V−(p, U) = |
Y U , X U |
p(X, Y). |
Теорема. Для потока p : E → R+ {0} в сетиG = (E, V, q, A, B) и произвольного разреза U V имеет
место V(p, U) = V(p).
Доказательство. Индукция по |U|. Если |U| = 1, то U = {A}, V−(U, p) = 0и V+(U, p) = V(p).
Предположим, что теорема верна при |U| = n. Докажем теорему при |U| = n + 1. Пусть U = W C},
C != A, B и |W| = n. По предположению V(W, p) = V(p).
Тогда V(U, p) − V(W, p) =(V+(U, p) − V+(W, p)) − (V−(U, p) − V−(W, p)) =
|
|
|
|
|
|
( X U |
p(C, X) −Y U |
p(Y, C))−( Y U |
p(Y, C) − X U |
p(C, X))= X |
p(C, X) − Y p(Y, C) = 0. |
Значит, V(U, p) = V(W, p) = V(p). |
|
|
|||
21. Алгоритм Форда-Фолкерсона.
Пусть дана транспортная сеть (G, c). Работа алгоритма состоит из трех этапов. 1. Выбор исходного потока. Строим произвольный поток f в сети (G, c), например, нулевой.
2. Расставление пометок. Вершинам будут приписываться метки состоящие из двух элементов. На первом шаге, помечаем источник меткой (−, ∞). Очередной шаг: выбираем одну из уже помеченных, но еще не обработанных вершин (например, с наименьшим номером) и обрабатываем ее. Пусть требуется обработать
вершину i с пометкой (x, q), тогда действуем по следующим правилам:
- если из вершины i в не помеченную вершину j идет такая дуга, что fij < cij , то помечаем вершину j парой (i+, min(q, cij − fij));
- если в вершину i из не помеченной вершины j идет такая дуга, что fji > 0, то помечаем вершину j парой (i−, min(q, fji)).
После того как помечены все возможные на данном шаге вершины, переходим к следующему шагу.
Этап завершается в двух случаях:
- если помечен сток — в этом случае алгоритм переходит к этапу изменения потока; - если сток еще не помечен, и нельзя больше пометить ни одной вершины — в
этом случае алгоритм останавливается.
3. Изменение потока. Пусть к этому шагу в транспортной сети G, c построен поток f и сток получил пометку (m+, δ). Тогда увеличиваем поток fms через дугу (m, s) и полагаем его равным f0ms = fms +δ. Переходим к рассмотрению вершины
m. Общий шаг: пусть находимся в вершине j . Возможны две ситуации: вершина имеет метку вида (i+, γ), либо вершина имеет метку вида (i−, γ). Тогда в первом случае, изменяем поток f0ij = fij + δ, а во втором случае (здесь дуга идет из j в i) полагаем поток равным f0ji = fji − δ (необходимо обратить внимание на то, что поток через дугу на каждом шаге изменяется на одну и ту же величину δ). В обоих случаях переходим к вершине i. Продолжаем изменение потока, пока не достигнем источника. Как только источник достигнут, переходим к этапу расставления пометок.

22. Конечные автоматы и регулярные языки. Примеры регулярных и нерегулярных языков.
1.Алфавитом X называется произвольный набор символов.
2.Словом над X называется произвольный набор символов α = x1x2 . . . xl, где xiX. Число l называется длиной слова α. Пустое слово λ — слово длины 0.
3.Через X обозначается множество всех слов над алфавитом X. Если α, β X , то через αβ X
обозначается конкатенация слов α и β. α^n — конкатенация α с собой n раз.
4.Языком L над X называется любое подмножество X , то есть L X . Примеры языков.
1.X = {а, б, в, . . . , я};
L = {α X | α — слово русского языка}; мама, папа L; ммпа, аько / L.
2.X = {а, . . . , я} {,.!?;:-“”} {А, . . . , Я}; L = {α X | α — предложение русского языка};
Мама мыла раму. L; Мама мыло раме. / L.
Определение. Конечный автомат над — ориентированный граф A = (Q, E), ребра которого помечены функцией f : E → X таким образом, что для любого символа x X и любой вершины q Q существует и единственно ребро e E c началом q и меткой f(e) = x. Вершины конечного автомата называются состояниями. Тогда каждому состоянию q Q и символу x X однозначно сопоставлено состояние q 0 = δ(q, x), являющееся концом ребра с началом q и меткой x. Функция
δ : Q × X → Q называется функцией перехода.
Определение. Конечный автомат называется настроенным, если в нем выделено начальное состояние q0 Q и множество F Q допускающих состояний.
Определение. Настроенный автомат A = (Q, X, δ, q0, F) распознает язык L X , если для любого α X имеет место α L q0δ(α) F.
Определение. Язык L X называется регулярным, если он распознается некоторым (настроенным) конечным автоматом.
Примеры.
1.
2.
3.
23. Отношение различимости слов заданным языком. Ранг языка. Теорема Майхилла-Нероуда.
Бинарное отношение на множестве M называется отношением эквивалентности
если для всех x, y, z M выполнены следующие условия: 1. X x (рефлексивность);
2. x y и y z = x z (транзитивность); 3. x y = y x (симметричность).
Фактор-класс элемента x M : [x] = {z M | x z}. Тогда [x] = [y] [x] ∩ [y]
6= x y. Множество M разбито на непересекающиеся фактор-классы. Множество всех фактор-классов M/ = {[x] | x M} называется фактор-
множеством
Пусть задан язык L X . Говорим, что слова α, β X неразличимы относительно L(α L β), если
αε L βε L для любого ε X .
Примеры. Для языка L = {a, aab, aba, bb} имеем
1.a 6 L b, так как a L и b / L;
2.a 6 L aba, так как a ba L и aba ba / L;
3.aa 6 L bb, так как aa b L и bb b / L;
4.aba L bb, так как aba L, bb L, abaε / L, bbε / L при ε != λ;
5.aa L b, так как aa / L, b / L, , aa b L, b b L, aaε / L, bbε / L при ε 6= λ,
b;
Бинарное отношение L является отношением эквивалентности:
1.α L α;
2.α L β и β L γ = α L γ;
3.α L β = β L α.
Кроме того выполнено условие конгруэнтности:
4.α L β = αγ L βγ.
Фактор-класс строки α X обозначается через [α]L = {β X | x z}. Количество элементов в фактор множестве X / L= {[α]L | α X } называется рангом языка L, обозначаемого через rk L
Теорема Майхилла-Нероуда
Теорема. Язык L распознается конечным автоматом с n состояниями тогда и только тогда,
когда rk L ≤ n
Пусть rk L ≤ n. Построим автомат c Q = X / L, q0 = [λ]L, F = {[α]L | α L} и [α]Lδx = [αx]L.
Тогда при α = x1 . . . xk F 3 [λ]Lδ(α) = [λ]Lδ(x1 . . . xk) = [x1 . . . xk] L = [α]L α L,
то есть автомат распознает L.
Следствие. Минимальное количество состояний в автомате, распознающим регулярный язык, равно рангу этого языка.

?24. Регулярность объединения и пересечения языков.
Произведение конечных автоматов
Операции объединения и пересечения регулярных языков Теорема. Дополнения, объединения и пересечения регулярных языков снова являются регулярными языками

?25. Недетерминированные автоматы и распознаваемые ими языки.

?24.1 Регулярность конкатенации и L*.
Недетерминированный автомат для L
26. Регулярные выражения.
Для обозначения регулярных языков удобно использовать регулярные выражения. Каждый регулярный язык можно записать в виде строки, содержащей символы алфавита, символ , круглые и фигурные скобки, и символы и .
На пример, L = (({0} {1}) ) ({0}{1}) – регулярный язык, принадлежащий классу R4 . Регулярным выражением для заданного регулярного языка называется строка, полученная удалением фигурных скобок в записи этого языка. Так регулярным выражением для рассмотренного выше языка L будет строка ((0 1) ) (01). Для каждого языка существует бесконечно много регулярных выражений. Например, строка ((0 1) ) (01) является регулярным выражением для того же языка L. Приведем более строгое определение регулярных выражений по индукции.
Определение. Регулярные выражения в алфавите Σ и регулярные языки, для обозначения которых они служат, определяются следующим образом:
1.– регулярное выражение, обозначающее пустой язык,
2.если x Σ, то x – регулярное выражение, обозначающее язык {x},
3.если p и q – регулярные выражения, обозначающие языки P и Q соответственно, то
• (pq) – регулярное выражение, обозначающее язык P Q,
• (p q) – регулярное выражение, обозначающее язык P Q,
• (p) – регулярное выражение, обозначающее язык P ,
4.других регулярных выражений в языке Σ нет.
Подобно арифметическим выражениям, в регулярных выражениях можно опускать скобки, назначив приоритет каждой операции. Принято считать, что самый высокий приоритет у звездочки Клини, более низкий у конкатенации, и самый низкий у объединения. Так опуская скобки в регулярном выражении ((0 1) ) (01), получим строку (0 1) 01.
Теорема Клини. Язык над алфавитом X является регулярным тогда и только тогда, когда он может быть выражен через языки , {λ}, {a}, где a X, и операции , ·и .

27. Машины Тьюринга. Вычислимые языки. Тезис Черча-Тьюринга. Вычислимость регулярных языков.
Машина Тьюринга определяется кортежем вида
где 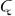 — конечное множество состояний;
— конечное множество состояний; 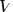 — конечный входной алфавит;
— конечный входной алфавит;  — символ, называемый маркером начала ленты;
— символ, называемый маркером начала ленты; 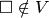 — символ, называемый пустым (или пробелом);
— символ, называемый пустым (или пробелом); 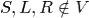 — символы, называемые символами направления движения головки;
— символы, называемые символами направления движения головки; 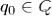 — начальное состояние;
— начальное состояние; 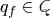 — заключительное состояние;
— заключительное состояние; 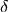 — функция переходов, являющаяся отображением вида причем значение
— функция переходов, являющаяся отображением вида причем значение 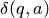 , коль скоро оно определено, есть конечное (возможно, и пустое) множество упорядоченных троек из соответствующего декартова произведения.
, коль скоро оно определено, есть конечное (возможно, и пустое) множество упорядоченных троек из соответствующего декартова произведения.
Функция переходов может быть записана в виде системы команд. Каждая команда есть слово вида
где |
. |
Слово (до стрелки) называется левой частью команды, а слово |
(после стрелки) — правой |
частью команды. |
|
Неформально работу машины Тьюринга можно представить следующим образом. Машина имеет устройство управления, которое может находиться в одном из состояний множества 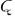 , полубесконечную ленту, разделенную на ячейки, в каждой из которой может быть записан символ из
, полубесконечную ленту, разделенную на ячейки, в каждой из которой может быть записан символ из
алфавита 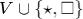 , причем крайняя левая ячейка хранит символ
, причем крайняя левая ячейка хранит символ  , и головку чтениязаписи, которая в каждый момент дискретного времени обозревает какуюто одну ячейку ленты. Символ
, и головку чтениязаписи, которая в каждый момент дискретного времени обозревает какуюто одну ячейку ленты. Символ  (пробел) не следует путать с пустой цепочкой — это специальный символ, означающий пустую, т.е. не
(пробел) не следует путать с пустой цепочкой — это специальный символ, означающий пустую, т.е. не
хранящую символов алфавита 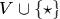 , ячейку ленты. Команда, записанная выше, разрешает машине Тьюринга, устройство управления которой находится в состоянии
, ячейку ленты. Команда, записанная выше, разрешает машине Тьюринга, устройство управления которой находится в состоянии 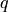 , а головка обозревает ячейку, хранящую символ
, а головка обозревает ячейку, хранящую символ  , перевести устройство управления в состояние
, перевести устройство управления в состояние  , записав в обозреваемую ячейку символ
, записав в обозреваемую ячейку символ 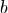 (который может и совпадать с
(который может и совпадать с  ), и оставить головку на прежнем месте, если
), и оставить головку на прежнем месте, если 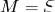 , сдвинуть ее на одну ячейку влево, если
, сдвинуть ее на одну ячейку влево, если 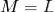 , или на одну ячейку вправо, если
, или на одну ячейку вправо, если 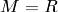 .
.
Будем говорить, что машина Тьюринга применима к слову |
, если из |
||||
конфигурации |
выводится конфигурация |
для некоторого |
. |
||
Слово будем называть в этом случае результатом применения машины Тьюринга к слову и |
|||||
обозначать его |
. Факт применимости машины к слову будем обозначать |
; если же не |
|||
применима к , то будем записывать |
. |
|
|
|
|
Множество всех слов , таких, что |
, называется областью применимости машины Тьюринга . |
||||
Словарная функция в алфавите |
называется вычислимой по Тьюрингу, если |
||||
существует такая машина Тьюринга |
с входным алфавитом |
, содержащим , что |
|||
Тезис Черча-Тьюринга - для любой интуитивно вычислимой функции существует вычисляющая её значения машина Тьюринга.
