DiskretPDF

10. Неориентированные графы. Степени вершин. Сумма степеней вершин графа. Изоморфизм

графов. Пример неизоморфных графов с одинаковыми степенями.

Определение. Неориентированный граф состоит из множества вершин V и множества ребер E, причем каждому ребру e E сопоставлена неупорядоченная пара вершин a, b.

Определение. Ребро, сопоставленное паре {a, a} называется петлей. Если несколько ребер сопоставлены одной и той же паре вершин {a, b}, то такие ребра называют кратными.

Определение. Неориентированный граф (V, E) называется простым, если среди элементов V нет петель и кратных ребер. Для случая простых графов мы будем отождествлять ребра e E с соответствующей парой вершин {a, b} V^2.

Определение. Если ребру e E сопоставлена пара вершин {a, b} V^2, то будем говорить, что ребро e инцидентно каждой из вершин a и b.

Определение. Если имеется ребро e E, сопоставленное паре вершин {a, b} V^2, то будем говорить, что вершины a и b являются

смежными.

Определение. Степенью вершины deg(j) неориентированного графа называют количество инцидентных вершине j ребер, при этом каждая инцидентная ей петля считается два раза. Другими словами, deg(j) =

Теорема. Сумма степеней всех вершин неориентированного графа равна удвоенному количеству ребер,

Доказательство. 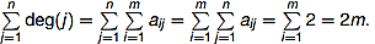Определение. Неориентированные графы G = (V, E) и G’ = (V’, E’) изоморфны, если существуют биективные отображения f : V → V’ и g : E → E’ такие, что e E инцидентна a V g(e) E’ инцидентна f(a) V’.

Для случая простых графов для изоморфизма достаточно существования биективного отображения f : V → V’ такого, что

a, b V — смежные f(a), f(b) V’ — смежные.

Для изоморфных графов G и G’ имеем deg(a) = deg(f(a)).

11. Связные графы и компоненты связности. Неравенство между количеством вершин, ребер и компонент связности.

Определение. Вершины A и B графа G = (V, E,) называются связанными, если существует путь из А в В.

Отметим, что можно считать этот путь цепью. Граф G называется связным, если любые его две вершины связанны.

Компонентой связности графа G = (V, E) называется любое связное непустое подмножество K V, такое что не существует ребер с началом a K и концом b

K.

Определение. Ребро графа G = (V, E,) называется мостом, если его удаление приводит к увеличению числа компонент связности. (при этом увеличение может быть только на единицу).

Теорема. Пусть в графе G = (V, E) имеется ровно n вершин, m ребер и k компонент связности. Тогда m + k ≥ n.

Доказательство. Индукция по m. Пусть m = 0. Тогда k = n, и m + k = k = n ≥ n. Предположим, что теорема верна, если количество ребер равно m − 1, m > 0. Докажем теорему для m. Для этого удалим из G какое-нибудь ребро e. Получим граф G’ c m−1 ребром, n вершинами и k’ компонентами связности. При этом k’ − k ≤ 1. По предположению индукции имеем (m − 1) + k’ ≥ n. Тогда

m + k ≥ m + (k’ − 1) = (m − 1) + k’ ≥ n.

12. Эйлеровы и гамильтоновы пути. Критерий существования эйлерового пути.

Определение. Пусть дан граф G = (V, E,) и количество ребер равно m . Эйлеровым путем называется замкнутый путь длины m состоящий из различных ребер без повторений. Если условие замкнутости убрать, то получим определение полуэйлерового пути.

Определение. Пусть дан граф G = (V, E,) и количество вершин равно n . Гамильтоновым путем называется замкнутая цепь длины n. Если условие замкнутости убрать, то получим определение полугамильтонового пути. Теорема. Связный граф имеет эйлеров путь тогда и только тогда, когда степени всех вершин четны.

Теорема. Связный граф имеет полуэйлеров путь тогда и только тогда, когда имеется только две вершины с нечетными степенями.

Доказательство. Предположим граф содержит эйлеров цикл. Пройдем по этому циклу, тогда вершина посещенная k раз (за исключением начальной) должна иметь степень 2k , так как при каждом посещении по одному ребру входим и по одному выходим, увеличивая степень вершины на 2. Для начальной вершины, при первом посещении только выходим по некоторому ребру, а при последнем только входим, следовательно, степень будет равна 2(k − 1).

Пусть степени всех вершин чётны. Рассмотрим цепь максимальной длины: C = v0e0v1e1 . . . ekvk+1.

Все ребра инцидентные vk+1 уже встречаются в этой цепи, иначе её можно было бы

продолжить. По предположению, число таких ребер четно, следовательно vk+1 =v0 , так как ek инцидентно vk+1 , а все остальные вхождения vk+1 увеличивают степень вершины на 2. Предположим, что C не эйлеров цикл. Тогда существует ребро e’ не принадлежащее циклу C . Eсли e’ не инцидентно никакой вершине цикла C , то рассмотрим путь соединяющй, например, вершину v0 и один из концов ребра e’ и выберем первое ребро e не принадлежащее циклу C . Тогда это рeбро

ицидентно некоторой вершине vi цикла, и пусть имеет вид e = {vi, u}.

Тогда цепь C’ = ueviei. . . ekvk+1e0v1, . . . vi−1ei−1vi имеет длину большую чем C , что противоречит выбору C .

13. Леса и деревья. Эквивалентность различных определений.

Определение. Граф G = (V, E,) называется лесом, если он не содержит циклов.

Теорема . Пусть в графе G = (V, E) имеется ровно n вершин, m ребер и k компонент связности. Тогда следующие условия эквивалентны:

1. G — лес;

2. каждое ребро из G — мост.

3. каждая цепь, соединяющая две вершины, единственна;

4. m+k=n;

Определение. Связный лес называется деревом.

Теорема. Пусть в связном графе G = (V, E) имеется ровно n вершин и m ребер. Тогда следующие условия эквивалентны:

1 G — дерево;

2 каждое ребро из G — мост.

3 каждая цепь, соединяющая две вершины, единственна;

4 m+1=n;

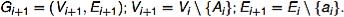
14. Теорема Кэли о количестве деревьев на n вершинах. Коды Прюфера.

Теорема (Кэли). Имеется ровно n^(n−2) деревьев с множеством вершин V = {1, 2, . . . , n}.

Определение. Рассмотрим следующую процедуру для дерева G = (V, E):

1.G1 = G.

2.Пусть дано дерево Gi = (Vi, Ei), Выберем наименьшую вершину Ai Vi степени 1.

Пусть a Ei — единственное ребро, соединяющее Ai с некоторой вершиной Bi. Определяем дерево

Последовательность B1, B2, . . . Bn−2 называется кодом Прюфера дерева G. Теорема. (Кэли). Каждая последовательность B1, B2, . . . , Bn−2, где Bi = 1..n, является кодом

Прюфера в точности одного дерева с вершинами {1, . . . , n}. Доказательство. Если c является кодом Прюфера некоторого дерева G с вершинами {1 . . . n}, то дерево состоит из ребер {Ai, Bi}, i = 1..n − 1, где

1.A1 — наименьшее число, отличное от B1, B2, . . . , Bn−2;

2.Ai, i = 2..n − 2, — наименьшее число, отличное от A1, . . . Ai−1, Bi, . . . , Bn−2;

3.An−1 — наименьшее число, отличное от A1, . . . An−2;

4.Bn−1 — наименьшее число, отличное от A1, . . . An−1.

15. Алгоритм Краскала нахождения остова наименьшего веса.

Пусть дан связный граф G = (V, E) с n вершинами и m ребрами. Тогда m ≥ n − 1. Если m = n − 1, то G является деревом. Если m > n − 1, то в G имеется ребро e E, не являющееся мостом.

Определение. Взвшенный граф — граф G = (V, E) с заданной функцией µ : E → R. Величина µ(e) называется весом ребра e E. Задача. По данному связному взвешенному графу G = (V, E, µ) найти остов T = (V, P) такой, что вес остова

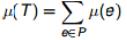наименьший.

Алгоритм Краскала.

Пусть задан связный взвешенный граф G = (V, E, µ) с n вершинами.

Определим P0 = . Повторим следующую процедуру для каждого k = 1, 2, . . . n − 1.

1.Пусть Pk−1 = {e1, e2, . . . ek−1} уже определено.

2.Найдем ребро ek E \ Pk−1 наименьшего веса такое, что ребра e1, e2, . . .

ek−1, ek не образуют циклов.

3 Определим Pk = {e1, e2, . . . ek−1, ek}.

Дерево T = (V, P), где P = Pn−1, является искомым остовом наименьшего веса. Обоснование алгоритма. Докажем, что µ(T) ≤ µ(U) для произвольного остова U = (V, S) взвешенного графа G = (V, E, µ). Предположим, что для некоторых остовов указанное неравенство не

выполняется. Назовем число k = 1, 2, . . . , n − 1 степенью близости остова U = (V, S), если k — наибольшее число такое, что e1, e2, . . . ek S. Выберем остов U = (V, S) наибольшей возможной степени близости k, что µ(T) > µ(U). Имеем k < n − 1, e1, . . . , ek S и ek+1 ! S.

Тогда среди ребер S {ek+1} можно выбрать цикл, содержащий также ребро eS, e 6= e1, . . . , ek. По алгоритму имеем µ(ek+1) ≤ µ(e).

Тогда U’ = (V, S’), S’ = (S {ek+1}) \ {e} имеет степень близости > k, но µ(T) > µ(U) ≥ µ(U’).

16. Плоские графы. Грани плоских графов. Формула Эйлера для плоских графов.

Определение. Граф называется плоским, если он представим в пространстве R^2.

Определение. Гранью в плоском представлении называется часть пространства R^2, отделенная дугами этого представления.

Теорема (формула Эйлера). Количество граней в плоском представлении связного графа с n вершинами и m ребрами равно m − n + 2.

Следствие. Количество граней в плоском представлении графа с n вершинами , m ребрами и k компонентами связности равно m − n + k + 1.

Доказательство формулы Эйлера для плоских связных графов

Индукция по величине t = m − n ≥ −1. База индукции: если t = m − n = −1, то граф является

деревом и количество граней равно 1 − 1 + 2 = m − n + 2.

Индукционное предположение: предположим формула Эйлера верна для всех плоских представлений с m − n = t.

Индукционное шаг: пусть дано плоское представление G = (V, E) с n вершинами и m ребрами, причем

m − n = t + 1 ≥ 0. Тогда G не является деревом, и содержит ребро e E не являющееся мостом. Тогда граф U = (V, E \ {e}) по индукционному предположению имеет (m − 1) − n + 2 граней.

Но поскольку e содержалось в некотором цикле, количество граней в U на единицу

меньше чем в G. (m − 1) − n + 2 + 1 = m − n + 2 граней.

17 Ориентированные графы. Положительные и отрицательные степени вершин. Теорема о суммах положительных и отрицательны степеней.

Изоморфизм ориентированных графов.

Определение. Ориентированный граф состоит из множества вершин V и множества ребер E, причем каждому ребру e E сопоставлена упорядоченная пара вершин (a, b) V^2.

В этом случае говорят, что вершина a V является началом, а b V — концом ребра e E.

Определение. Ребро, сопоставленное паре (a, a) называется петлей. Если несколько ребер имеют одинаковое начало и конец, то такие ребра называют

кратными.

Определение. Неориентированный граф (V, E) называется простым, если среди элементов V нет петель и кратных ребер. Для случая простых графов мы будем отождествлять ребра e E с соответствующей парой вершин (a, b) V^2.

Определение. Путь из A V в B V во взвешенном графе G = (V, E) с весовой функцией w : E 7→ R+ называется минимальным, если его длина не превосходит длины любого другого пути из A V в B V.

Определение. Расстоянием d(A, B) из A V в B V во взвешенном графе G = (V, E) называется длина

минимального пути из A в B. Если путей из A в B нет, то d(A, B) = ∞.. Степень захода вершины v орграфа D = (V, A) определяется следующим образом

d+D(v) = |{u V | (u, v) A}|.

Степень исхода вершины v орграфа D = (V, A) определяется следующим образом d−D(v) = |{u V | (v, u) A}|.

Имеет место следующий аналог леммы о рукопожатиях.

Лемма 7. Если D = (V, A) ориентированный граф, то v V d−D(v).

Орграфы G = (V, E) и G’ = (V’, A’) называются изоморфными, если существует такая биекция

ϕ : V → V’, что (u, v) A (ϕ(u), ϕ(v)) A’. Отображение ϕ называется изоморфизмом.

Таким образом, как и в случае неориентированных графов, изоморфизм это биективное отображение множества вершин при котором смежным вершинами графа G соответствуют смежные вершины графа G’ и наоборот и, кроме того, сохраняются направления дуг.

18. Алгоритм Дейкстры нахождения кратчайшего пути.

Формальное определение

Дан взвешенный ориентированный граф G(V,E) без петель и дуг отрицательного веса.

Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины

до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация.

Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это

отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из

ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы

рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом.

Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа

вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме

значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки

полученным значением

длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

Доказательство корректности

Пусть l(v) — длина кратчайшего пути из вершины a в вершину v. Докажем по индукции,

что в момент посещения любой вершины z, d(z)=l(z).

База. Первой посещается вершина a. В этот момент d(a)=l(a)=0.

Шаг. Пускай мы выбрали для посещения вершину z != a. Докажем, что в этот момент d(z)=l(z).

Для начала отметим, что для любой вершины v, всегда выполняется d(v) >= l(v) (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть P — кратчайший путь из a в z, y — первая непосещённая вершина на P, x

—

предшествующая ей (следовательно, посещённая). Поскольку путь P кратчайший, его часть,

ведущая из a через x в y, тоже кратчайшая, следовательно l(y)=l(x)+w(xy). По предположению индукции, в момент посещения вершины x выполнялось d(x)=l(x),

следовательно, вершина y тогда получила метку не больше чем d(x)+w(xy)=l(x) +w(xy)=l(y).

Следовательно, d(y)=l(y). С другой стороны, поскольку сейчас мы выбрали вершину z, её

метка минимальна среди непосещённых, то есть d(z)<=d(y) = l(y)<=l(z). Комбинируя это

с d(z)>=l(z), имеем d(z)=l(z), что и требовалось доказать. Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент d=l для всех вершин.