Сборник задач

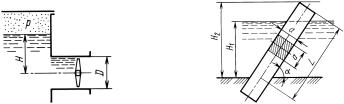
К задаче 2.24

К задаче 2.25

Найти равнодействующую P сил давления на этот же брус дли-

ной L = 8 м при глубине дна H2

= 6 м (весь брус под водой).

Ответ. Возникает пара сил,

момент которой M = 27,7 кН ∙ м;

Глава 3. СИЛЫ ДАВЛЕНИЯ

ПОКОЯЩЕЙСЯ ЖИДКОСТИ

НА КРИВОЛИНЕЙНЫЕ

СТЕНКИ. ПЛАВАНИЕ ТЕЛ

ВВЕДЕНИЕ

Распределенная нагрузка на криволинейную поверхность от сил

давления жидкости, нормальных к этой поверхности в каждой ее

точке, может быть приведена к главному вектору и главному момен-

ту. Главный вектор определяется по трем составляющим (обычно

по вертикальной и двум взаимно перпендикулярным горизонталь-

ным составляющим), главный момент – по сумме моментов этих

составляющих.

Для криволинейных стенок, симметричных относительно вер-

тикальной плоскости (большинство практических задач),

сумма

элементарных сил давления приводится к одной равнодействую-

щей силе, лежащей в плоскости симметрии, или к паре сил, ле-

жащей в той же плоскости. Величина и направление равнодей-

ствующей силы P определяются по двум составляющим, обычно

горизонтальной и вертикальной, как показано на рис. 3.1.

Горизонтальная составляющая силы давления, воспринимае-

мой криволинейной стенкой, равна силе давления на вертикаль-

ную проекцию этой стенки, нормальную к плоскости симметрии, и

определяется по формуле

где

Pг = ρghCFв,

(3.1)

ρ – плотность жидкости; g – ускорение свободного падения;

hC –

расстояние по вертикали от центра тяжести вертикальной про-

Линия действия силы Pг, проходя через центр давления верти-

кальной проекции стенки, лежит в плоскости симметрии и смещена

(вниз, если hC > 0, или вверх, если hC

< 0) относительно центра

тяжести вертикальной проекции на расстояние

h =

JC

,

(3.2)

FвhC

где JС – момент инерции площади вертикальной проекции относи-

тельно горизонтальной оси, проходящей через центр тяжести про-

екции.

Вертикальная составляющая силы давления, воспринимаемой

криволинейной стенкой, равна силе тяжести жидкости в объеме V ,

который ограничен стенкой, пьезометрической плоскостью и вер-

тикальной проектирующей поверхностью, построенной на контуре

стенки, и определяется но формуле

(3.3)

Pв = ρgVв.

Рис. 3.1

Сила Pв проходит через центр тяжести объема Vв и направлена

вниз, если объем строится со смоченной стороны стенки, и вверх –

если объем строится с несмоченной стороны стенки.

В формулах (3.1) и (3.3) для Pг и Pв предполагается, что жид-

кость находится с одной стороны стенки, а с несмоченной ее сторо-

ны давление равно атмосферному.

Полная сила давления на стенку представляет геометрическую

сумму сил Pг и Pв:

P = pPг + Pв.

(3.4)

53

Линия действия силы P проходит через точку пересечения ли-

ний действия сил Pг и P .

Угол ϕ наклона равнодействующей к горизонту определяется из

формулы

tg ϕ =

Pв

.

(3.5)

Pг

Для стенок постоянной кривизны (цилиндрических, сфериче-

ских) полная сила давления проходит через центр или ось кривизны

стенки.

При избыточном давлении на смоченной стороне стенки все со-

ставляющие и полная сила давления жидкости направлены от жид-

кости на стенку (изнутри наружу).

В случае разрежения на смоченной стороне стенки силы напра-

влены снаружи внутрь сосуда.

При двустороннем воздействии жидкостей на стенку сначала

определяются горизонтальные и вертикальные составляющие с

каждой стороны стенки в предположении одностороннего воздей-

ствия жидкости, а затем суммарные горизонтальная и вертикальная

составляющие от воздействия обеих жидкостей.

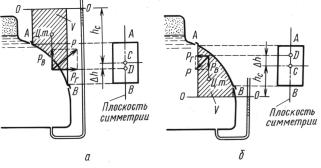
На рис. 3.2 показано определение горизонтальной и вертикаль-

ной составляющих и полной силы давления жидкости на симме-

тричную стенку АВ при избыточном давлении

(а) и при разреже-

нии (б) на смоченной стороне стенки.

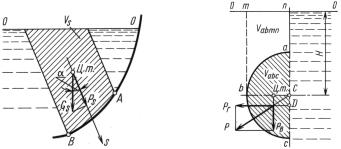
Сила давления жидкости на стенку по любому заданному напра-

влению s (рис. 3.3)

Ps = Gs cos α = ρgVs cos α,

(3.6)

Рис. 3.3

Рис. 3.4

Линия действия силы Ps проходит через центр тяжести жидко-

сти в объеме Vs.

В некоторых случаях для нахождения той или иной составляю-

щей силы давления жидкости на стенку следует разбить ее поверх-

ность на отдельные участки, определить соответствующие усилия

на каждый участок стенки и далее просуммировать их.

Так, для определения вертикальной составляющей силы давле-

ния жидкости на полусферическую стенку

abc (рис. 3.4) следует

Возможным приемом расчета силы

давления, который часто упрощает ре-

шение задач, является рассмотрение рав-

новесия объема жидкости,

заключенно-

го между стенкой и плоским сечением,

проведенным через ее граничный контур.

Пусть,

например, требуется определить

Рис. 3.5

силу P

давления жидкости на кониче-

скую крышку (рис. 3.5). Условие равнове-

сия объема жидкости, заполняющей конус, выражается векторным

уравнением

N + G + R = 0,

где

– сила давления жидкости на выделенный объем, т. е. на плос-

N

кое сечение ac (N = ρgHFac и проходит по нормали к сечению

через центр давления D);

– вес выделенного объема жидкости

G

(G = ρgV ); R –

сила действия конуса на жидкость.

Так как искомая сила P равна и противоположна силе R, полу-

чаем уравнение

(3.7)

P = N + G,

из которого можно определить силу давления

или любую ее со-

P

ставляющую.

Определить отрывающее и сдвигающее усилия и

Пример 1.

полную силу давления жидкости на полусферическую крышку ра-

диуса R, если заданы пьезометрический напор воды H

над центром

крышки и угол

α наклона стенки бака к горизонту (рис. 3.6, а).

где Vn – объем, показанный в разрезе на рис. 3.6, б заштрихованной

площадью abcdea;

2

H

2

H

Vn =

πR2 + πR2

= πR2

R +

.

3

cos α

3

cos α

Следовательно,

2

Pn = ρgπR2

R cos α + H .

3

Сдвигающее усилие Pt направлено параллельно стенке бака и

составляет угол

β = 90◦ − α с вертикалью:

Pt = ρgVt cos β,

где Vt – объем жидкости abca,

представляющий разность объемов

bcfg и abgf для участков полусферы bc и ab

и равный ее объему:

Vt =

2

πR3.

3

Следовательно,

Pt = ρg

2

πR3 sin α.

3

Отметим, что сдвигающая сила не зависит от напора в баке.

Имея две взаимно перпендикулярные составляющие Pn и Pt,

находим полную силу давления, проходящую в данном случае через

центр полусферы:

4

4

P = qPn2 + Pt2 = ρgπR2rH2 +

RH cos α +

R2.

3

9

57

Задачу можно также решить, пользуясь уравнением (3.7), рас-

смотрев равновесие объема жидкости, заполняющей полусферу

(рис. 3.6, в).

Предварительно находим силу N, с которой жидкость, заполня-

ющая бак, действует на плоское сечение ac, и вес G

выделенного

полусферического объема жидкости: N = ρgH πR2

(направлена

по нормали к сечению ac и проходит через его центр давления),

G = ρg

2

πR3 (сила вертикальна и проходит через центр тяжести

полусферического объема).

3

Проектируя найденные силы на направления отрывающего и

сдвигающего усилий, в соответствии с векторным уравнением (3.7)

получаем

2

Pn = N + G cos α = ρgπR2

H +

R cos α ;

3

Pt = G sin α = ρg

2

πR3 sin α.

3

Результирующая сила давления жидкости на погруженное в нее

тело (архимедова сила) направлена вертикально вверх и равна весу

жидкости в объеме V, вытесненном телом:

P = ρgV.

(3.8)

Сила

P проходит через центр тяжести вытесненного объема

жидкости (центр водоизмещения).

При равновесии плавающего тела его центр тяжести и центр во-

доизмещения находятся на общей вертикали (ось плавания).

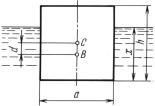
Для устойчивого равновесия тела, плавающего в погруженном

состоянии (подводное плавание), необходимо, чтобы центр тяже-

сти тела

(точка C) лежал ниже центра водоизмещения

(точка B,

рис. 3.7).

плавании тела на поверхности (надводное

плавание,

При

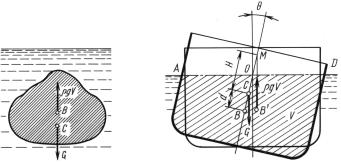
Рис. 3.7

Рис. 3.8

угол θ) метацентр M (точка пересечения линии действия архи-

медовой силы с осью плавания) лежал выше центра тяжести тела C,

т. е. чтобы метацентрическая высота H (расстояние между точками

M и C) была положительна.

Момент устойчивости плавающего тела

Mуст = GH sin θ,

(3.9)

где G – вес тела, равный весу вытесненной жидкости (G = ρgV );

H – метацентрическая высота; θ – угол крена.

При малых углах крена метацентрическую высоту можно опре-

делить по формуле

J

(3.10)

H =

− d,

V

где J – момент инерции площади плавания AD относительно оси

качания O; V – объем тела, погруженного в жидкость; d –

превыше-

ние центра тяжести тела над центром водоизмещения при равнове-

сии. Момент устойчивости плавающего тела

J

Mуст = ρgV (

− d) sin θ.

(3.11)

V

Из формулы (3.11) следует, что для устойчивого равновесия пла-

вающего тела необходимо выполнение условия

J

(3.12)

H =

− d > 0.

V

59

Проверять устойчивость плавающего тела следует относитель-

но той оси, для которой момент инерции площади плавания наи-

меньший.

Пример 2. Деревянный брус ква-

дратного сечения a × a и высотой h, от-

носительная плотность которого δ, пла-

вает в воде (рис. 3.9).

высоту

Определить наибольшую

бруса hmax, при которой плавание еще

Рис. 3.9

будет устойчивым.

Для решения задачи воспользуемся

формулой (3.10),

подставив в нее значение метацентрической вы-

соты H = 0:

J

(3.13)

H =

− d = 0.

V

Погружение бруса x определяется из закона Архимеда:

x = δh.

Определим величины J, V , d,

входящие в формулу (3.10):

a4

J =

; V = a2x = a2 δh;

12

h

x

h

J =

−

=

(1 − δ).

2

2

2

Подставляя найденные значения в формулу (3.13), получаем

a4

−

h

(1 − δ) = 0,

откуда

12a2 δh

2

a

hmax =

.

p

ЗАДАЧИ

6δ(1 − δ)

Задача 3.1. Определить величины и направления сил давления

воды на плоское и полусферическое днища цилиндрического сосу-

да диаметром D = 1 м в трех случаях:

D

D

y = +

; y = −

; y = 0.

60

5

5