715

ческих уравнений, описывающая равновесное состояние, имела ненулевое решение необходимо требовать равенство нулю ее главного определителя (об этом подробнее см. в п. 1.4.1):

33

Раскрыв определитель, получаем соотношение:

Таким образом, если

Р = сl , 3

или

Р = сl ,

при ненулевых значениях отклонений уВ и уС уравнения равновесия будут выполняться. В этом случае рассматриваемая система находится в безразличном состоянии равновесия, а полученные значения сил называются критическими:

Из найденных решений в качестве опасного значения следует выбрать минимальное значение. Рассмотрим теперь формы потери устойчивости. Выделим из системы (3.45)–(3.46) любое уравнение, например первое, и подставим в него минимальное значение критической силы Ркр1:

откуда получаем равенство:

сl (уВ + уС )= 0 . 3

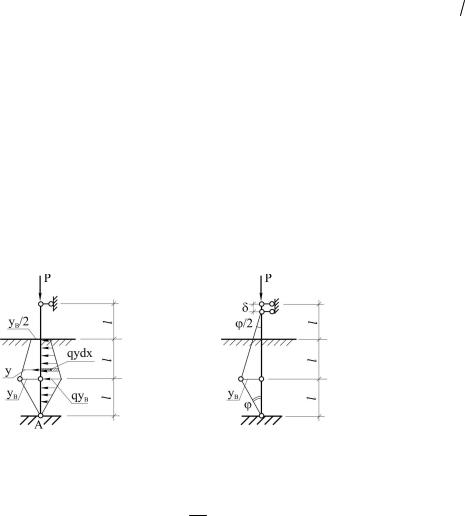
Следовательно при достижении внешней нагрузки значения Ркр1 перемещения шарниров В и С будут равны по величине и противоположны по направлению: уВ = –уС (рис. 3.35). Если далее подставить в уравнение (3.45) значение критической силы Ркр2, то перемещения шарниров В и С будут равны по величине и одинаковы по направлению: уВ = уС (рис. 3.36).

140

Задача 9. Энергетический метод при расчете на устойчивость шарнирно звеньевой системы. На шарнирно звеньевую систему, состоящую из трех одинаковых абсолютно жестких стержней

длиной l, соединенных между собой шарнирами (см. рис. 3.32), действует продольная сила Р. Верхний и нижний шарниры опираются на жесткий фундамент, два средних — на упругие элементы (пружины) жесткостью c.

Определить критическое значение нагрузки энергетическим методом.

Решение.

Идея энергетического метода заключается в том, что исследуется изменение полной потенциальной энергии системы при ее переводе из исходного (невозмущенного) в смежное (возмущенное) состояние. Если это изменение равно нулю, то в исходном состоянии система находится в условиях безразличного состоянии равновесия, а сила, действующая на нее, является критической.

силы (а по сути — груза, установленного на исследуемой системы).

В отличие от статического метода, когда в процессе исследования возмущенного состояния системы перемещения в направлении действия силы считаются малыми второго порядка и по этой причине игнорируются (см. рис. 3.33), энергетический метод исследует изменение потенциала внешней нагрузки. И, следовательно, в этом случае необходимо учитывать перемещение внешней нагрузки в процессе перевода системы из исходного состояния в возмущенное (рис. 3.37).

Рассмотрим изменение упругой энергии системы U. Эта энергия запасается в пружинах. В исходном состоянии пружины находятся в нейтральном положении. Они не сжаты и не растянуты. По этой причине их потенциальная энергия равна нулю. Следовательно, изменение упругой энергии системы равно работе реакций, возникающих в пружинах в процессе перевода системы из

Значительно сложнее определить изменение потенциала внешней нагрузки. Для этого необходимо определить величину δ (см. рис. 3.37). Опускание шарнира D возникает в результате поворотов каждого из трех звеньев, образующих рассматриваемую систему. Рассмотрим первоначально поворот нижнего звена АВ (рис. 3.38). Опускание точки В можно представить в виде:

sin ϕ ϕ , ϕ tgϕ = yB . 2 2 l

Аналогично опускание точки D за счет поворота соответственно верхнего

y2

δ3 = C

2l

и среднего звеньев:

δ2 = (yC − yB )2 . 2l

В итоге полное опускание точки приложения силы Р (точки D) при переводе системы из исходного (недеформированного) в смежное (возмущенное) состояние равно:

141

И, следовательно, изменение потенциальной энергии груза (силы Р) составляет:

В итоге равенство (3.49) с учетом представления (3.50) и (3.51) приобретает вид:

Заметим, что найденное значение силы зависит не только от жесткостных характеристик системы (длины звена l и жесткости пружины c), но и от перемещений шарниров B и C. Каждому значению пары уВ и уС будет соответствовать свое значение силы Р. Очевидно, таких значений

— бесконечное множество, из которого нас будет интересовать самая малая величина. Для ее определения сначала введем замену

t = yC ,

Затем возьмем производную по параметру t и приравняем ее нулю:

Откуда:

2t(t2 − t +1)− (t2 +1)(2t −1)=1− t2 = 0 .

Таким образом, значения параметра t, соответствующие экстремуму функции (3.52), равны:

Это равенство соответствует решению (3.47), полученное статическим методом (при этом уВ = уС, что соответствует форме потери устойчивости, изображенной на рис. 3.35).

Сравните с равенством (3.48).

Задача 10. Статический метод при расчете на устойчивость шарнирно звеньевой системы, помещенной в упругий грунт.

142

Так как справедлива гипотеза Винклера, то очевидно, в возмущенном состоянии система будет нагружена распределенной нагрузкой q = βy по внешнему виду похожей на эпюру перемещений y (рис. 3.41). В дальнейшем распределенную нагрузку заменим равнодействующими силами. Продлим действие нагрузки до точки D, а чтобы не изменился характер действия, введем такую же нагрузку, но обратного направления (пунктирные линии на рис. 3.41). На том же рисунке представлены равнодействующие силы и точки их приложения.

Составим два уравнения равновесия. Первое: сумма моментов всех сил, действующих на си-

Второе уравнение равновесия: сумма моментов всех сил, расположенных ниже врезного шарнира относительно точки В′ (см. рис. 3.41):

Задача 11. Энергетический метод при расчете на устойчивость шарнирно звеньевой системы, помещенной в упругий грунт.

На шарнирно звеньевую систему, состоящую из двух абсолютно жестких стержней и соединенных между собой шарниром, действует сила Р. Верхний и нижний шарниры опираются на жесткий фундамент. Система частично помещена в упругий грунт, подчиняющийся гипотезе Винклера, с коэффициентом постели, равным β . Ее размеры приведены на рис. 3.39.

143

Определить критическое значение нагрузки энергетическим методом.

Решение.

Условие критического состояния представим в виде равенства (3.49). Запишем изменение упругой энергии U упругого основания при переводе системы из исходного состояния в возмущенное. Можно считать, что грунт имеет бесконечный объем, который накопил упругую энергию, равную той работе, которая затрачена на его деформирование. Это деформирование осуществляется силами, равными силам отпора, только направленными в противоположную сторону (см. рис. 3.42). Элементарная сила отпора может быть представлена в виде:

qdx = βydx . Тогда работа, совершенная ими, равна

Здесь учтено, что нагрузка имеет два линейных участка: у1(х) — это перемещения точек нижнего звена системы; у2(х) — это перемещения точек верхнего звена системы. Запишем уравнение пере-

Изменение потенциальной энергии груза запишем аналогично тому, как это сделано в задаче 9.

Если учесть, что

ϕ tgϕ = yB , l

то перемещение силы Р можно окончательно представить как

144

δ= 3 уВ2 . 4 l

Тогда изменение потенциальной энергии груза запишем в виде:

3 у2 П = −δР = − В Р . (3.55)

4l

Сучетом соотношений (3.54) и (3.55), условие (3.49) дает значение критической силы:

Такой же результат был получен статическим методом (см. равенство (3.53)). Задача 12. Устойчивость стойки, состоящей из упругой и абсолютно жесткой частей.

Консольно защемленная стойка состоит из двух частей одинаковой длины l . Нижняя часть упругая, имеет изгибную жесткость EJ. Верхняя часть — абсолютно жесткая. Стойка нагружена продольной силой, как это показано на рис. 3.44.

Определить критическое значение нагрузки статическим методом.

Решение.

Прежде чем решать задачу, оценим диапазон, внутри которого должно находиться искомое значение критической силы. Очевидно, верхняя граница критической силы может быть определена, если сила Р будет приложена на границе упругой и абсолютно жесткой частей стойки (рис. 3.45). Нижняя граница может быть определена из предположения, что по всей своей длине стойка — упругая (рис. 3.46). Используя известные формулы сопротивления материалов, определяем диапазон, внутри которого находится искомое значение критической силы:

Исходя из этих посылок, можно грубо оценить величину критической силы, равной середине обозначенного диапазона:

Точное решение задачи. На рис. 3.47 представлено возмущенное состояние стойки. Так как ее нижний участок имеет бесконечное число степеней свободы, система уравнений равновесия вырождается в одно дифференциальное уравнение:

145

Это уравнение относится к классу неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. Его общее решение состоит из двух слагаемых. Первое — общее решение однородного дифференциального уравнения:

у(x) = Asin(nx)+ Bcos(nx).

Второе — частное решение неоднородного дифференциального уравнения:

Реализуем эти условия, начиная с третьего. Прежде запишем производную от решения (3.61): y′(x)= Ancos(nx)− Bnsin(nx).

Тогда третье граничное условие имеет вид:

Anl cos(nl)− Bnlsin(nl)= δ − Asin(nl)− Bcos(nl)− δ .

В итоге, система граничных условий вырождается в систему линейных однородных уравнений:

A 0 + B 1+ δ 1 = 0

+ + δ =

A n B 0 0 0

A(nl cosnl + sin nl)+ B(− nlsin nl + cosnl)+ δ 0 = 0.

Ненулевое решение этой системы возможно, если ее главный определитель равен нулю:

Раскрыв этот определитель, получаем уравнение критического состояния: n(− nlsin nl + cosnl)= 0 ,

или

146

Полученное уравнение относится к классу трансцендентных, решение которых в явном виде невозможно. Чтобы получить результат, воспользуемся методом Ньютона. Для этого введем замену:

и перепишем уравнение (3.62) в виде:

F(t)= t − ctg(t)= 0 .

Метод Ньютона решения нелинейных уравнений — это циклический процесс, при котором каждое последующее приближении, основанное на предыдущем решении, все ближе к истинному результату:

ti+1 = ti − F′((ti )). F ti

где i — номер приближения.

Процесс останавливается, когда разность двух соседних приближений меньше наперед заданного сколь угодно малого значения. Запишем первую производную функции F(t):

Таким образом, формула Ньютона в нашем случае приобретает вид:

ti+1 = ti − t − ctg(t(i )). 2 + ctg2 ti

В качестве начального приближения возьмем значение t1 = π =1,5708 . Ниже приведен расчет, 2

из которого видно, что результат с точностью до четвертого знака после запятой начинает повторяться уже после третьего приближения:

t2 = 1,5708 − 1,5708 − 0 = 0,7854, 2 + 0

t3 = 0,7854 − 0,7854 −1 = 0,8569. 2 +1

t4 = 0,8569 − 0,8569 − 0,8663 = 0,8603. 2 + 0,7505

t5 = 0,8603 − 0,8603 − 0,8604 = 0,8603. 2 + 0,7403

Таким образом, полученное решение

t= nl = 0,86

сучетом равенства (3.59) дает значение критической силы:

(nl)2 = P l2 = 0,74

EJ

или

EJ

Ркр = 0,74 . (3.64) l2

Заметим, что полученное точное значение силы находится в установленном диапазоне (см. условие (3.57)), однако существенно отличается от предполагаемого значения (3.58).

Задача 13. Устойчивость рамы, нагруженной однопараметрической системой сил.

147

На раму, изображенную на рис. 3.48, действует однопараметрическая система сжимающих сил. Изгибная жесткость ригеля в два раза больше изгибной жесткости стоек. Линейные размеры рамы приведены на рис. 3.48.

Определить значение критической нагрузки.

Решение.

Задачу будем решать методом перемещений. Но прежде выполним приведение жесткостей элементов рамы и параметров сжимающей силы. Для этого заполним таблицу 3.1. Первая часть таблицы — приведение жесткостей — выполняется по обычной процедуре, принятой в классической строительной механике. Вторая часть таблицы — приведение параметров сжимающей силы — вы-

полняется аналогично приведению жесткостей. Первоначально для каждого стержня вычисляется свой параметр сжимающей силы из формулы (2.29)

N :

EJ

Затем один из этих параметров (в нашем случае для стержня АВ) обозначается как параметр v0:

криволинейны. Ригель ВС не сжимается, и по этой причине на этом элементе эпюра строится так, как это принято в классической строительной механике. Запишем

канонические уравнения метода перемещений (см. п. 2.4.3) для рассматриваемого случая:

148

R1P = r11(P)z1 + r12 (P)z2 = 0,

R2P = r21(P)z1 + r22 (P)z2 = 0.

Ненулевое решение этой системы возможно, если ее главный определитель равен нулю:

r11(P) r12 (P) = 0 . r21(P) r22 (P)

Раскрыв определитель, получаем характеристическое уравнение

Для нахождения коэффициентов следует рассмотреть равновесие узлов В и С.

С учетом этих значений равенство (3.66) приобретает вид: [12i0 + 6i0ϕ2 (v0 )][12i0 + 3i0ϕ1(1,06v0 )]− 36i02 = 0

или

ϕ1(1,06v0 )ϕ2 (v0 )+ 2ϕ1(1,06v0 )+ 4ϕ2 (v0 )+ 6 = 0.

Таким образом, получено уравнение, в котором неизвестным является значение v0. Для его решения левую часть уравнения будем рассматривать как некоторую функцию от параметра v0:

F(v0 )= ϕ1(1,06v0 )ϕ2 (v0 )+ 2ϕ1(1,06v0 )+ 4ϕ2 (v0 )+ 6 = 0. (3.67)

Требуется найти минимальное значение аргумента этой функции, при котором она обращается в ноль. Прежде определим диапазон, внутри которого находится искомое решение. Для этого ослабим систему. В узлы В и С врежем шарниры (см. рис. 3.52) и тем самым определим минимальную величину v0. Затем усилим раму: в те же узлы установим плавающие заделки (рис. 3.53) и найдем максимальное значение v0. В результате система упрощается, ее расчет сводится к анализу одиночных стержней, известному из курса сопротивления материалов.

149