
715
.pdf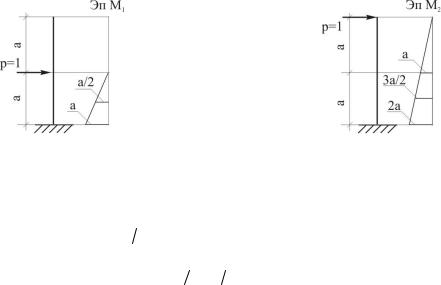
5. Несмотря на то, что при = f система мгновенно изменяема (три шарнира находятся на одной
прямой), усилия в стержнях конечны. Действительно, в этом случае деформации ограничены, а значит, ограничены и продольные силы (см. равенство (2.121)).
ГЛАВА 3. ПРИМЕРЫ РЕШЕНИЙ ЗАДАЧ
3.1.Динамика сооружений
3.1.1.Свободные колебания
Задача 1. Свободные колебания жестко защемленной консольной стойки с двумя одинаковыми массами.
На невесомой консольно защемленной балке с равным шагом расположены два одинаковых груза (рис. 3.1). Известны жесткость балки EJ, масса груза m, длина стойки 2а.
Определить частоты и формы свободных колебаний.
Решение.
Система имеет две степени свободы. Нижней массе присвоим индекс 1, верхней — индекс 2. Для данной системы запишем систему линейных однородных уравнений (1.36) в виде:
(δ11m1 − λ)v1 + δ12m2v2 = 0 |
|
|||||||||
δ |
21 |
m v + (δ |
22 |
m |
2 |
− λ)v |
2 |
= 0. |
(3.1) |
|
|
1 |
1 |
|
|
|
|
||||
Коэффициенты δij в системе уравнений (3.1) имеют тот же смысл, что и в классической строительной механике, и определяются по известному алгоритму:
–по направлению возможных перемещений масс последовательно прикладываются единичные нагрузки;
–строятся эпюры изгибающих моментов;
–эпюры последовательно сопрягаются.
Реализуем этот алгоритм. На рис. 3.2 и 3.3 представлено нагружение конструкции единичными нагрузками и эпюры изгибающих моментов от этих загружений.
Рис. 3.2. Нагружение стойки |
Рис. 3.3. Нагружение стойки |
единичной силой по первому |
единичной силой по второму |
направлению |
направлению |
Определим коэффициенты системы уравнений (3.1).
δ11 |
= {М1 |
× М1}= |
|
а |
[а2 + 4(а 2)2 ]= |
2а3 |
, |
|
|
|
||||||||||||
|
|
6EJ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
6EJ |
|
|
|
|
|
|
|
||||||
δ |
|
= δ |
|
= {М |
|
|
× М |
|
}= |
|
а |
[а 2а + 4(а 2)(3а 2)]= |
5а3 |
, (3.2) |
||||||||
|
21 |
1 |
2 |
|
|
|
||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
6EJ |
|
|
|
|
|
6EJ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
δ |
|
= {М |
|
× М |
|
}= |
2а |
[(2а)2 + 4(а)2 ]= |
16а3 |
. |
|
|||||||||||
22 |
2 |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
6EJ |
|
|
|
|
6EJ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ненулевое решение системы уравнений (3.1) возможно, если ее главный определитель будет
равен нулю: |
|
|
|
|
|
|
|
|
|
|
|
= |
|
(δ11m − λ) |
|
δ12m |
|
= 0. |
|
||||
|
|
|
|
||||||||
|
δ |
21 |
m (δ |
22 |
m − λ) |
|
|
||||
Введя замену |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = |
ma3 |
, |
|
|
(3.3) |
||
|
|
|
|
6EJ |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
120

с учетом соотношений (3.2) перепишем определитель в виде:
= |
|
(2t − λ) |
5t |
|
= 0 . |
|
|
||||
|
5t |
(16t − λ) |
|
Раскрыв определитель, получаем квадратное уравнение относительно параметра λ:
λ2 −18λt + 7t2 = 0.
Решаем его:
λ1 2 = 9t ± |
(9t)2 − 7t2 |
= 9t ± 8,60t . |
|
Таким образом: |
|
||
λ1 = 17,60t, |
(3.4) |
||
|
λ2 = 0,40t. |
(3.5) |
|
С учетом равенств (3.3)–(3.5) из соотношения (1.40) вычисляем частоты свободных колебаний:
ω = |
|
1 |
|
|
|
= |
|
1 |
|
|
= 0,584 |
|
|
EJ |
, |
(3.6) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
λ |
|
|
|
|
|
17,60t |
|
|
|
ma3 |
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ω |
|
= |
1 |
|
|
= |
1 |
|
|
= 3,88 |
|
EJ |
. |
(3.7) |
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
λ |
|
|
|
|
0,40t |
|
|
ma3 |
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим теперь формы свободных колебаний. Для этого исключим из системы (3.1) второе уравнение.
Первая форма колебаний.
Примем в качестве амплитудного значения перемещения по первой форме колебаний: v1(1) =1. В итоге первое уравнение системы (3.1) с учетом представлений (3.2) и (3.3) принимает вид:
(2t − λ1 ) 1+ 5tv2(1) = 0 .
Если в это уравнение подставить условие (3.4), то перемещение второй массы по первой форме колебаний составляет:
v2(1) = − 2t −17,60t = 3,12 . 5t
Таким образом, пара чисел v1(1) = 1 и v2(1) = 3,12 определяют первую форму собственных коле-
баний стойки с частотой ω1 (см. равенство (3.6)).
Вторая форма колебаний.
Поступаем аналогично. Для начала, положим, что перемещение первой массы по второй формы колебаний равно единице: v1(2) =1. С учетом этого, первое уравнение системы (3.1) принимает вид:
(2t − λ2 ) 1+ 5tv2(2) = 0 . Подставим в него представление (3.5) и получаем:
v2(2) = − 2t − 0,40t = −0,32 . 5t
В итоге пара чисел v1(2) = 1 и v2(2) = −0,32 определяют вторую форму собственных колебаний
стойки с частотой ω2 (см. равенство (3.7)).
На рисунках (3.4) и (3.5) представлены эти формы колебаний. При построении форм изгиба учтено, что положительное направление перемещений совпадают с соответствующим направлением действия единичных нагрузок (см. рис. 3.2 и 3.3).
121
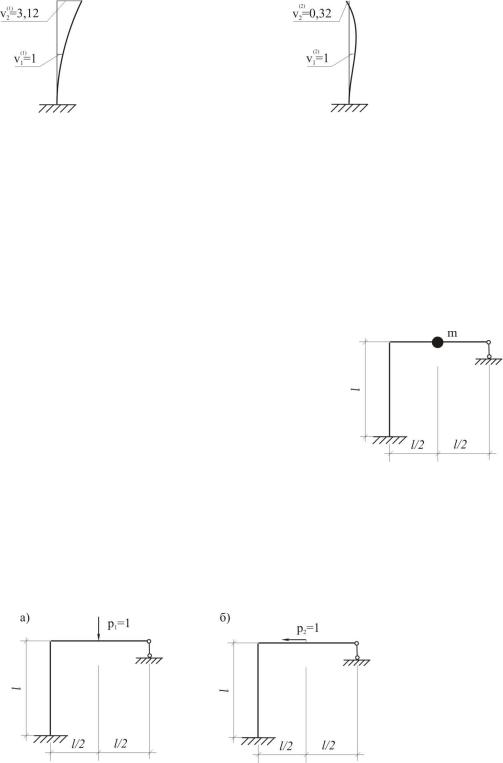
Рис. 3.4. Колебания стойки по первой форме с часто- |
Рис. 3.5. Колебания стойки по второй форме с часто- |
той ω1 |
той ω2 |
Проверка ортогональности.
Если правильно определены формы колебаний, то должно выполняться условие (1.42). В нашем случае:
∑2 [ (k) ( j) ]= (1) (2) + (1) (2) =
mivi vi m1v1 v1 m2v2 v2
i=1
= m 1 1+ m 3,12 (− 0,32)= m(1− 0,9984)= 0,0016.
Это означает, что проверка сошлась с точностью 0,16 %.
Задача 2. Свободные колебания Г-образной статически неопределимой рамы с двумя степенями свободы.
На ригеле Г-образной невесомой рамы (рис. 3.6) установлен груз массой m. Длины стойки и ригеля одинаковы и равны l . Изгибная жесткость ригеля в два раза больше изгибной жесткости стойки: EJp =
2EJc.
Определить частоты и формы свободных колебаний.
Решение
Система имеет две степени свободы: масса имеет возможность перемещаться как в вертикальном, так и в горизонтальном направлениях. По этой причине система уравнений, описывающая свободные колебания рамы имеет вид (3.1). Ненулевое решение этого уравнения возможно, если ее главный определитель равен нулю:
Рис. 3.6. Расчетная схема рамы, имеющей
две степени свободы
= |
|
(δ11m − λ) |
|
δ12m |
|
= 0. |
(3.8) |
|||
|
|
|
||||||||
|
δ |
21 |
m |
(δ |
22 |
m − λ) |
|
|||
|
|
|
|
|
|
|
|
|
||
Для определения коэффициентов δij в условии (3.8) необходимо последовательно загрузить раму единичными силами по направлениям возможных перемещений массы (рис. 3.7).
Рис. 3.7. Нагружение рамы единичными нагрузками по первому (а) и второму (б) направлениям
После чего необходимо построить эпюры изгибающих моментов от каждого из этих загружений. Однако исходная рама является один раз статически неопределимой. По этой причине всякий раз, прежде чем строить соответствующие единичные эпюры, необходимо раскрывать статическую неопределимость.
Первое загружение.
Отбросим правую шарнирную опору и заменим ее действие неизвестной реакцией Х1. Получили основную систему, изображенную на рис. 3.8.
122
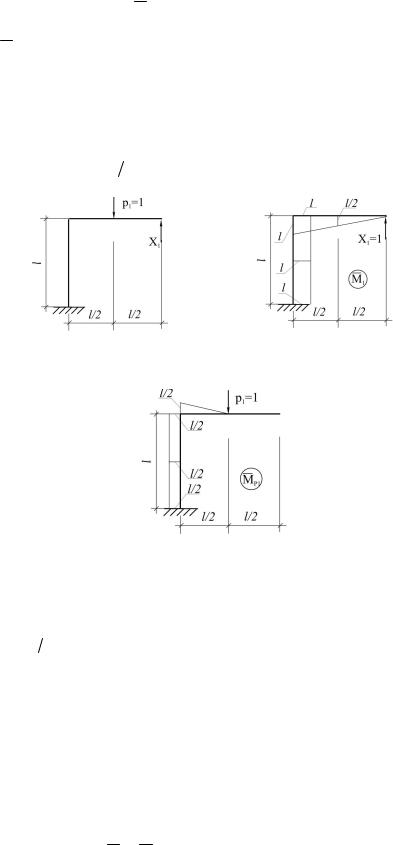
Дальнейшая процедура известна из курса классической строительной механики. По направлению отброшенной связи в основной системе направим единичную силу Х1 = 1, от действия которой стро-
им эпюру изгибающих моментов М1 (рис. 3.9). Затем основную систему загружаем внешней нагрузкой, которой в рассматриваемом случае является сила р1 = 1. И вновь строим эпюру изгибаю-
щих моментов МР1 (рис. 3.10). Запишем теперь каноническое уравнение метода сил:
|
|
|
|
|
|
|
|
|
δ |
11 Х1 + |
|
1Р = 0 . |
(3.9) |
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= { |
|
|
|
|
× |
|
|
|
}= |
l |
|
[l2 + 4l2 + l2 |
]+ |
|||||
|
δ |
M |
1 |
M |
||||||||||||||||
|
|
|
|
|||||||||||||||||
11 |
|
|
|
1 |
|
6EJс |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ |
|
|
|
l |
|
|
[l2 + 4(l 2)2 ]= |
7l3 |
. |
(3.10) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
6EJр |
|
|
|
|
|
6EJc |
|
|||||||||
Рис. 3.8. Основная система |
Рис. 3.9. Эпюра изгибающих моментов |
метода сил по первому загружению |
от единичной силы, направленной |
|
по направлению отброшенной связи |
Рис. 3.10. Эпюра изгибающих моментов от единичной силы, направленной по первому направлению
|
|
|
|
|
|
|
|
l |
|
l2 |
l2 |
l2 |
|
|
|||
|
|
= {M1 |
|
|
Р1}= − |
|
|||||||||||
1Р |
× M |
|
|
|
|
+ 4 |
|
+ |
|
|
− |
||||||
6EJ |
|
2 |
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
с |
|
|
|
|
|||||
|
l |
2 |
l2 |
|
|
|
l |
|
l |
|
|
|
|
l3 |
|
|
|
|||||
− |
|
|
|
|
+ |
4 |
|
|
3 |
|
= − |
53 |
. |
(3.11) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
6EJр 2 |
|
|
4 4 |
|
|
|
96EJс |
|
|
|
|||||||||||
В этом случае равенство (3.9) приобретает вид: |
|
|||||||||||||||||||||
|
|
|
7l3 |
X |
|
− |
53l3 |
|
= 0. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
6EJс |
|
|
|
96EJс |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
= |
53 |
= 0,473. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
112 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теперь строим окончательную эпюру изгибающих моментов от первого загружения рамы
(рис. 3.11): |
|
M1 = X1M1 + MP1 , |
(3.12) |
123
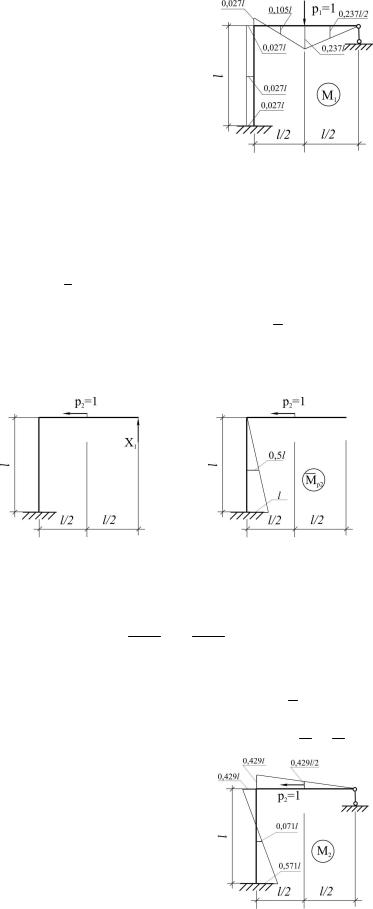
Рис. 3.11. Эпюра изгибающих моментов в раме от первого загружения
Второе загружение.
В качестве основной системы в этом случае целесообразно выбрать ту же схему, что и при первом загружении (см. рис. 3.12). Такой выбор основной системы несколько упрощает процедуру решения, так как эпюра изгибающих моментов от действия единичной нагрузки, действующей по направлению отброшенной связи, уже построена (см. рис. 3.9). Тем самым известно значение коэффициента δ11 (см. равенство (3.10)).
Грузовую эпюру строим от единичной силы, направленной по второму направлению (рис. 3.13).
После чего определим величину коэффициента |
|
1Р : |
|
||||||||||||||||
|
|
|
= { |
|
|
|
× |
|
|
}= |
l |
l2 |
+ 4l |
l |
|
= |
3l3 |
. |
(3.13) |
|
|
|
M |
|
|
M |
|
||||||||||||
|
1Р |
1 |
Р2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6EJc |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
6EJc |
2 |
|
|
|
||||
Рис. 3.12. Основная система |
Рис. 3.13. Эпюра изгибающих |
|
моментов от единичной силы, |
||
метода сил по второму загружению |
||
направленной по второму направлению |
Тогда каноническое уравнение метода сил (3.9) приобретает вид:
7l3 X1 + 3l3 = 0 . 6EJc 6EJc
Откуда реакция шарнирной опоры равна
Х1 = − 3 = −0,429 . 7
Тогда эпюра изгибающих моментов от второго загружения примет вид (рис. 3.14)
M2 = X1M1 + MP2 ,
Рис. 3.14. Эпюра изгибающих моментов в раме от второго загружения
124

Теперь можно определить коэффициенты, входящие в равенство (3.8).
δ11 = {M1 × M1}= {M1 × MP1}=
= |
|
l |
|
|
[0,027l 0 5l + 4 0,027l 0 5l + 0,027l 0 5l]+ |
|
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
6EJc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
0 5l |
[0,027l 0 5l − 4 0,105l 0,25l]= 0,0097 |
|
l3 |
. |
(3.14) |
|||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
6EJр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJс |
|
||||||||
δ12 = δ21 = {М1 × М2}= {М1 × |
|
Р2}= {М2 × |
|
Р1}= |
|
||||||||||||||||||||||
М |
М |
|
|||||||||||||||||||||||||
= − |
|
l |
[0,027l l + 4 0,027l 0 5l]= −0,0133 |
l3 |
. |
(3.15) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
6EJс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJс |
|
||||||
|
|
|
|
|
|
|
|
δ22 = {М2 × М2}= {М2 × |
|
|
|
Р2}= |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
М |
|
|
|
|
|
|
|
|
|||||||||||
= |
|
|
l |
[0,571l l + 4 0,071l 0 5l]= 0,1188 |
|
l3 |
. |
(3.16) |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
6EJс |
|
|
|
|
|
|
|
|
|
|
|
|
|
EJс |
|
||||||||
Теперь можно записать условие (3.9) в виде: |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
(0,97t − λ) |
−1,33t |
|
= 0 . |
|
|
|
|
|
|
|
(3.17) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
−1,33t |
(11,88t − λ) |
|
|
|
|
|
|
|
|
|||||||||
Здесь обозначено: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
t = 0,01 |
ml3 |
. |
|
|
|
|
|
|
|
(3.18) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
EJс |
|
|
|
|
|
|
|
|
||||||||
Раскрыв определитель (3.17), получаем квадратное уравнение относительно параметра λ (0,097t − λ)(11,55t − λ)− (1,33t)2 = 0,
λ2 −12,85tλ + 9,75t2 = 0. |
|
Решив которое, получаем: |
|
λ1 = 12,04t, |
(3.19) |
λ2 = 0,81t. |
(3.20) |
С учетом представления (1.40), собственные частоты колебаний соответственно по первой и второй формам колебаний равны:
ω = |
1 |
|
|
|
= |
|
1 |
|
|
= 2,88 |
|
|
EJс |
, |
(3.21) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
λ |
|
|
|
|
|
|
12,04t |
|
|
|
ml3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ω |
|
= |
1 |
|
|
|
|
= |
1 |
|
|
= 11,11 |
|
|
EJс |
. |
(3.22) |
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
0,81t |
|
|
|
ml3 |
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определение форм колебаний.
Исключим из системы уравнений (3.1) второе уравнение. В первое уравнение подставим значения коэффициентов (3.14) и (3.15):
|
|
l3 |
|
|
|
l3 |
|
|
|
0,0097 |
|
m − λ v |
+ −0,0133 |
|
|
mv = 0 . |
|
|
|
|
||||||
|
|
EJс |
|
1 |
|
EJ |
2 |
|
|
|
|
|
|
с |
|||
Тогда это уравнение с учетом представления (3.18) запишется в виде:
(0,97t − λ)v1 + −1,33tv2 = 0. |
(3.23) |
Первая форма колебаний.
Примем v1(1) =1; и (см. равенство (3.19)) λ = λ1 = 12,04t. С учетом этих представлений уравнение (3.23) дает значение
125
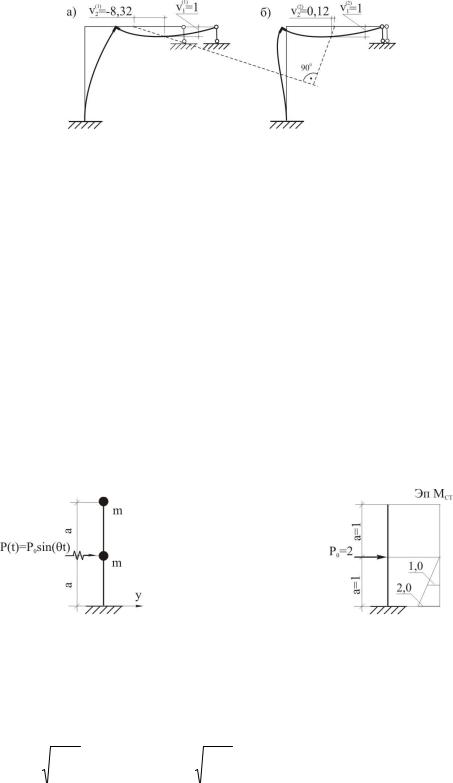
v2(1) = −8,32 .
Вторая форма колебаний.
Примем v1(2) =1; и (см. равенство (3.20)) λ = λ2 = 0,81t. В этом случае уравнение (3.23) дает значение
v2(2) = 0,12 .
На рис. 3.15, а и рис. 3.15, б соответственно представлены формы свободных колебаний с частотой ω1 и ω2. Здесь пунктиром отмечены вектора полного перемещения масс по первой (v(1)) и второй (v(2)) формам колебаний. Заметим, что в этом частном случае они пересекаются под углом 90˚.
Рис. 3.15. Первая (а) и вторая (б) формы колебаний рамы
Проверка ортогональности.
∑2 [mivi(k)vi( j) ]= m1v1(1)v1(2) + m2v2(1)v2(2) =
i=1
=m 1 1+ m (− 8,32) (0,12)= m(1− 0,9984)= 0,0016.
3.1.2 Вынужденные колебания
Задача 3. Вынужденные колебания жестко защемленной консольной стойки с двумя одинаковыми массами.
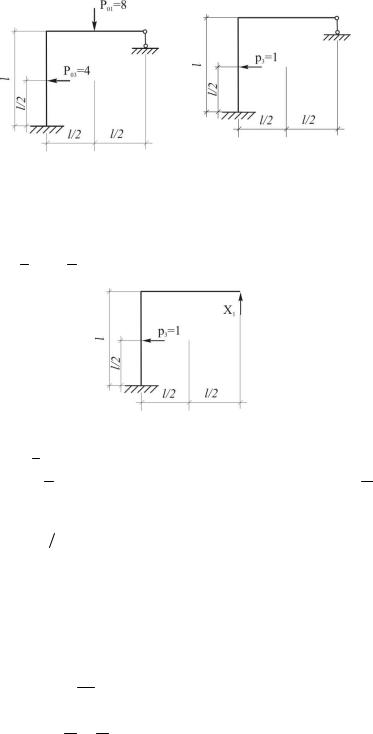
На невесомой консольно защемленной балке с равным шагом расположены два одинаковых груза (рис. 3.16). На нижний груз в горизонтальном направлении действует возмущающая сила P(t)= 2sin(0 5t) . Принять: EJ = 1, m = 1, a = 1.
Требуется построить эпюру изгибающих моментов только от действия возмущающих сил (статическую эпюру изгибающих моментов) и эпюру изгибающих моментов от действия возмущающих сил и сил инерции (динамическую эпюру изгибающих моментов).
Решение
Для построения статической эпюры достаточно на исходную балку приложить амплитудные значения всех возмущающих сил (в данном случае силу Р0 = 2), действующих на исходную систему (см. рис. 3.17). На том же рисунке представлена статическая эпюра изгибающих моментов.
Рис. 3.16. Консольно защемленная балка, нагруженная
Рис. 3.17. Статическая эпюра
возмущающей силой
изгибающих моментов
При построении динамической эпюры изгибающих моментов необходимо определить максимальные значения сил инерции, возникающих в процессе вынужденных колебаний. Для этого нужно вычислить амплитудные значения перемещений масс (v1 и v2). Ранее (см. задачу 1), для данной системы были определены собственные частоты колебаний, которые с учетом условий данной задачи равны:
ω = 0,584 |
EJ |
= 0,584 ; ω |
|
= 3,88 |
EJ |
= 3,88 . |
|
2 |
|
||||
1 |
ma3 |
|
|
ma3 |
|
|
|
|
|
|
|
126
Под действием возмущающей нагрузки стойка будет испытывать колебания с частотой возмущающей силы Р(t) равной θ = 0 5 рад/с . Амплитудные значения этих колебаний (v1 и v2) определим из
системы линейных алгебраических уравнений (1.47):
(δ m − λ |
θ |
)v + δ m v + |
1P |
= 0; |
||||||||||
|
11 1 |
|
1 |
12 |
2 |
2 |
|
|
θ |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ m v + (δ |
22 |
m − λ |
θ |
)v |
2 |
+ |
|
2P |
= 0. |
|||||
|
21 1θ 1 |
|
|
2 |
|
|
|
|
θ |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь (см. равенство (1.46)):
λθ = |
1 |
= |
1 |
= 4. |
|
θ2 |
0 52 |
||||
|
|
|
(3.24)
(3.25)
Заметим также, что коэффициенты δij (i = 1,2; j = 1,2) имеют смысл перемещений по i-му
направлению от единичной силы, действующей по j-му направлению. Эти коэффициенты определены ранее в задаче 1 (см. равенства (3.2)), и для исходных значений этой задачи равны:
δ |
= |
2а3 |
= |
1 |
, |
δ = δ |
|
= |
5а3 |
= |
5 |
, δ |
|
= |
16а3 |
= |
8 |
. (3.26) |
|
|
|
|
|
|
|
|
|||||||||||
11 |
|
6EJ |
3 |
|
12 |
21 |
|
6EJ |
6 |
|
22 |
|
6EJ |
3 |
|
|||
Физический смысл свободных членов в системе (3.24) ( |
iP (i = |
|||||||||||||||||
= 1,2)) — это перемещения по i-му направлению от амплитудного значения всех возмущающих сил (в данном случае силы Р0 = 2), действующих на рассматриваемую систему. Поэтому для их вычисления необходимо произвести сопряжения соответствующих единичных (см. рис. 3.2, 3.3) эпюр на эпюру Мст (рис. 3.17):
|
= {М1 × Мст}= |
1 |
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|||||||||
1р |
|
|
|
|
1 |
|
2 + 4 |
|
|
|
1 |
= |
|
|
|
, |
|
||||||
6 |
1 |
|
|
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.27) |
|||
|
= {М2 |
|
|
}= |
|
|
1 |
|
|
|
|
|
3 |
|
|
|
10 |
|
|||||
2р |
× М |
ст |
|
|
|
|
|
2 |
2 + 4 |
|
|
1 |
= |
|
|
. |
|||||||
|
|
|
|
|
2 |
6 |
|||||||||||||||||
|
|
|
|
|
|
6 1 |
|
|
|
|
|
|
|
|
|||||||||
Теперь система линейных уравнений (3.24) с учетом значений (3.25)–(3.27) приобретает вид:
|
1 |
|
|
|
|
|
5 |
|
|
|
|
2 |
|
||||
|
1 |
− |
+ |
1 |
v2 |
+ |
= 0; |
||||||||||
|
|
|
4 v1 |
|
|
||||||||||||
3 |
6 |
3 0,25 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
5 |
|
|
|
|
8 |
|
|
|
|
|
|
10 |
|
||||
|
|
|
1 |
v |
+ |
|
1− 4 v |
|
+ |
|
= 0. |
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
3 |
|
|
|
|
2 |
|
6 0,25 |
|
|||
6 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Эта система сводится к виду:
− 22v1 + 5v2 |
+16 = 0 |
|||
|
−10v2 |
+ |
40 = |
, |
5v1 |
0 |
|||
решение которой определяет амплитудные значения вынужденных колебаний системы:
v1 = 1,84; v2 = 4,90.
С учетом этого максимальные значения сил инерции (см. равенство (1.48)) составляют:
I1 = m1v1θ2 = 1 1,84 0 52 = 0,46;
I2 = m2v2θ2 = 1 4,90 0 52 = 1,22.
127

Силы инерции по знаку — положительны, по этой причине направление их действия совпадает с направлением единичных нагрузок на рис. 3.2 и 3.3. Таким образом, в самый неблагоприятный момент, когда колеблющиеся массы находятся в амплитудном положении, на стойку слева направо действует три силы: кроме амплитудного значения возмущающей силы Р0 = 2 еще и силы инерции I1 = 0,46 и I2 = 1,22 (см. рис. 3.18). На том же рисунке также представлена эпюра изгибающих моментов от совместного действия этих сил: динамическая эпюра. Заметим, что при учете сил инерции максимальное значение изгибающего момента в конструкции примерно в 2,5 раза больше (сравните эпюры на рис. 3.17 и 3.18) чем без их учета.
Задача 4. Вынужденные колебания Г-образной статически неопределимой рамы с двумя степенями свободы.
На ригеле Г-образной невесомой рамы (рис. 3.19) установлен груз массой m. Длины стойки и ригеля одинаковы и равны l . Изгибная жесткость ригеля в два раза больше изгибной жесткости стойки: EJp = 2EJc. На раму действуют две возмущающие силы P1(t) и P3(t), как это показано на рис. 3.19.
Дано: EJс = 1, m = 1, l =1, P1(t)= 8sin 2t , P3 (t)= 4sin 2t . Требуется построить статическую и динамическую эпюры изги-
бающих моментов.
Решение.
Рис. 3.18. Динамическая эпюра изгибающих моментов в стойке
Рис. 3.19. Рама, нагруженная системой возмущающих сил
При решении задач, в которых на строительную конструкцию действует система возмущающих сил, приходится вводить некоторые ограничения на параметры
этих нагрузок. В этом случае, с одной стороны, сужается класс решаемых задач, а с другой — значительно упрощается процесс решения, в основе которого лежат обычные процедуры классической строительной механики. Рассмотрим подробнее эти ограничения.
Первое. Система возмущающих сил — синхронна. Это означает, что все возмущающие силы изменяются с одной частотой. Природа возмущающих сил (см. пп. 1.1.1 и 1.3) состоит в возникновении центробежных сил при работе электродвигателя, используемого в механизмах, установленных на строительных конструкциях. Если паспортная частота всех электродвигателей одинакова, то это требование будет выполняться.
Второе. Система возмущающих сил — синфазна. Это возможно, если эти силы синхронны и включены таким образом, что все возмущающие силы в указанных направлениях (в рассматриваемой задаче для силы P1(t) — это вертикальное, а для силы P3(t) — горизонтальное направления) достигают максимального значения в один момент времени. Заметим, что в этом случае в тот же момент времени максимального значения будут достигать и все силы инерции. Требование синфазности в реальной конструкции за все время эксплуатации может быть никогда и не выполнено. Однако, анализируя самый неблагоприятный вариант нагружения сооружения, можно предположить, что когда-нибудь возможна и такая ситуация.
Третье. Вынужденные колебания не должны происходить в резонансном режиме. Это требование продиктовано двумя обстоятельствами. Во-первых, в большинстве случаев строительные сооружения обладают большой жесткостью, и по этой причине существует абсолютный запрет их эксплуатации в резонансной зоне. Для машиностроительных конструкций это требование не столь категорично, однако, и это — второе обстоятельство, если частоты свободных и вынужденных колебаний совпадают, то в процессе решения задачи необходимо учитывать силы трения, которыми обычно пренебрегают.
Заметим, что для этой рамы частоты свободных колебаний найдены в задаче 2. Используя исходные данные задачи 4, определяем (см. равенства (3.21) и (3.22)) величины собственных частот:
ω = 2,88 |
EJС |
= 2,88, |
|||||
|
|||||||
|
1 |
|
|
ml3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
=11,11 |
|
EJС |
|
=11,11. |
|
2 |
ml3 |
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
128
Тем самым подтверждается, что частоты вынужденных колебаний (по условию задачи θ = 2) находятся вне резонансной зоны.
Статическая эпюра изгибающих моментов.
Чтобы построить статическую эпюру необходимо заданную один раз статически неопределимую раму загрузить амплитудными значениями возмущающих нагрузок, как это показано на рис. 3.20. И от действия этих сил построить эпюру изгибающих моментов. Прежде чем это делать, в дополнение к двум ранее проведенным загружениям единичными нагрузками по первому и второму направлениям (см. задачу 2), выполним еще один расчет: построим эпюру изгибающих моментов от действия единичной нагрузки, действующей по направлению силы Р03 (см. рис. 3.21).
Рис. 3.20. Расчетная схема рамы,
Рис. 3.21. Расчетная схема рамы,
нагруженная статической нагрузкой
нагруженная единичной силой по третьему направлению
Вновь выберем основную систему в том виде, как это сделано в задаче 2, отбросив шарнирную опору (см. рис. 3.22). Каноническое уравнение метода сил имеет вид:
δ11 Х1 + 1Р = 0 .
Рис. 3.22. Основная система метода сил по третьему загружению
При этом коэффициент δ11 известен и определен в задаче 2 (см. равенство (3.10)). Чтобы найти
значение свободного члена |
1Р необходимо произвести сопряжение эпюры М1 (см. рис. 3.9) и |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
грузовой эпюры МР3 , построенной на рис. 3.23. |
|||||||||||||||||||||
|
|
|
= { |
|
|
|
× |
|
|
}= |
l 2 |
l |
l |
+ 4l |
l |
|
= |
3l3 |
. |
||
|
1Р |
M |
1 |
M |
Р3 |
||||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24EJc |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6EJc |
2 |
|
4 |
|
||||
Тогда каноническое уравнение метода сил имеет вид:
7l3 |
X |
|
+ |
3l3 |
= 0 . |
|
6EJc |
1 |
24EJc |
||||
|
|
|
||||
|
|
|
|
Реакция в шарнирной опоре равна:
Х1 = − 3 . 28
Строим окончательную эпюру, используя равенство
M3 = X1M1 + MP3 .
Эта эпюра представлена на рис. 3.24.
129
