презентация_Л2-3

При записи задачи ЛП в канонической форме число линейно независимых уравнений, как правило, намного меньше числа переменных.

Если число независимых уравнений больше числа переменных, то такая система несовместна (нет решений)

Если число независимых уравнений равно числу переменных, то система имеет единственное решение (недопустимое, если хотя бы одна из его компонент < 0, либо искомое оптимальное)

Пусть

m – число линейно независимых уравнений, n m – число переменных

Тогда при совместимости системы у нее существует бесконечное множество решений.

Вэтих решениях

n m свободных переменных (могут принимать произвольные значения)

m базисных переменных (выражаются через сво-

бодные переменные)

Задача ЛП, записанная в канонической форме, допускает геометрическое изображение (и решение) на плоскости, если число переменных

n m 2

В этом случае надо выразить все переменные через две из них, тогда задача описывается в виде

xi 0, i 1,2,...,n

Прямые

xk 0, k 1,2,...,n

(две из них будут осями координат), определяют на плоскости x1Ox2 границы выпуклого многоугольника, а

совместный учет допустимых полуплоскостей

xi 0

определяет допустимую область решений

(такой области не существует, если условия неотрицательности переменных противоречат друг другу)

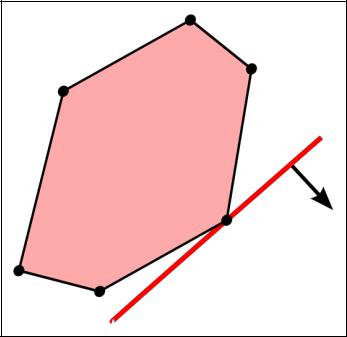
Коэффициенты ЦФ определяют семейство параллельных прямых на плоскости и направление, в котором увеличивается значение ЦФ.

В задаче минимизации прямую надо перемещать параллельно самой себе в сторону

уменьшения значений ЦФ до тех пор, пока она еще будет содержать точки многогранника допустимой области решений.

СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛП

Решение – любой набор переменных x1, x2 ,..., xn , удовлетворяющий уравнениям (5).

Допустимое решение – решение с неотрицательными переменными.

Базис – набор переменных, для которых матрица из коэффициентов этих переменных в уравнениях, будет невырожденной, т.е. ее определитель отличен от нуля.

Базисное решение – решение, которое получится, если положить все небазисные (свободные) переменные равными нулю и решить уравнения относительно базисных переменных.

Принцип нахождения оптимального решения

1)Записать задачу ЛП в канонической форме.

2)Определить допустимое базисное решение и проверить его оптимальность.

3)Если решение не оптимально, то из базиса вычеркнуть определенную переменную и вместо нее ввести другую. В результате многократного повторения описанного процесса будет:

a.получено оптимальное решение

b.выявлена противоречивость ограничений

c.станет видно, что при допустимых базисных решениях ЦФ неограничена

Замена базиса

Выведем в системе уравнений (7) yk из числа свобод-

ных и введем на ее место переменную xr и решим r-е уравнение системы (7) относительно yk :