Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

С. В. Галкин Кратные интегралы, ряды, поле

.pdf

Скачиваний:

191

Добавлен:

10.02.2015

Размер:

714.54 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Здесь 2

- оператор Лапласа (скаляр – оператор).

divgrad div

2 .

(divgrad)a 2Pi

2Qj 2Rk - произведение скаляр-оператора Лапласа на вектор a.

Гармоническое поле.

Скалярное поле x, y,z называется гармоническим, если

- уравнение Лапласа.

Векторное поле называется гармоническим, если оно потенциальное (a grad ), а

потенциал - гармоническое скалярное поле, т.е. 2

Теорема. Для того, чтобы векторное поле a(M)

было гармоническим, необходимо и

достаточно чтобы оно было соленоидальным и потенциальным.

Необходимость.

Если векторное поле a(M) - гармоническое,

то оно потенциальное,

т.е. a grad , тогда оно соленоидально, так как diva divgrad 2 0.

Достаточность. Если векторное поле a(M)

потенциальное, то a grad . Так как оно

еще и соленоидально, то 0 = diva divgrad 2 . Следовательно, поле потенциально и его потенциал удовлетворяет уравнению Лапласа, поэтому векторное поле – гармоническое.

Так как гармоническое поле потенциально и соленоидально, то его свойства – свойства соленоидального поля и свойства потенциального поля.

Часть 2. Числовые и функциональные ряды

Лекция 10. Числовые ряды и их свойства.


Числовой		ряд			an – это сумма					бесконечного количества чисел,					выбранных по
					n 1
определенному алгоритму. Обычно задают формулу общего члена ряда an .
Примеры
1. 1+	1	1		1		1	...	1	...-		бесконечно	убывающая			геометрическая
1. 1+		4					...	2n 1	...-		бесконечно	убывающая			геометрическая
2		4	8		16			2n 1		1			1
прогрессия со знаменателем q										1	. Ее сумма равна		1	2,
прогрессия со знаменателем q										2	. Ее сумма равна	1		2,
										2		1
												1
												1
												2

2.1+1+1+…..Сумма этого ряда бесконечна.

3.1-1+1-1… Сумма этого ряда не существует (ни конечная, ни бесконечная).

При изучении рядов возникает основной вопрос: «Сходится ли ряд». Отвечая на этот

вопрос для геометрической прогрессии, мы вычисляем последовательно S2 1+ 1 3, 2 2

S		=1+	1	1		7	,	S	4	1+		1		1		1	15	, - суммы n членов ряда – частичные суммы ряда
S	3	=1+		4			,	S		1+							8	, - суммы n членов ряда – частичные суммы ряда
	3	2		4	4						2		4		8		8
Sn .

		Ряд		an					называется						сходящимся, если				существует конечный	предел
					n 1
последовательности											частичных						сумм ряда –		он называется суммой	ряда

limn Sn S .

Ряд называется расходящимся, если предел частичных сумм ряда бесконечен или вообще не существует.

Необходимый признак сходимости ряда. Если ряд сходится, то limn an					0.
Доказательство.	an Sn Sn 1 .	Пусть	ряд	сходится,	тогда

limn an limn Sn limn Sn 1 S S 0.

Необходимый признак позволяет отсеивать часть расходящихся рядов.

Достаточный признак расходимости. Если limn an 0, то ряд расходится.

Доказательство (от противного). Пусть ряд сходится. Тогда	по необходимому
признаку сходимости ряда limn an 0 Противоречие с limn an 0 .

	3n 2					3
Пример. Ряд	3n 2			расходится, так как limn an		3	0
Пример. Ряд	2n 1			расходится, так как limn an			0
n 1	2n 1				2
	1		n
Пример Ряд 1				расходится, так как an e 0.
Пример Ряд 1				расходится, так как an e 0.
n 1		n

Критерий Коши сходимости ряда.

(Это – критерий Коши для последовательности частичных сумм ряда). Для того чтобы ряд сходился (последовательность частичных сумм

предел), необходимо и достаточно, чтобы 0 N, n N, p 0

Sn p

имела конечный

Sn .

Критерий Коши расходимости ряда. (отрицание критерия Коши)

Для того чтобы ряд расходился необходимо и достаточно, чтобы

0 N, n N, p 0									Sn p Sn		.
	Пример. Рассмотрим гармонический ряд												1

													n 1 n
													n 1 n
							1 1			1	1		1			1 1				1	1	1
	\| Sn p			Sn
					\|				...			...			1				...			...
					\|	1			...			...	n p	...	1				...			...
							2 3			n n 1			n p			2 3				n	n 1		n p
	1	...		1		p		1	, если выбрать p n . Удалось для								1	,	N,n выбрать			p n ,
	1			1		p		1									1
	n p		n p
	n p		n p			n p 2										2

чтобы Sn p Sn . Следовательно, гармонический ряд расходится.

Свойства сходящихся рядов.

1.Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.

Доказательство.	Для	второго	ряда	частичная	сумма	будет	равна
S2 n ka1 ... kan	k a1	... an kS1n . По		теореме о	предельном переходе в

равенстве S2 kS1 .

2.Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.

Сгруппируем члены ряда, например, так

b1 a1 .. ak , b2

ak 1 ...

al ,...bn

as ...

ap.... Видно, что частичные суммы

группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу.

3. В сходящемся	ряде	можно отбросить конечное	число первых членов
a1...ak (a1 ... ak	B).	Полученный ряд будет сходиться,	а его сумма будет меньше
суммы исходного ряда на B.

Запишем частичные суммы второго ряда

S21 ak 1 S1k 1 B,...S2 n ak 1 ... ak n S1k n B . По теореме о предельном переходе в равенстве S2 S1 B.

Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов,

называется остатком ряда и обозначается Rk an

n k 1

4.Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3).

Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».

5.Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.


Рассмотрим два сходящихся ряда an	и bn	. Рассмотрим ряд cn , где
n 1	n 1	n 1

cn an bn . Sc n Sa n Sb n . Переходя к пределу в равенстве, получим Sc Sa Sb .

Примеры.

1.Ряд –5+7-8+100+1+0,5+0,25+0,125+… сходится. В самом деле, отбросив первые четыре члена ряда (свойства 3,4), получим сходящуюся бесконечно убывающую геометрическую прогрессию

2.Ряд 1 1 1 1 1 1 1 1 ...расходится. Он представляет собой сумму двух

2 2 4 3 8 4

рядов: сходящейся геометрической прогрессии (нечетные члены) и гармонического ряда (четные члены). Если бы этот ряд сходился, то, вычитая из него почленно

сходящийся ряд 1 0 1 0 1 ..., мы должны были бы по свойству 5 получить

2 4

сходящийся ряд. А получаем расходящийся гармонический ряд. Следовательно, исходный ряд расходится.

3.	Ряд			1			1		...			1			...сходится. Рассмотрим сходящийся ряд
							2 3
			1 2								n(n 1)
			1			1				1		1					1 1
	1												...					... 1. Группируем его члены

		2				2			3			3					n n
	1				1	1						1		1
1									...							..., получаем исходный ряд. Следовательно, он
														2 3
		2			2			3			1 2

сходится (свойство 2), и его сумма равна 1.

Лекция 11 Знакоположительные ряды.

Числовой ряд называется знакоположительным, если все его члены – положительные (неотрицательные) числа.


an	an 0
n 1

Основная и довольно приятная особенность знакоположительных рядов в том, что частичные суммы ряда представляют собой неубывающую последовательность.

Sn Sn 1 an Sn 1, т.к. an 0.

Поэтому достаточно проверить, что последовательность частичных сумм ограничена сверху, чтобы по теореме Вейерштрасса утверждать, что последовательность частичных сумм имеет конечный предел, т.е. ряд сходится.

На этом основаны, практически, все признаки сходимости рядов.

Ряд может сравниваться с несобственным интегралом (интегральный признак Коши), с другими рядами (признаки сравнения рядов), в частности, со сходящейся геометрической прогрессией (признак Даламбера, радикальный признак Коши).

Каждый признак можно сравнить с увеличительным стеклом. У каждого признака есть своя область применения, более широкая или более узкая (как поле зрения линзы) и своя сила. Одни признаки сильнее, позволяют различать слабо сходящиеся или слабо расходящиеся ряды, но имеют узкую область применения (например, интегральный признак Коши). Другие, наоборот, имеют широкую область применения, но довольно слабы, ряды, близкие к границе сходимости, с их помощью не различишь (например, признаки Даламбера и Коши (радикальный)).

Пока в библиотеке рядов, которые мы можем использовать для сравнения, всего два ряда: сходящийся ряд - бесконечно убывающая геометрическая прогрессия, известная еще из школы, и гармонический ряд, расходящийся по критерию Коши.

Заметим, что критерий Коши (как критерий сходимости), вообще, самый сильный инструмент при исследовании сходимости ряда, но его область применимости узка.

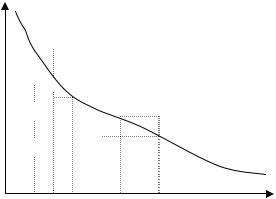
Интегральный признак Коши, основанный на сравнении с несобственным интегралом – очень сильный признак. В самом деле, если аппроксимировать непрерывную подинтегральную функцию кусочно-постоянной, то площадь под графиком функции (интеграл) и площадь под графиком кусочно-постоянной функции будут различаться на конечное число.

f(x), an

a1 a2

an-1

1 2

n-1

Доказательство.

Интегральный признак Коши.
Пусть при		x 1 определена непрерывная, не
возрастающая функция				f(x), такая, что
f (n) an ,		limx f (x) 0.

Тогда	ряд	an	сходится	тогда и только
		n 1
тогда,	когда		сходится	несобственный

интеграл f (x)dx .

f (x)dx - это площадь под графиком функции f (x) при 1 x n.

Так как a2 a3 ... an Sn a1 (сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а a1 a2 ... an 1 Sn an ограничивает ее сверху,

то Sn a1 f (x)dx Sn an .

									46
								n
Достаточность.		Если интеграл			сходится,		то	Sn a1 f (x)dx a1 f (x)dx,
поэтому последовательность Sn								1	1
поэтому последовательность Sn			ограничена сверху. Так					как эта последовательность не

убывает, то по теореме Вейерштрасса limn Sn						S . Поэтому ряд an сходится.
								n 1

Необходимость. Если ряд			an сходится,			то	limn Sn S ,		а по необходимому
			n 1
признаку	сходимости	ряда	an	0	при	n .		Поэтому	последовательность
n
f (x)dx (неубывающая, так как				f (x) 0) ограничена сверху. Следовательно, по теореме
1
		n
Вейерштрасса limn f (x)dx f (x)dx, т.е. несобственный интеграл сходится.
		1	1

Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного.

Поэтому говорят, что несобственный интеграл и ряд сходятся или расходятся «одновременно», т.е. если один из них сходится, то и другой сходится, если один расходится, то и другой расходится. Это понятие часто употребляют при сравнении рядов.

Пример. Применим интегральный признак к гармоническому ряду.

			b	1
1	1	dx limb 1			dx limb lnb ln1	-	интеграл	расходится,	поэтому	и
	x			x
гармонический ряд расходится.						1

Пример.			Рассмотрим «ряды Дирихле»				. Название	взято в	кавычки,	так
						p
					т 1 n

неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы.

1 xp limb b1 p 1 p 1 . Ясно, что интеграл сходится при p>1 и расходится при

p<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод

		1	сходится при p 1
						.
		p
	т 1 n		расходится при p 1
					1
	Интересно, что			ряд			сходится при q 1и расходится при q 1, интегралы
					q
				n 1	nln	n
	1		1
		,		расходятся (проверьте по интегральному признаку).
			nlnnlnlnn
n 2	nlnn n 3

Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.

		47
Признаки сравнения рядов.
Первый признак сравнения рядов.

Пусть выполнено неравенство an bn	n. Тогда из сходимости ряда	bn следует
		n 1

сходимость ряда an , а из расходимости ряда an следует расходимость ряда bn .

n 1

Замечание. В силу свойства сходящихся рядов, отбюрасывание конечного числа членов ряда не влияет на сходимость и неравенство an bn можно проверять «начиная с

некоторого n». Поэтому эту фразу часто можно встретить в теоремах о рядах. Иногда ее просто опускают, но ее всегда надо иметь в виду.


Доказательство. 1) Пусть ряд bn сходится. Тогда		выполнено неравенство
	n 1	Sa n ограничена сверху
Sa n Sb n Sb	n. Поэтому последовательность частичных сумм	Sa n ограничена сверху

числом Sb . Но эта последовательность не убывает. Следовательно, по теореме Вейерштрасса

limn Sa n

Sa Sb .

Последнее неравенство справедливо в силу теоремы о предельном

переходе в неравенстве.

2) Пусть ряд an расходится. Если

ряд bn сходится, то по п.1 доказательства и ряд

n 1

an сходится. Противоречие. Следовательно,

ряд bn расходится.

n 1

Пример. Ряд

расходится,

так

как

, а

ряд

(гармонический)

расходится.

n 2

lnn

ln n n

n 2

Второй признак сравнения.

Пусть

limn

C 0. Тогда

ряды

сходятся

или расходятся

n 1

«одновременно», т.е. если один из них сходится, то и другой сходится, если один расходится, то и другой расходится.

Доказательство. Раскроем определение предела. 0 N , n N						an	C	.
Доказательство. Раскроем определение предела. 0 N , n N						bn	C	.
						bn
С	an	C ,	b (C ) a	n	b (C ).
С		C ,	b (C ) a		b (C ).
	bn		n		n
	bn

Если ряд an сходится, то по				1	признаку сравнения ряд bn (C ) сходится
		n 1			n 1

(C 0, так как мало) , ряд bn сходится (свойство сходящихся рядов).

n 1

Если ряд bn сходится, то ряд bn (C ) сходится (свойство сходящихся рядов),

n 1

тогда по 1 признаку сравнения ряд an сходится.

		n 1

Пусть	ряд	an расходится.	Если	ряд	bn сходится,	то	по	предыдущему	ряд
		n 1			n 1

an сходится (противоречие).
n 1

Пусть	ряд	bn расходится.	Если	ряд	an сходится,	то	по	предыдущему	ряд
		n 1			n 1

bn сходится (противоречие).

n 1

Пример.

4n 2

Ряд с

расходится

по второму признаку

сравнения

(ряд

n 5

сравнения – гармонический ряд).

sin

n 1

n , arctgn -

Ряд

сходится. sin

ограничена.

Ряд

narctgn

n 2

сравнения

- сходящийся ряд Дирихле.

n 2

Признак Даламбера.

Конечная форма признака Даламбера.

an 1

Пусть n N

q 1,

тогда ряд an сходится.

n 1

an 1

Пусть n N

q 1,

тогда ряд an расходится.

n 1

Доказательство. Пусть n N

an 1

q 1.

Тогда a

n 1

q3a

n 2

... qna .

a a

... a

a q ... a qn 1

a (1 q q2

... qn 1)

ряд

1 q

an сходится.

Можно

было, не оценивая

частичную сумму ряда, заключить,

что

ряд

n 1

сходится по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.

Пусть n N

an 1

q 1, Тогда a

a , a

q2a

a ...a

qn 1a

a .

Поэтому an не стремится к нулю при n , необходимый признак сходимости ряда не

выполнен, ряд an расходится.

n 1

Предельная форма признака Даламбера.

an 1

Пусть limn

q 1,

тогда ряд an сходится. Пусть limn

q 1, тогда ряд

n 1

an 1

an расходится.

Если

limn

q 1, то признак не позволяет

сделать вывод о

n 1

сходимости или расходимости ряда.

an 1

Доказательство. Пусть lim

q 1. Тогда 0 N ,что n N

При малом

0 q

an 1

q 1. По конечной форме признака Даламбера ряд

an сходится.

n 1

an 1

Пусть lim

q 1. Тогда

0 N ,что n N

. При

малом

1 q

an 1

то есть n N

an 1

an . Поэтому an не стремится к нулю при

n ,

необходимый признак сходимости ряда не выполнен, ряд an расходится.

n 1

Замечание. Признак Даламбера удобно применять, когда общий член ряда содержит произведение некоторых чисел или факториал.

Правда, если общий член ряда содержит факториал, то его можно заменить по формуле

n n

Стирлинга n!~ 2 n при n и применять второй признак сравнения.

Пример. n 1 nn .

n 1

(n 1)!nn

1. Ряд сходится по

lim

n an

n (n 1)n

(n 1)n 1 n!

признаку Даламбера.

enn!

Пример. n 1 nn

. Рассмотрим	a	n 1	en 1 n 1!nn		e n 1 nn

	an		(n 1)n 1		n 1 n 1 n
				enn!

			50
	e		1, так
	1	n	1, так
	1	n
1
1

	1 n
как последовательность 1		, монотонно возрастая, стремится к e	при n , то

n N	an 1	1	. Следовательно, n N					an 1 an . Поэтому an не стремится к нулю
n N		1	. Следовательно, n N					an 1 an . Поэтому an не стремится к нулю
	an

при n , необходимый признак сходимости ряда не выполнен, ряд an расходится.
									n 1
Заметим, что			lim	n	an 1	e			1. Поэтому признак Даламбера в
Заметим, что			lim				1 n		1. Поэтому признак Даламбера в
					an		1 n
						limn 1
						limn 1
							n

предельной форме не дает ответ о сходимости или расходимости ряда, хотя признак в конечной форме позволяет установить расходимость ряда.

Радикальный признак Коши.

Конечная форма радикального признака Коши.

Пусть n N

q 1, тогда ряд an сходится.

n 1

Пусть n N

q 1, тогда ряд an расходится.

n 1

Доказательство.

Пусть n N n

q 1. Тогда

qn , q 1,

ряд an

сходится

n 1

по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.

Пусть n N

q 1.

Тогда

an qn 1,

ряд

an расходится,

так как

необходимый признак сходимости ряда не выполнен.

n 1

Предельная форма радикального признака Коши.

Пусть limn

q 1,

тогда ряд an сходится.

n 1

Пусть limn

q 1,

тогда ряд an расходится.

n 1

Доказательство. Пусть limn

q 1, тогда 0

N, n N

q 1

при малом

Ряд an сходится по конечной форме радикального

n 1

признака Коши.

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.201868.1 Кб2Рынки (Обществознание) 9 октября 2011.doc
#
09.12.2018849.92 Кб36РЯДЫ.doc
#
09.02.2015942.08 Кб86с 1 по 20.doc
#
09.02.20152.79 Mб22с 21 по 32.doc
#
09.02.20153 Mб12с 33 до конца.doc
#
10.02.2015714.54 Кб191С. В. Галкин Кратные интегралы, ряды, поле.pdf
#
16.11.201951.65 Кб11с.р.1.docx
#
10.02.2015124.38 Кб30С2. МОИ. Задачи.pdf
#
10.02.2015203.57 Кб44С2.МОИ.План занятий (с теорией и задачами).pdf
#
09.02.2015417.15 Кб7сады и парки.docx
#
01.11.20185.69 Mб78Саймон Кэнн - Как создать звук (How To Make A N....docx