Министерство образования и науки Российской Федерации Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана» (КФ МГТУ им. Н.Э. Баумана)

ФАКУЛЬТЕТ	"Электроники, информатики и управления"
КАФЕДРА	"Конструирование и производство электронной аппаратуры"

О Т Ч Е Т

Домашнее задание №1

ДИСЦИПЛИНА:	"Функциональная логика и теория алгоритмов "
ТЕМА:	"Основные алгоритмы теории графов"

Выполнил: студент гр. РПВ.Б-31	Тер-Погосян Р.Э.
Проверил:	Соловьёв И.В.

Дата сдачи (защиты ) домашней работы:
Результаты сдачи (защиты): Количество рейтинговых баллов
Оценка	зачтено

Калуга, 2014г.

Cрок выполнения: 17 неделя.

Содержание отчёта:

- краткие теоретические сведения;

- листинги программ расчёта минимальных расстояний в графе;

- скриншоты окна консоли;

- выводы.

Теоретические сведения.

Алгоритм Дэйкстры.

Алгоритм создан голландским учёным Э. Дэйкстрой в 1959 году для нахождения минимального расстояния и кратчайшего пути из одной вершины до всех остальных, в графе, не имеющим отрицательных рёбер.

Выбирается начальная вершина. Каждой из вершин в соответствие ставится метка - число, равное наименьшему известному расстоянию от данной вершины до начальной вершины. На каждом шаге алгоритм посещает одну из вершин и пытается уменьшить метки. Работа алгоритма завершается, когда все вершины посещены.

При инициализации начальной вершине присваивается нулевая метка, всем остальным вершинам присваиваются метки равные бесконечности, это отражает неизвестность длины пути.

В некоторых случаях вместо бесконечности присваивают числа, большие максимально возможной длине пути в графе. Все вершины отмечаются как непосещенные.

В основном цикле из непосещенных вершин выбирается v1 - вершина с минимальной меткой M. Рассматривается каждая непосещенная соседняя вершина v. Пусть такой вершиной будет v2. Расстояние от v1 до v2 равно D, метка вершины равна N. Рассматривается новая длина пути, равная сумме метки вершины v1 и длины ребра от v1 до v2: D+M. Далее эта сумма сравнивается с текущей меткой вершины v2 – N. Если N > D+M, то метка вершины v2 заменяется на D+M, если N < D+M, то метка вершины v2 остаётся той же N. После того, как все соседние v1 вершины проверены, v1 отмечается как посещённая. Цикл повторяется до тех пор, пока все вершины не будут посещены.

Наименьшие длины пути до каждой из вершин из начальной вершины будут храниться в метках этих вершин по завершении работы алгоритма.

Пример работы алгоритма.

Пусть задан граф (рис. 1), синим цветом обозначены веса рёбер графа. Найти наименьшую длину пути из вершины 0 во все остальные, используя алгоритм Дэйкстры.

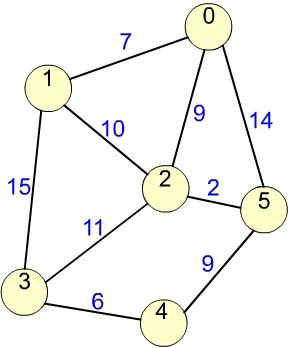
Рис. 1

Произведём инициализацию. Начальной вершине 0 присвоим метку равную нулю, всем остальным вершинам присвоим метки равные бесконечности, так как минимальное расстояние до них неизвестно (рис 2).

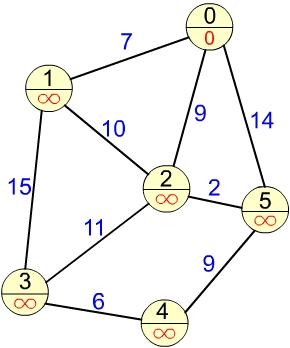
Рис. 2

Выбираем вершину с минимальной меткой из непосещенных. Такой вершиной будет 0. Соседями данной вершины являются вершины 1, 2 и 5 с расстояниями до них 7, 9 и 14 соответственно. Сначала рассмотрим вершину 1, так как расстояние до неё меньше. Длина пути в вершину 1 через 0 равна сумме кратчайшего расстояния до 0 (значению её метки) и длины ребра 0-1: 0 + 7 = 7. Данная сумма меньше чем текущая метка вершины 1 равная бесконечности, поэтому заменяем метку на 7. Далее рассмотрим вершину 2. Сумма метки исходной вершины и длины пути 0-2 равна: 0 + 9 = 9. Это меньше текущей метки вершины 2 равной бесконечности, поэтому заменяем её на 9. Аналогично для вершины 5. Сумма метки исходной вершины и длины пути 0-5 равна: 0 + 14 = 14. Это меньше текущей метки вершины 5 равной бесконечности, поэтому заменяем её на 14 (рис. 3).

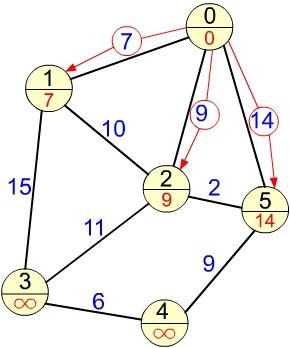
Рис. 3.

Все соседние вершины рассмотрены, отмечаем вершину 0 как посещённую. На следующем шаге снова выбирается вершина с минимальной меткой из непосещённых. В нашем случае это вершина 1 с меткой 7. Соседями данной вершины являются 3 и 2. Вершина 0 не рассматривается, так как она уже посещена. Рассматриваем длину пути в вершину 2 из 1, равную кратчайшему расстоянию до 1 (значению её метки) и длины ребра 1-2: 7 + 10 = 17. Так как 17 больше текущей метки вершины 2, оставляем метеку неизменной и равной 9. Для вершины 3: 7 + 15 = 22. Заменяем текущую метку вершины 3 на 22 (рис. 4). Все соседние вершины 1 рассмотрены, отмечаем её как посещённую.

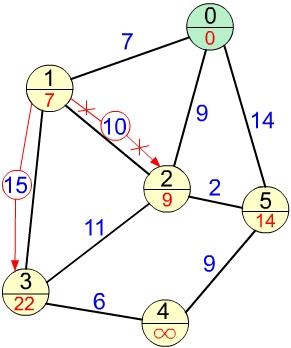
Рис. 4

Дальнейшие шаги алгоритма производятся аналогично, они показаны на рисунке 5.

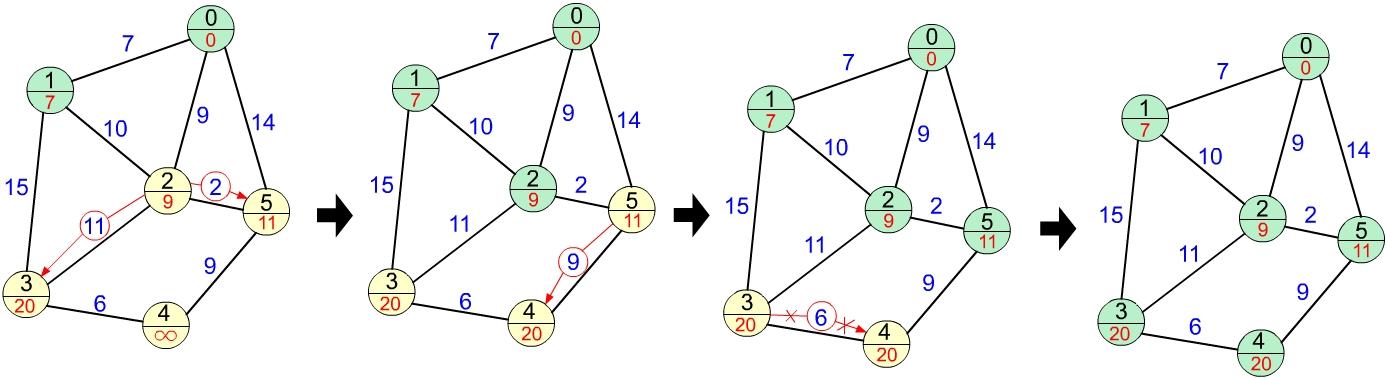
Рис. 5

Алгоритм завершает свою работу, когда все вершины будут посещены. Метки каждой вершины будут соответствовать минимальному кратчайшему расстоянию от этой вершины до 0 вершины, например, минимальное расстояние от вершины 0 до вершины 4 будет равно 20 (9+2+9).