Лекция 3

Лекция 3.

Объект проектирования и его математическая модель.

Математическая модель – это совокупность математических объектов (чисел, переменных, векторов, множеств и т.д.) и отношений между ними, которая адекватно отображает некоторые свойства проектируемого объекта. Например, большой и важный класс математических моделей составляет система уравнений. В общем случае уравнения математической модели связывают физические величины, которые характеризуют состояние объекта и не относятся к выходным, внутренним или внешним параметрам (например, скорости и силы в механических системах; давления и расходы в гидравлических системах; электрические напряжения, токи и заряды в электрических системах и т.д.). Эти величины называют фазовыми переменными. Вектор фазовых переменных задает точку в пространстве, называемом фазовым пространством. Внутренние параметры – это параметры элементов. Внешние параметры – это параметры внешней по отношению к объекту среды, оказывающие влияние на его функционирование. Выходные параметры – показатели качества, по которым можно судить о правильности функционирования системы (объекта).

Обычно при составлении математических моделей в получающихся уравнениях фигурируют не все фазовые переменные физической системы, а только часть из них, достаточная для однозначной идентификации состояния объекта. Назовем такие фазовые переменные базисными координатами (обозначим их вектором V). Через базисные координаты могут быть вычислены и все остальные фазовые переменные. Тогда в общем случае объекта с сосредоточенными параметрами его математическую модель можно представить в виде: .

В модель входят также коэффициенты при фазовых переменных. Например, для электрической схемы фазовыми переменными будут напряжение и токи, а коэффициенты при них определяются через внутренние параметры (сопротивления, емкости, индуктивности. Пример: ;

Е, i – фазовые переменные;

L, R – внутренние параметры.

Математические модели на различных блочно-иерархических

уровнях проектирования.

При проектировании выделяют три уровня иерархического деления проектируемого объекта: нижний (В), средний (Б) и высший (А).

Низший уровень (В) – его называют уровнем проектирования базовых элементов или микроуровнем. На этом уровне при моделировании фазовые переменные фигурируют как функции нескольких независимых переменных, к которым относятся пространственные координаты и время, изменяющиеся непрерывно. Элементами этого уровня являются участки объемной структуры. Типичными фазовыми переменными уровня В будут плотности потоков, напряженности полей, концентрации частиц, поле температур. Внутренними параметрами могут быть, например, такие величины, как коэффициенты теплопроводности, концентрации примесей, геометрические размеры элементарных участков, а выходными параметрами – электрическое сопротивление резистора, фокусное расстояние линзы, жесткость пружины. Математические модели данного уровня представляют собой дифференциальные уравнения в частных производных. Такие модели часто называют распределенными моделями. Решение дифференциальных уравнений в частных производных представляет значительные вычислительные трудности. Рост сложности уравнений приводит к необходимости перехода на следующий более высокий уровень проектирования (уровень Б).

Средний уровень (Б) – здесь используют представление о средах как о дискретном пространстве. Эта дискретизация означает переход от распределенных к сосредоточенным моделям. Уровень Б называют также макроуровнем. Элементами этого уровня являются объекты, которые на микроуровне рассматривались как системы (например, резисторы, транзисторы в радиоэлектронных схемах). Параметры этих элементов будут на микроуровне выходными, здесь же они становятся внутренними. Примерами выходных параметров уровня Б являются коэффициент усиления усилителя, сила тяги двигателя и т.д. Типичными фазовыми переменными являются токи и напряжения в электрических системах, скорости и силы в механических системах, потоки и давления в гидравлических и пневматических системах. Математические модели уровня Б – это обыкновенные дифференциальные уравнения, в частных случаях статистических задач, переходящие в алгебраические и трансцендентные уравнения. С ростом числа элементов и соответственно порядков систем уравнений возможности решения задач на основе математических моделей уровням Б резко снижаются, становится необходимым переход к представлениям следующего, еще более высокого, уровня А.

Высший уровень (А) – его называют информационным. Системы этого уровня – сложные устройства и комплексы типа вычислительных машин и др. функционирование систем рассматривается в дискретные моменты времени. Дискретность представления пространства и времени обуславливает дискретность фазовых переменных, которыми являются величины, характеризующие состояние элементов. Роль элементов и внутренних параметров выполняют системы и выходные параметры уровня Б. так, элементами ЭВМ на уровне А можно считать арифметическое устройство, оперативную память и т.д. (в сварочном автомате: привод перемещения сварочной горелки, привод перемещения электродной проволоки, источник питания и др.). Выходными параметрами на уровне А являются: производительность автомата, его стоимость, масса и т.д.

В принципе в каждом рассматриваемом уровне могут быть подуровни более детального деления систем.

Макромодели. На каждом уровне (В, Б, А) следует различать математические модели элементов ……………….……. математические модели системы, получаемые непосредственным объединением математических моделей элементов в общую систему уравнений, называют полными математическими моделями. Математические модели более простые относительно полных (с точки зрения затрат машинного времени или памяти при их использовании) называют макромоделями (макромодель – это аппроксимация полной модели).

Требования к математическим моделям (прежде всего это требования точности, экономичности, универсальности).

Точность математической модели – ее свойство, отражающее степень совпадения предсказанных с помощью нее значений параметров объекта с истинными значениями этих параметров. Обычно в качестве оценки точности математической модели используют векторную оценку, которую сводят к скалярной используя понятие нормы вектора. Так, например, если объект характеризуется выходными параметрами Y_j , где j = 1,2, ... ,m, а значения тех же параметров, полученных при использовании математической модели – Y_Mj , то вектор относительной погрешности ε = (ε₁, ε₂, … , ε_j, … , ε_m), где

ε_j = (Y_j – Y_Mj) / Y_j.

Здесь в качестве оценки точности можно использовать максимальный компонент вектора погрешности, т.е. ε_max = max | ε_j |, j Є [1:m] , либо среднеквадратическое значение вектора .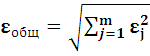

Экономичность математической модели – определяется затратами машинного времени Т_М. Это время счета по этим моделям, его можно оценить количеством арифметических операций, выполняемых при однократной реализации уравнений модели.

Степень универсальности математической модели – определяется применимостью математической модели к группе однотипных объектов, к их анализу в одном или многих режимах функционирования.

Все три приведенных выше требования друг относительно друга противоречивы. Чем детальнее в модели отражаются различные закономерности процессов, тем точнее и универсальнее модель, но тем больше требуемый объем вычислений по математическим моделям. Поэтому часто трудно найти компромисс по всем показателям и проектировщик идет на вариант использования нескольких моделей одного элемента, обладающих лучшими показателями по каждому критерию.

Классификация математических моделей.

В зависимости от характера отображаемых свойств проектируемого объекта математические модели делятся на функциональные и структурные.

Функциональные математические модели – отражают процессы функционирования объекта. Они чаще всего имеют форму систем уравнений.

Структурные математические модели – обычно задаются в форме матриц, графов, списков векторов. Они выражают взаимное расположение элементов в пространстве, наличие непосредственных связей между элементами (узлы, проводники). При их описании обычно абстрагируются от физической сущности процессов в объекте.

По способу получения функциональные математические модели делятся на теоретические и формальные.

Теоретические математические модели получают на основе изучения физических закономерностей, структура уравнений и параметры математической модели имеют определенное физическое толкование.

Формальные математические модели – получают путем обследования связей входных и выходных параметров объекта, считая его как «черный ящик».

Теоретический подход в большинстве случаев позволяет получать математические модели более универсальные, справедливые для широкого диапазона изменения внешних параметров. Формальные математические модели по сравнению с теоретическим обычно более точны в окрестностях той точки пространства параметров, в которой производились измерения, но менее точны в дали от этой точки.

Ряд признаков классификации математических моделей связан с особенностями уравнений. В зависимости от линейности или нелинейности уравнений математические модели делятся на линейные и нелинейные.

В зависимости от мощности множества значений переменных математические модели делятся на непрерывные и дискретные.

В непрерывных математических моделях все входящие в них переменные непрерывны, получаемые варианты решений по ним имеют мощность континимума.

Переменные дискретных математических моделей – дискретные величины, множество решений ………………

По форме связей между выходными, внутренними и внешними параметрами различают модели в виде систем управлений и системы в виде явных зависимостей выходных параметров от внутренних и внешних. Первые из них называют алгоритмическими, вторые – аналитическими. В зависимости от того учитывают уравнения математических моделей инерционность в объекте или не учитывают, различают математические модели динамические и статические.

Математические модели на иерархическом уровне В

(теоретические математические модели элементов объекта).

При создании теоретических математических моделей целесообразно исходить из основных физических законов в их наиболее «чистом», фундаментальном виде. К наиболее общим фундаментальным законам в первую очередь относятся законы сохранения массы, количества движения, энергии. Общая формулировка этих законов, помогающая перейти к математическим уравнениям, может быть ………. следующим образом: изменение ……….. этой субстанции через поверхность элементарного объема. В качестве субстанции может выступать масса, количество движения, энергия.

Общий вид уравнения теоретической модели, согласно определению, можно дать в форме:

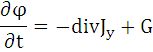
где 𝝋 – некоторая фазовая переменная, выражающая субстанцию (плотность, энергию, импульс);

– поток фазовой переменной;

G – скорость генерации субстанции;

t – время.

Поток фазовой переменной есть вектор , дивергенция этого вектора, как и любого другого, определяется формулой:

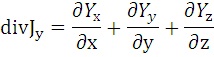
и характеризует сумму притока – стока субстанции через поверхность элементарного объема.

1. Уравнение закона сохранения массы имеет вид:

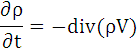
ρ – плотность массы; V – скорость.

При одномерной задаче (в направлении оси Х) это уравнение преобразуется в вид:

2. Уравнение закона сохранения энергии:

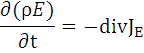
где E = e + V²/2 – полная энергия массы;

J_E – поток энергии;

е – внутренняя энергия единицы массы.

В одномерном случае:

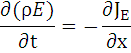
3. Уравнение закона сохранения количества движения (импульса) без учета внешних сил в одномерном приближении записывается:

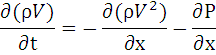
P – давление.

Все эти уравнения (уравнения законов сохранения) лежат в основе математических моделей многих механических, тепловых, гидроаэродинамических устройств при их проектировании на иерархическом уровне В.

На основе уравнения закона сохранения массы рассмотрим более подробно уравнение теплопроводности, которое широко используется при описании тепловых сварочных процессов. Это уравнение связывает изменение температуры во времени и пространстве со свойствами свариваемого материала. Общий вид уравнения теплопроводности можно получить из уравнения сохранения энергии:

Q – количество теплоты; J_Q – вектор плотности теплового потока; G_Q – количество теплоты, выделяемой в единицу времени в рассматриваемом элементарном объеме.

Обозначив через С удельную теплоемкость системы, можно связать изменение количества теплоты dQ с изменением температуры dT:

Плотность теплового потока J_Q выражается через градиент температуры в соответствии с законом Фурье:

λ – коэффициент теплопроводности.

Получим уравнение теплопроводности:

Для однородного изотропного тела λ = const. Тогда

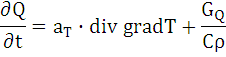
а_Т = λ / Сρ – коэффициент температуропроводности.

В одномерном приближении:

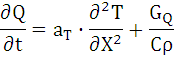
Математическая модель компонента тепловой системы получается, если к уравнению теплопроводности добавить зависимость G_Q от пространственных координат и времени, а также сформулировать краевые условия. Начальные условия должны иметь вид Ф(x,y,z,T) = 0 для t = 0. Граничные условия: для автономного элемента должна быть задана температура на его поверхности T_П или плотность теплового потока на поверхности J_QП.

Уравнение теплопроводности описывает процессы изменения температуры в телах за счет явления теплопроводности. Одним из видов теплопроводности может быть явление конвекции между жидким металлом и твердым телом (сварочная ванна и закристаллизовавшийся металл). При конвекции условия теплообмена подчиняются закону Ньютона:

J_Q = а_конв · (Т₂ – Т₁)

а_конв – коэффициент теплоотдачи через конвекцию; Т₁ – температура жидкости вдали от твердого тела; Т₂ – температура твердого тела без учета тепловой конвекции.

Основной результат решения уравнения теплопроводности – получение температурных полей в твердом теле и определение на основе их геометрических размеров зоны проплавления и возможных структурных изменений в шве.

Лекция.

Макромодели на основе метода теории размерностей.

При проведении активного эксперимента измерение ряда технологических параметров трудно реализуемо из-за отсутствия надежных датчиков. Поэтому для получения математических моделей сложных технологических объектов удобно использовать теорию подобия и размерностей.

Для правильного применения теории размерностей исследователь должен знать характер и число фундаментальных (основных) переменных, определяющих физические явления процесса. Фундаментальной (основной) переменной будем называть любую величину, оказывающую влияние на эксперимент и способную изменяться от других переменных (первичных), составляющих размерность основных переменных величин. Если основные переменные процесса известны, то их можно объединить в безразмерные комплексы. Количество получаемых безразмерных комплексов определяется π – теоремой Букенгема: число безразмерных комплексов равно числу всех физических разнородных величин, существенных для процесса, за вычетом числа первичных величин.

Следовательно, если физический процесс определяется числом m основных фундаментальных переменных и числом n первичных величин (m > n), то число получаемых безразмерных комплексов π: N = m – n.

Комплексы в этом случае находятся с помощью определительных уравнений, получаемых из физических формул подстановкой в них вместо физических переменных их выражений в символах размерностей.

Рассмотрим на конкретных примерах применение методов теории подобия и размерностей для получения аналитических выражений, по которым можно рассчитывать размеры шва при автоматической сварке в среде аргона и под флюсом.

Лекция.

Математические модели на основе теории

подобия и размерностей.

Для удовлетворения условия безразмерности необходима корректная запись уравнения (1), т.е. размерность У должна совпадать с комбинированной размерностью в знаменателе. Ясно, что никакого влияния на относительный оператор не может оказать масштаб измерения первичных величин. Укажем два метода получения безразмерных комплексов из определительных уравнений, в основе которых лежит π – теорема Букенгема. Любое определительное уравнение возможно записать в символах размерностей:

(2)

В этом уравнении обычно координируют символами размерности (длина – L, масса – М, время – Т, температура – Ө и т.д.). Комплекс π определяется отношением вторичной величины к первичным:

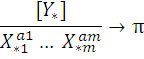
I метод – метод Рэлея.

Рассмотри пример. Пусть процесс определяется числом m вторичных величин, являющихся функцией 𝝋_К (где К = 1 … m) от первичных, количество которых n. Тогда можно записать систему определительных уравнений: 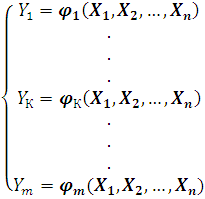(3)

Выберем из m вторичных величин одну искомую (пусть Y_К), тогда из системы (3) возможно в размерном виде написать связь:

m = 3, n = 2, тогда имеем

или

(4)

a₁ и а₂ – неизвестные.

Уравнение (4) должно быть однородным относительно размерности. Пусть:

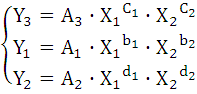
V = l · T^-1

Следовательно, с учетом (4) и в условиях однородной размерности можно составить два уравнения:

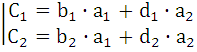(5)

с₁, с₂, b₁, b₂, d₁, d₂ – известны из условия задачи; а₁ и а₂ – неизвестные.

Из (5) определим а₁ и а₂.

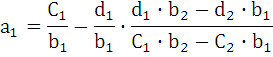
Следовательно, возможно однозначно записать безразмерный комплекс из переменных Х₁ и Х₂.

Пример.

Пусть необходимо найти закономерности движения несжимаемой жидкости (коэф. трения) в длинной цилиндрической трубе. Анализ явления вскрывает следующие фундаментальные переменные, сведенные в таблицу 1.

Метод Рэлея (составление определительных уравнений).

Таблица 1.

Наименование переменной	Обозначение	Форма размерности
Коэффициент трения (определяемая величина)	f, м	L	Первичные величины задачи L, М, Т
Диаметр трубы	d, м	L
Средняя скорость жидкости в трубе	V, м/с	L·T-1	Вторичные величины d, V, ρ, μ
Плотность жидкости	ρ, кг/м3	M·L-3
Динамическая вязкость	μ, кг/(м·с)	M·L-1·T-1

M – масса, Т – время, L – длина основные единицы.

Пусть все величины связаны соотношением:

или

т.е. в уравнении имеем четыре фундаментальных переменных.

Согласно π – теореме Букенгема, это функциональное соотношение (если оно однородно) можно выразить через безразмерные комбинации величин.

Подставим в уравнение вместо символов размерности из таблицы 1:

Чтобы уравнение было однородным относительно размерностей, должны выполняться следующие соотношения между показателями степени:

для М: 0 = с + d;

L: 1 = a + b – 3c – d;

T: 0 = – b – d.

Имеем три уравнения с четырьмя неизвестными. Упростим их исключив «с» и «d». с = – d; b = – d; a = 1 + b; с = b.

Подставляя эти соотношения для показателей степени получим:

Объединив члены с одинаковыми показателями степени, легко получить безразмерную комбинацию:

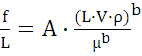(6)

Зная, что кинематическая вязкость υ = μ / ρ, из безразмерного комплекса получаем известный критерий Рейнольдса:

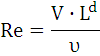
т.е. , lg f = lg n + lg Re.

Суть уравнения (6) состоит в том, что в нем мы имеем дело не с 4 переменными, а для определения f в качестве переменной рассматриваем безразмерный комплекс. Окончательный вид функции может быть найден экспериментальным путем.

Существенным здесь является и то, что можно говорить о подобных явлениях. Одинаковые значения критерия Рейнольдса (Re = idem) для каких-либо режимов течения жидкости означает подобие таких режимов. Поэтому, определив опытным путем, например, сопротивление трубы одного какого-либо сечения в зависимости от расхода воды, можно полученные результаты распространить на течение других жидкостей в трубах другого сечения, если только для них Re=idem.

Из теории подобия нельзя непосредственно определить вид функции зависимости для исследуемого процесса. Но построив с помощью теории подобия безразмерные комплексы, определяющие этот процесс, и найдя из ограниченного числа экспериментов для какого-либо частного случая зависимость между этими комплексами (критериями) в виде так называемых уравнений связи, можно распространить полученную зависимость на все подобные процессы: π₁ = π₂ и т.д.

Критерии подобия широко используют при решении различных задач, связанных с переносом теплоты и массы.

Второй метод построения комплексов рассмотрим на примере расчета величины проплавления стыка с помощью критериев подобия (он удобен в применении при достаточно большом количестве основных параметров).

Геометрические размеры зоны проплавления, например, длина сварочной ванны L, является функцией режима и теплофизических свойств материала. Зона проплавления также зависит от геометрической характеристики изделия, например толщины d.

Характерные параметры режима – эффективная мощность источника нагрева, Вт, и скорость сварки, м/с:

η_И – эффективный КПД дуги; V_СВ – скорость сварки, м/с.

Теплофизические свойства материала задаются температурой плавления Т_ПЛ , К; теплопроводностью λ, Вт·м^-1·К; теплоемкостью С, Дж/(кг·К); плотностью ρ, кг/м³.

Искомой величиной является параметр L – длина сварочной ванны, м.

Составим расчетную таблицу.

Режим задан: мощностью источника питания q, Вт, и скоростью сварки V_СВ, м/с.