
Примеры по выводу волновых уравнений.
Р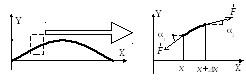 ассмотрим
малые поперечные колебания тонкой
однородной струны длины L
и массы m, закреплённой
с обоих концов. Пусть сила натяжения
струны F постоянная
по величине. Форма проволоки задается
уравнением: y(x).
Выделим малый кусок проволоки, длина
которого вдоль оси X равна
x,
а масса m.
Так как колебания поперечные, то запишем
второй закон Ньютона для куска m
вдоль оси Y:
ассмотрим
малые поперечные колебания тонкой
однородной струны длины L
и массы m, закреплённой
с обоих концов. Пусть сила натяжения
струны F постоянная
по величине. Форма проволоки задается
уравнением: y(x).
Выделим малый кусок проволоки, длина
которого вдоль оси X равна
x,
а масса m.
Так как колебания поперечные, то запишем
второй закон Ньютона для куска m
вдоль оси Y:
![]() .
.
При малых углах (в радианах) справедливо
соотношение:
![]() .
Но:
.
Но:
![]() ,
,
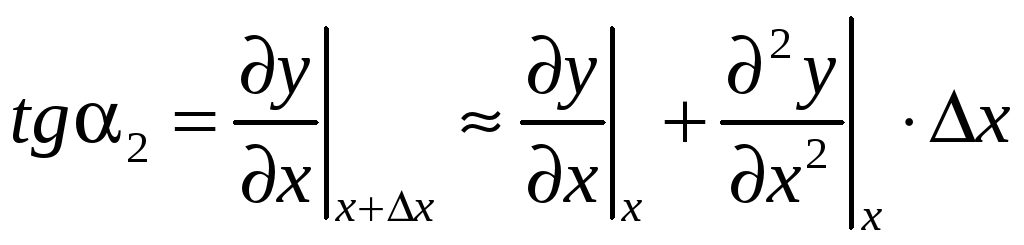 (разложение в ряд Тейлора).
(разложение в ряд Тейлора).
Поэтому:
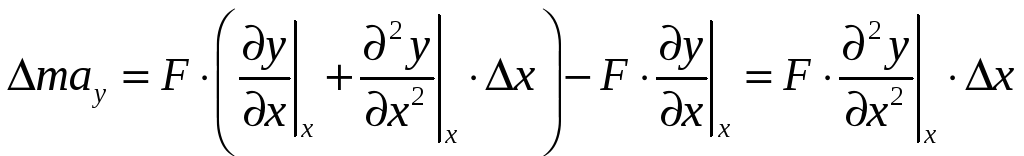 .
.
Т.к.
![]() и
и
![]() ,
то
,
то
 .
Окончательно получаем уравнение:
.
Окончательно получаем уравнение:
![]() .
Поэтому скорость волны в струне:
.
Поэтому скорость волны в струне:
![]() .
.
Е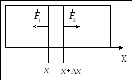 сли
возвращающая сила пропорциональна
смещению точки от положения равновесия,
то волна называется упругой.
Выведем волновое уравнение на примере
продольных волн деформации в стержне.
сли
возвращающая сила пропорциональна
смещению точки от положения равновесия,
то волна называется упругой.
Выведем волновое уравнение на примере
продольных волн деформации в стержне.
Выделим часть стержня длиной x.
Если площадь поперечного сечения стержня
равна S, плотность
материала , то масса
этой части
![]() .
При деформациях на эту часть стержня
действуют силы упругости. Запишем второй
закон Ньютона – уравнение движения
этой части стержня вдоль оси Х:
.
При деформациях на эту часть стержня
действуют силы упругости. Запишем второй
закон Ньютона – уравнение движения
этой части стержня вдоль оси Х:
![]() .
.
Это уравнение записано в предположении
растяжения этой части стержня. Силы
с обеих сторон выделенной части вызваны
деформацией стержня. При равновесии и
отсутствии деформации положение точек
в двух близко расположенных сечениях
стержня можно задать координатами x
и x+x.
При деформировании стержня его точки
сместятся от равновесных положений.
Пусть x1(x)
– задаёт положение точки стержня при
деформации, если её равновесное положение
задавалось координатой x.
Тогда для близкого сечения новыми
координатами будут x1+x1.
Изменение линейного размера части
стержня вызвано смещением точек стержня.
Введём величину смещения: =
x1
x. По определению,
относительная деформация в данном
сечении стержня – это отношение изменения
длины части стержня к начальной длине
этой части:
![]() .
Если стержень сжимается, то его продольные
размеры уменьшаются:
.
Если стержень сжимается, то его продольные
размеры уменьшаются:
![]() и поэтому < 0.
Таким образом, при сжатии
< 0 и при растяжении
> 0.
и поэтому < 0.
Таким образом, при сжатии
< 0 и при растяжении
> 0.
Если все точки стержня смещаются на
одинаковую величину, то изменения длины
участка стержня не происходит. Поэтому
деформация равна разности смещений
соседних точек
![]() .
Тогда можно записать:
.
Тогда можно записать:
![]() .
В пределе (при
.
В пределе (при
![]() )
получаем:
)
получаем:
![]() .
С учётом напряжений в сечениях стержня:
.
С учётом напряжений в сечениях стержня:
![]() ,
,
![]() .
Напряжения в сечениях стержня найдем
по закону Гука:
.
Напряжения в сечениях стержня найдем
по закону Гука:
![]() ,
,
![]() ,
где Е – модуль упругости материала
(модуль Юнга).
,
где Е – модуль упругости материала
(модуль Юнга).
Относительная деформация меняется
вдоль стержня, поэтому можно считать,
что
![]() (разложение в ряд Тейлора).
(разложение в ряд Тейлора).
Ускорение точек выделенной части
стержня:
![]() .
Последовательно подставим эти соотношения
в уравнение движения:
.
Последовательно подставим эти соотношения
в уравнение движения:
![]() ,
т.е.
,
т.е.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
С учетом равенства
![]() ,
после сокращений, получаем дифференциальное
уравнение, описывающее распространение
волны (вдоль одного направления – оси
Х):
,
после сокращений, получаем дифференциальное
уравнение, описывающее распространение
волны (вдоль одного направления – оси
Х):
![]() или
или
![]() .
.
Здесь, - параметр,
описывающий колебания (величина смещения
точек при деформации),
![]() – скорость волны.
– скорость волны.
Рассмотрим выделенный участок стержня
длиной x.
При колебаниях скорость этого участка
![]() и величина деформации
и величина деформации
![]() .
Соответственно, кинетическая и
потенциальные энергии выделенного
участка равны:
.
Соответственно, кинетическая и
потенциальные энергии выделенного
участка равны:
![]() и
и
![]() .
Объём участка:
.
Объём участка:
![]() .
Объёмная плотность механической энергии:
.
Объёмная плотность механической энергии:
![]() .
.
Если уравнение движения волны записать
в виде:
![]() ,
то с учётом соотношений для скорости:
,
то с учётом соотношений для скорости:
![]() и деформации:
и деформации:
![]() получается
получается
![]() или
или
![]() .
.
Используем выражение для скорости
волны:
![]() :
:
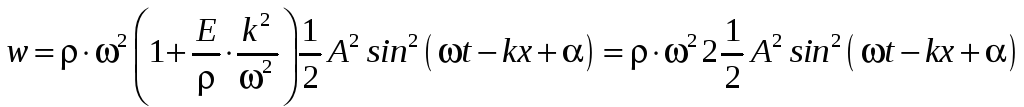 ,
,
![]() .
.
Среднее значение плотности потока энергии, переносимой волной, равно:
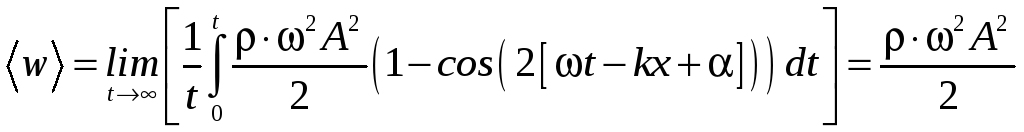
Следствия.
-
Величины скорости точек
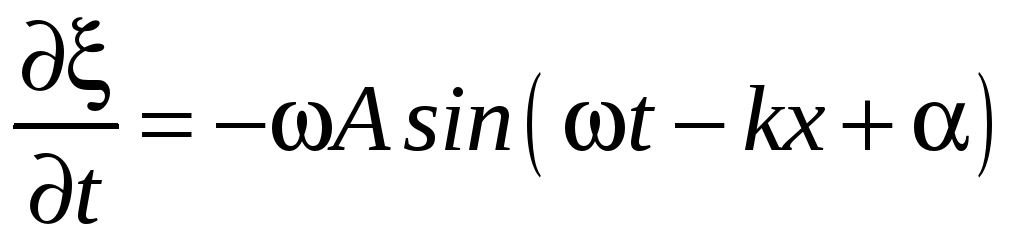 и деформации среды
и деформации среды
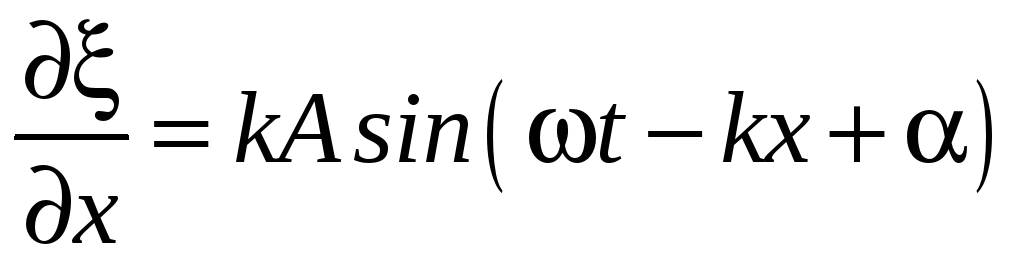 колеблются синфазно
друг другу.
колеблются синфазно
друг другу. -
Закон изменения плотности потока энергии описывается волновым уравнением и представляет волну плотности энергии. Скорость этой волны:
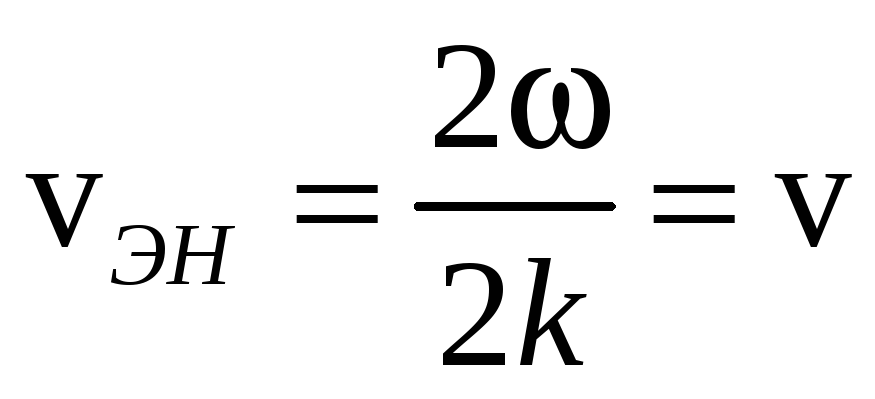 в данном случае совпадает с фазовой
скоростью волны. (В общем случае это не
так.)
в данном случае совпадает с фазовой
скоростью волны. (В общем случае это не
так.)
Вектор Умова
П усть
энергия переносится со скоростью
усть
энергия переносится со скоростью
![]() в направлении под углом
к нормали некоторой малой площадки S.
Тогда вся энергия, прошедшая через эту
площадку за малое время dt
окажется в области, объём которой
равен:
в направлении под углом
к нормали некоторой малой площадки S.
Тогда вся энергия, прошедшая через эту
площадку за малое время dt
окажется в области, объём которой
равен:
![]() (на рисунке эта область является косым
цилиндром). Если объёмная плотность
энергии равна w, то энергия
этого объёма:
(на рисунке эта область является косым
цилиндром). Если объёмная плотность
энергии равна w, то энергия
этого объёма:
![]() .
.
Мощность переноса энергии через площадку S:
![]() .
.
Введём вектор плотности потока энергии (Вектор Умова):
![]() ,
,
тогда
![]() .
Если ввести вектор
.
Если ввести вектор
![]() ,
направленный по нормали к площадке, и
скалярное произведение
,
направленный по нормали к площадке, и
скалярное произведение
![]() определить как поток вектора Умова
через площадку S, то
мощность переноса энергии
через площадку определяется потоком
вектора Умова через эту площадку:
определить как поток вектора Умова
через площадку S, то
мощность переноса энергии
через площадку определяется потоком
вектора Умова через эту площадку:
![]() .
.
Интенсивность волны – это средняя по времени энергия, переносимая волной через площадку в направлении перпендикулярном к этой площадке.
Для плоской волны интенсивность
![]() не меняется при распространении волны.
не меняется при распространении волны.
Для сферической волны интенсивность через любую сферу радиуса R с центром в источнике:
![]()
является постоянной величиной.
Если интенсивность волны при её распространении уменьшается, то среда называется диссипативной. Если интенсивность волны увеличивается, то среда называется активной.
Интерференция волн
Интерференция волн – взаимное усиление или ослабление волн при их наложении друг на друга (суперпозиции волн при одновременном распространении в пространстве), что приводит к перераспределению энергии колебаний, устойчивому во времени. Интерференция волн наблюдается согласно принципу суперпозиции волн.
Р ассмотрим
суперпозицию двух волн одного направления
ассмотрим
суперпозицию двух волн одного направления
![]() и
и
![]() .
.
Воспользуемся амплитудно-векторной диаграммой.
По теореме косинусов:
![]()
Учтем, что
![]() ,
,
![]() ,
тогда
,
тогда
![]() .
.
Если результирующая амплитуда не зависит
от времени, то разность
фаз волн должна быть постоянной во
времени. Такие волны называются
когерентными. В частности,
получаем, что частоты
когерентных волн совпадают:
![]() .
.
Вообще говоря, волны могут двигаться к точке встречи в разных средах, поэтому их скорости могут быть там различными, а также расстояния до точки тоже могут быть разными, поэтому следует написать:
![]() .
.
Поэтому в точке наблюдения может быть:
либо усиление колебаний при
![]() ,
,
либо ослабление колебаний при
![]() .
.
