Свойства плотности распределения вероятностей
Свойство 1. Значения плотности распределения вероятностей есть неотрицательные числа
.
Свойство 2. Вероятность того, что случайная величина X примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения вероятностей в указанных пределах
. (8.5)
Геометрический смысл. Вероятность попадания в интервал для непрерывной случайной величины определяется как площадь, ограниченная графиком функции плотности распределения на заданном отрезке оси Ox.
Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины равно несобственному интегралу
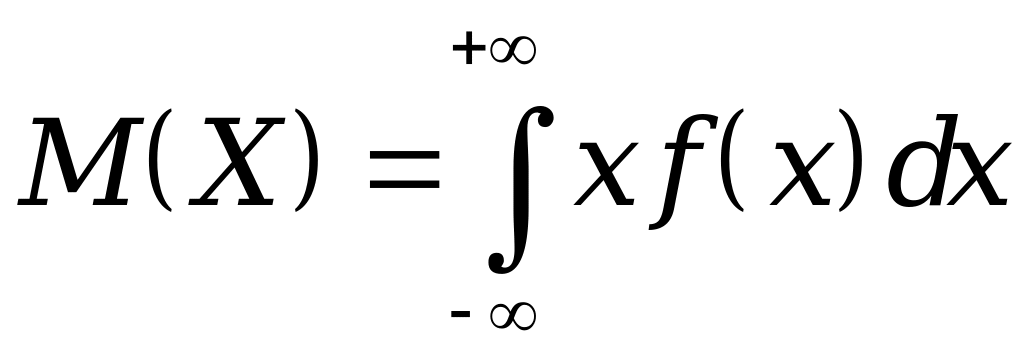. (8.6)
Все свойства математического ожидания, указанные для дискретных случайных величин, сохраняются и для непрерывных.
Дисперсия непрерывной случайной величины определяется как
. (8.7)
Для вычисления дисперсии непрерывной случайной величины также применима формула
. (8.8)
Все свойства дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных.
Замечание.
Если
для всех
,
то интегралы в формулах (8.6)–(8.8) берутся
по
.
Вопросы для самопроверки
1. Что называют дифференциальной и интегральной функциями распределения? Перечислите свойства указанных функций.
2. Как найти математическое ожидание и дисперсию непрерывной случайной величины?
3. Как
вычислить вероятность попадания в
интервал
для непрерывной случайной величины?
Задание
12. В задачах
12.1–12.30 непрерывная случайная величина
X
задана с помощью интегральной функции
распределения
.
Требуется: а)
найти дифференциальную функцию
распределения
случайной величины X;
б)
найти математическое ожидание
и дисперсию
случайной величины X;
в)
вычислить и изобразить геометрически
вероятность попадания случайной величины
X
в заданный интервал
;
г) построить
графики функций распределения
и
.
12.1. 
= –2; 
= 2.
12.2. 
= –1;
= 1.
12.3. 
= –2;
= 1.
12.4. 
= –2;
= 1.
12.5. 
= –5;
= 1.
12.6. 
= –1/2;
= 1/2.
12.7. 
= –4;
= 3.
12.8. 
= –2;
= 4.
12.9. 
= –1;
= 3.
12.10. 
= –2;
= 2.
12.11. 
= –1;
= 2.
12.12. 
= –1;
= 1.
12.13. 
= –2;
= 2.
12.14. 
= –2;
= 5.
12.15. 
= –5;
= 5.
12.16. 
= –2;
= 2.
12.17. 
= –1;
= 1.
12.18. 
= –2;
= 3.
12.19. 
= –3;
= 2.
12.20. 
= –1;
= 1.
12.21. 
= –2;
= 3.
12.22.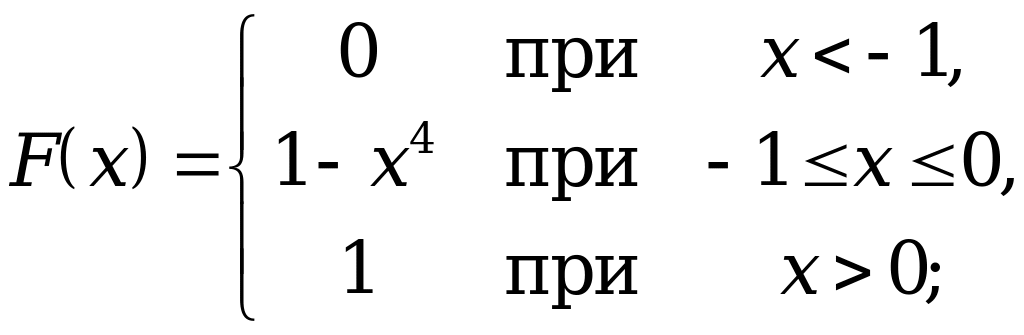 
= –1/5;
= 2/5.
12.23. 
= –1;
= 2.
12.24.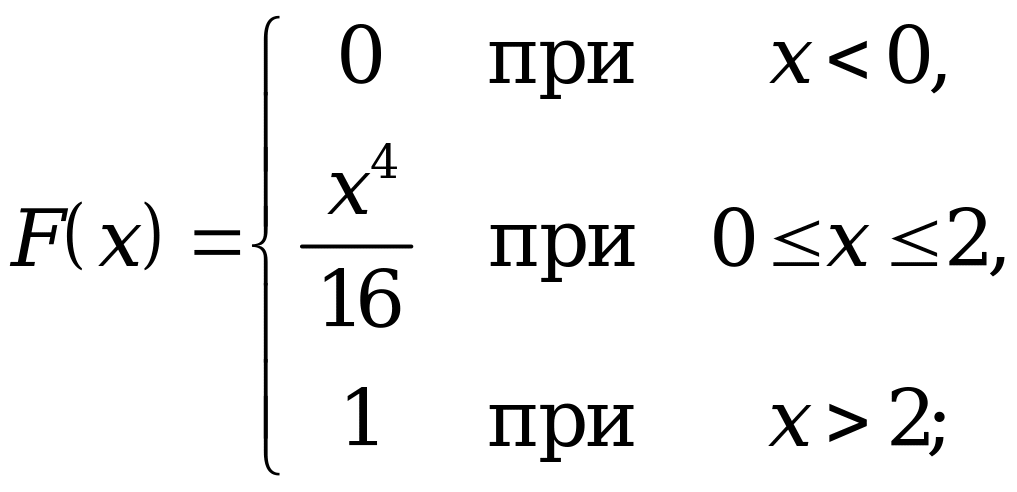 
= –1;
= 1.
12.25. 
= –3;
= 3.
12.26. 
= –1/2;
= 1/2.
12.27.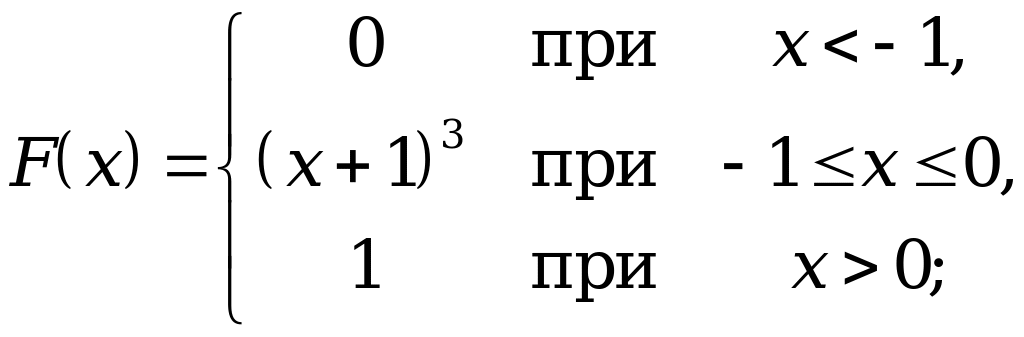 
= –5/3;
= –2/3.
12.28. 
= –1/3;
= 4/3.
12.29. 
= 1;
= 2.
12.30. 
= –1/3;
= 2/3.
Решение типовых примеров
Пример 8.2. Непрерывная случайная величина X задана с помощью интегральной функции распределения
Требуется:
а)
найти дифференциальную функцию
распределения
случайной величины X;
б)
найти математическое ожидание
и дисперсию
случайной величины X;
в)
вычислить и изобразить геометрически
вероятность попадания случайной величины
X
в заданный интервал
;
г) построить
графики функций распределения
и
.
Решение.
Дифференциальная
функция распределения
непрерывной случайной величины X
определяется как первая производная
от интегральной функции распределения
.
В нашем случае имеем
Если
дифференциальная функция распределения
всюду, кроме заданного интервала
то математическое ожидание непрерывной
случайной величины X
равно
.
В
нашем случае
,
и формула принимает вид
.
Дисперсию непрерывной случайной величины найдем по формуле
.
Аналогично предыдущему, при , получаем
.
Вероятность попадания в интервал для непрерывной случайной величины определяется как площадь, ограниченная графиком дифференциальной функции распределения на заданном отрезке оси Ox
.
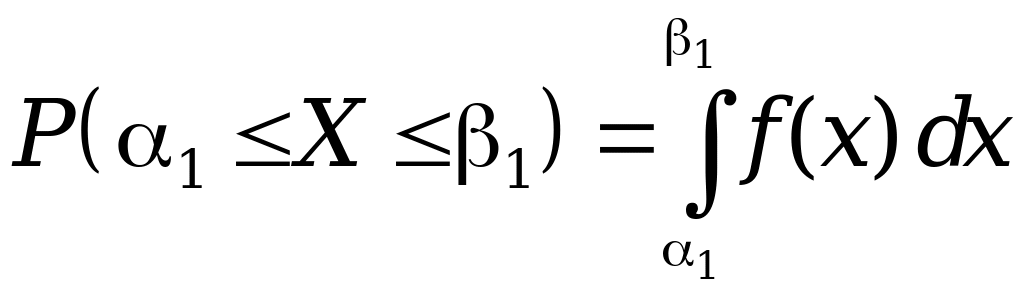Так
как в нашем случае при
дифференциальная функция распределения
равна нулю, то предыдущая формула
принимает вид
.
Построение
графиков функций распределения
и
и геометрическое изображение вероятности
попадания случайной величины X
в заданный интервал
показаны на рис. 8.1.
Рис. 8.1. Графики функций распределения и непрерывной случайной величины X. Пример 8.2