
Решение типовых заданий
ПРИМЕР
1. Даны
координаты вершин треугольника
![]()
![]() .
.
Требуется построить треугольник в системе координат xOy и найти:
длины и уравнения сторон АВ, BC, AC их угловые коэффициенты;
уравнение медианы AE;
внутренние углы треугольника (в градусах, минутах, секундах);
уравнение и длину высоты СD;
уравнение прямой, проходящей через точку E параллельно стороне АВ, и координаты точки М ее пересечения с высотой СD;
площадь треугольника;
уравнение окружности с центром в точке Е, проходящей через точку С.
Решение.
1)
Расстояние
между точками
![]() и
и
![]() определяется по формуле
определяется по формуле
![]() .
(1.1)
.
(1.1)
Назначим
![]() .
Тогда по формуле (1.1) получаем
.
Тогда по формуле (1.1) получаем
![]()
Аналогично:

![]()
![]()
Уравнение прямой, проходящей через две заданные точки плоскости и , имеет вид
![]() (1.2)
(1.2)
Для составления уравнения прямой АВ назначим
,
тогда использование формулы (1.2) дает следующий результат:
 .
.
Полученное уравнение преобразуем сначала к уравнению прямой общего вида Ax+By+C = 0:
![]() .
.
Угловой
коэффициент
![]() прямой
прямой
![]() найдем,
преобразовав ее уравнение общего вида
к виду уравнения прямой с угловым
коэффициентом
найдем,
преобразовав ее уравнение общего вида
к виду уравнения прямой с угловым
коэффициентом
![]() :
:

Аналогично
получим уравнение прямой
![]() и найдем ее угловой коэффициент:
и найдем ее угловой коэффициент:


Теперь займемся прямой АС:


2)
Для составления уравнения медианы
![]() найдем сначала координаты точки
найдем сначала координаты точки
![]() ,
которая лежит на середине отрезка
:
,
которая лежит на середине отрезка
:

Теперь назначим в уравнении (1.2)

и получаем уравнение медианы:
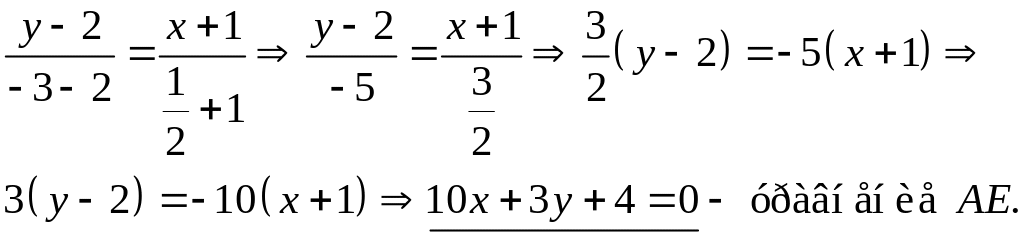
3) Для нахождения внутренних углов треугольника воспользуемся формулами (объясните, почему в числителях этих формул вычитание угловых коэффициентов прямых производится именно в предлагаемых видах):
 (1.3)
(1.3)
Подставив
ранее вычисленные значения
,
![]() и
и
![]() в (1.3), находим:
в (1.3), находим:
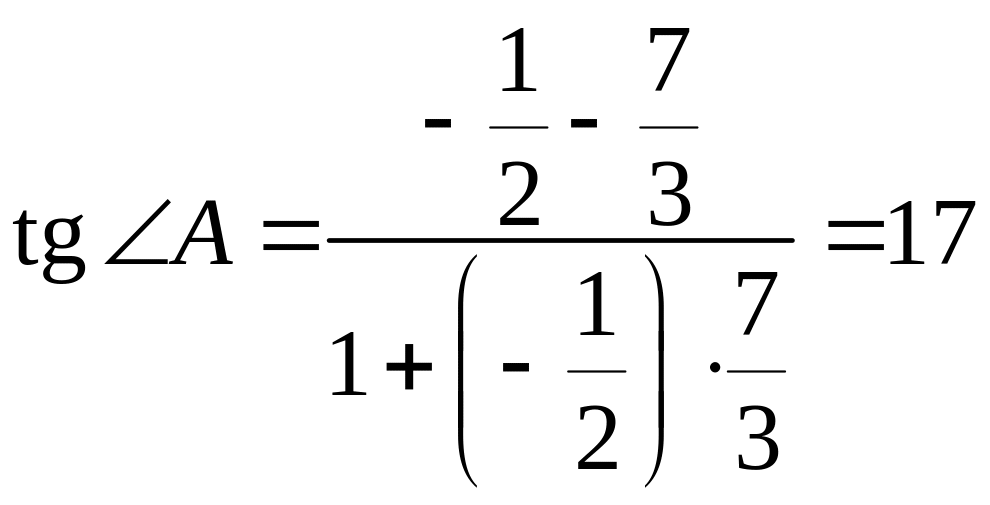 ;
;
 ;
;
 .
.
Теперь, воспользовавшись инженерным микрокалькулятором, получаем
![]()
ПРОВЕРКА:
![]()
4)
Для составления уравнения высоты
![]() воспользуемся уравнением прямой,
проходящей через заданную точку
воспользуемся уравнением прямой,
проходящей через заданную точку
![]() с заданным угловым коэффициентом
с заданным угловым коэффициентом
![]() ,
которое имеет вид
,
которое имеет вид
![]() (1.4)
(1.4)
и
условием перпендикулярности прямых
и
,
которое выражается соотношением
![]() ,
откуда
,
откуда
![]() Подставив в (1.4) вместо
значение
Подставив в (1.4) вместо
значение
![]() ,
а вместо
,
а вместо
![]() соответствующие координаты точки
соответствующие координаты точки
![]() ,
получим уравнение высоты
:
,
получим уравнение высоты
:
![]()
Для вычисления длины высоты найдем сначала координаты точки D пересечения прямых CD и AB, решив систему уравнений этих прямых с помощью формул Крамера:

 .
.
Отсюда по формуле (1.1) имеем

5)
Так как искомая прямая
![]() параллельна прямой
,
то
параллельна прямой
,
то
 .
Подставив в уравнение (1.4) вместо
координаты
точки
,
а вместо
значение
.
Подставив в уравнение (1.4) вместо
координаты
точки
,
а вместо
значение
![]() ,
получаем уравнение прямой
:
,
получаем уравнение прямой
:

Для
отыскания координат точки
![]() решаем
совместно уравнения прямых
и
(по
формулам Крамера!):
решаем
совместно уравнения прямых
и
(по
формулам Крамера!):

Таким
образом,
![]()
6)
Поскольку нам известны величины
![]() и
и
 ,
которые являются соответственно длинами
основания и высоты треугольника, то его
площадь может быть вычислена по формуле
,
которые являются соответственно длинами
основания и высоты треугольника, то его
площадь может быть вычислена по формуле
 (кв.ед.).
(кв.ед.).
7)
Так как окружность имеет центр в точке
![]() и проходит через вершину
и проходит через вершину
![]() ,
то ее радиус
,
то ее радиус

Каноническое
уравнение окружности радиуса R
с центром в точке
![]() имеет вид
имеет вид
![]()
В нашем примере получаем

Треугольник
,
высота
![]() ,
медиана
,
медиана
![]() ,
прямая
,
точка
,
прямая
,
точка
![]() и окружность изображены в системе
координат
и окружность изображены в системе
координат
![]() на рис. 1.1.
на рис. 1.1.

Рис. 1.1
