
5585
.pdf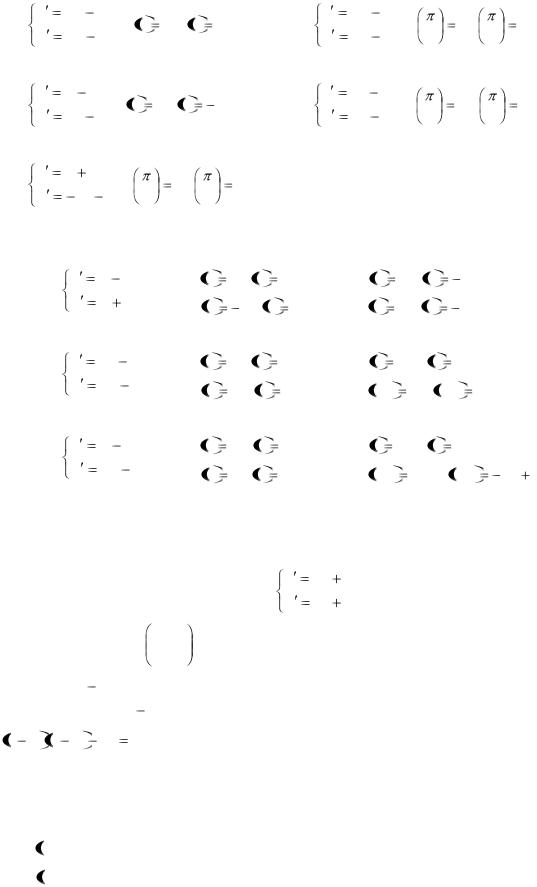
11) |
x |
2x |
5y |
|
x 0 |
|
6, y 0 |
7 ; |
12) |
x |
2x |
y |
x |
|
|
|
1, y |
|
|
1; |
|||||
y 6x 9 y; |
|
y 5x 2 y; |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||||||||||||
13) |
x |
x |
y |
|
x 0 |
1, y 0 |
1; |
14) |
x |
3x |
5y |
x |
|
|
0, y |
|
|
3 ; |
|||||||
y 5x y; |
y 5x 3y; |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
8 |
|
|
|||||||||||
15) |
x |
x |
2 y |
|
x |
|
|
1, y |
|
5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
5x |
y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ДС4. Найдите общее и частное решение: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) |
x x y |
|
а) x 0 1, y 0 0 ; |
|
в) x 0 2, y 0 |
3; |
|
|
|
|
||||||||||||||
|
y |
|
x |
|
3y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
б) x 0 |
1, y 0 0 ; |
|
г) x 0 0, y 0 |
1; |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2) |
x |
|
3x |
|
2 y |
|
а) x 0 |
1, y 0 |
0 ; |
|
в) x 1 |
2e, y 1 |
1,5e ; |
|
|
|||||||||
|
y |
|
2x |
|
y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
б) x 0 0, y 0 1 ; |
|
г) x ln3 3, y ln3 3; |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3) |
x |
|
x 2 y |
|
а) x 0 3, y 0 2 ; |
|
в) x 1 2e, y 1 e ; |
|
|
|||||||||||||||
|
y |
|
2x |
3y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
б) x 0 |
1, y 0 |
1; |
|
г) x ln2 |
ln2, y ln2 |
|
0,5 ln2 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Другие способы решения систем ЛДУПК
Пусть по-прежнему дана система |
x |
ax |
by , где a, b, c, d – известные числа. |
|||||||||
|
|
|
|
|
|
|
|
|
y |
cx |
dy |
|
Составим матрицу |
a |
b |
и найдем её собственные числа k, при которых опре- |
|||||||||
c |
d |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
делитель |
|
a |
k |
b |
|
|
равен 0. Как известно, для этого надо решить уравнение |
|||||
|
|
|
||||||||||
|
|
|
c |
d k |
|
|
|
|
|
|
||
a k d |
k |
bc |
0 , сводящееся к квадратному. Получим корни k1, k2 . |
|||||||||
В зависимости от знака дискриминанта возможны 3 тех же случая, что при решении обычного линейного ДУ с постоянными коэффициентами (см. § 14). Соответственно, по этим корням составляем общие решения:
x t  с постоянными C1 , C2 ; y t
с постоянными C1 , C2 ; y t с постоянными C3 , C4 ,
с постоянными C3 , C4 ,
после чего остаётся выяснить, как C3 , C4 зависят от C1 , C2 (или наоборот).
102

Очевидно, все 4 постоянные надо подобрать так, чтобы выполнялись уравнения системы. Для этого находим производные от x t  и y t
и y t и вместе с функциями подставляем в условие задачи.
и вместе с функциями подставляем в условие задачи.
Пример 5. Решим систему |
x |
|
4x |
3y |
. Её матрица A |
4 |
3 |
, а характе- |
|||
|
y |
|
6x |
7 y |
|
|
|
6 |
7 |
|
|
ристическое уравнение имеет вид |
|
k |
3 |
|
0 . |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||
|
|
6 |
7 |
k |
|
|
|
|
|
|
|
Раскрыв определитель, видим, что |
4 |
k |
7 k 3 6 0 , или k 2 |
11k 10 0 . |
|||||||
|
|
|
|
|
|
|
x t C et |
|
C |
e10t |
|
Корни уравнения – числа k1 |
1 и k2 |
10 . Значит, |
1 |
|
2 |
|
. |
||||
y t C3et |
|
C4 e10t |
|||||||||
|
|
|
|
|
|
|
|
|
|||
Посмотрим, как связаны между собой постоянные C. Найдём производные
x t C1et 10C2 e10t
y t C3et 10C4 e10t
и подставим их, а также x t  и y t , в условие задачи. Получим систему
и y t , в условие задачи. Получим систему
C et |
10C |
e10t |
4 C et |
C |
e10t |
3 C |
et |
C |
e10t |
|
|
1 |
|
2 |
|
1 |
2 |
|
3 |
|
4 |
|
, |
C |
et |
10C |
e10t |
6 C et |
C |
e10t |
7 C |
et |
C |
e10t |
|
3 |
|
4 |
|
1 |
2 |
|
3 |
|
4 |
|
|
и в ней соберём слева слагаемые с et , а справа – слагаемые с e10t :
C et |
4C et |
3C |
et |
|
|
10C |
e10t |
4C |
|
e10t |
3C |
e10t |
|
||||
1 |
|
1 |
3 |
|
|
|
2 |
|
|
|
2 |
|
4 |
|
|
, |
|
C |
et |
6C et |
7C |
et |
|
|
10C |
|
e10t |
6C |
|
e10t |
7C |
|
e10t |
||
3 |
|
1 |
3 |
|
|
|
4 |
|
|
|
2 |
|
4 |
|
|
||
или, что то же самое, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3C 3C |
3 |
et |
6C |
2 |
3C |
4 |
e10t |
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
e10t . |
|
|
|
|
|||
|
|
6C 6C |
3 |
et |
|
3C |
4 |
6C |
2 |
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
Но et и e10t – разные функции, а равенство должно выполняться при всех t. Это возможно, только когда коэффициенты перед et и e10t обращаются в 0:
3C1 |
3C3 |
0 è |
6C2 |
3C4 |
0 |
6C1 |
6C3 |
0 è |
3C4 |
6C2 |
0 . |
Заметим, что 2-я строка дублирует 1-ю – это говорит о том, что все действия до сих пор выполнялись верно. При внимательном решении достаточно подставить производные в одно уравнение. Итак,
3C1 |
3C3 |
0 |
3C1 |
3C3 |
C3 |
C1 |
6C2 |
3C4 |
0 |
6C2 |
3C4 |
C4 |
2C2 |
103
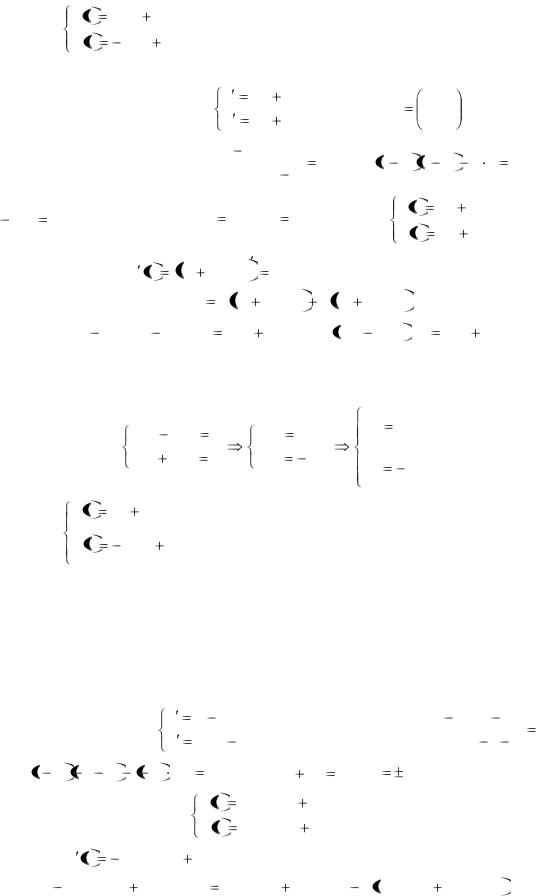
(как обычно, выразили C3 , C4 |
через C1 , C2 ). |
|
|
|
|
|
|
|
|
||||||||||||||
|
x t |
C et |
C |
e10t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y t |
C et |
2C |
e10t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6. Решим систему |
|
x |
2x |
|
6 y |
. Матрица A |
2 |
6 |
приводит к ха- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
3x |
|
9 y |
|
|
|
|
3 |
9 |
|
|
|
рактеристическому уравнению |
|
2 k |
|
6 |
|
0 , т.е. |
2 |
|
k 9 |
k |
6 3 0 , откуда |
||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
9 |
|
k |
|
|
|
|
|
|
|
|
k 2 11k 0 и соответственно k |
|
|
0 и k |
|
|
11. Поэтому |
x t |
C |
C |
e11t |
|||||||||||||
|
|
2 |
|
|
|
1 |
2 |
. |
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
y t |
C3 |
C4 e11t |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теперь находим x t |
|
C |
|
C |
e11t |
|
11C |
e11t и подставляем в 1-е уравнение: |
|||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
11C |
e11t |
|
2 C C |
e11t |
6 C C |
e11t |
, |
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
2 |
|
|
3 |
4 |
|
|
|
|
|
|
откуда 11C e11t |
2C |
e11t |
6C |
e11t |
|
|
2C |
6C |
или 9C |
6C |
4 |
e11t |
2C |
6C . |
|||||||||
|
2 |
2 |
|
|
|
4 |
|
|
|
|
1 |
|
|
3 |
|
2 |
|
|
|
1 |
|
3 |
|
По той же причине, что и в примере 5, приравниваем к 0:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C4 |
3 |
C2 |
|
|
|
|
|
|
|
|
|
|
9C2 |
|
6C4 |
|
0 |
|
9C2 |
6C4 |
2 |
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2C1 |
|
|
6C3 |
|
0 |
|
2C1 |
6C3 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
C3 |
C1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
x t |
C |
|
C |
2 |
e11t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: |
y t |
|
1 |
C |
|
|
3 |
C |
e11t . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Замечание. В примере 6 столбец коэффициентов перед C1 |
– это собственный |
|||||||||||||||||||||||
вектор для числа 0. Столбец перед C2 – собственный вектор для числа 11. По- |
||||||||||||||||||||||||
добное свойство выполнено и в примере 5. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пример 7. Система |
|
x |
|
x |
5y |
|
приводит к уравнению |
|
k |
5 |
|
0 , по- |
||||||||||||
|
|
|
1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
3,4x |
y |
|
|
|
|
|
|
3,4 |
1 |
k |
|
||||
этому 1 k |
1 |
k |
|
5 |
3,4 |
|
0 . Тогда k 2 |
16 0 и k |
4i . Для таких корней |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x t |
C1 cos4t |
C2 sin 4t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y t |
C3 cos4t |
C4 sin 4t . |
|
|
|
|
|
|
|
|
|||
Найдём x t |
4C1 sin 4t 4C2 cos4t и подставим в 1-е уравнение: |
|
|
|
||||||||||||||||||||
|
4C1 sin 4t |
|
4C2 cos4t |
C1 cos4t C2 sin 4t 5 C3 cos4t |
|
C4 sin 4t . |
|
|
||||||||||||||||
104
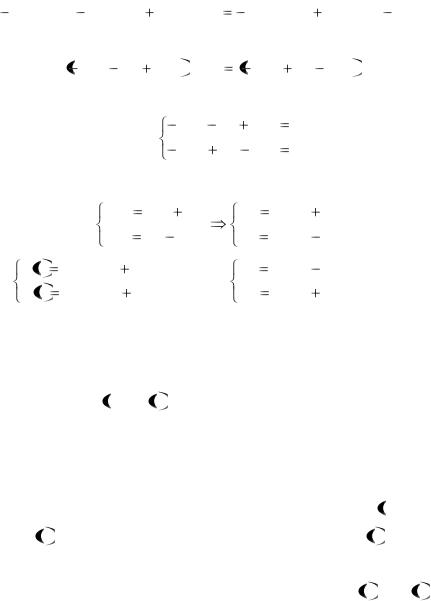
Группируем:
|
4C1 sin 4t C2 sin 4t |
5C4 sin 4t |
|
4C2 cos4t |
C1 cos4t 5C3 cos4t , |
|||||
что равносильно равенству |
|
|
|
|
|
|
|
|||
|
|
4C1 C2 |
5C4 |
sin 4t |
|
4C2 |
C1 |
5C3 cos4t . |
||
Снова должно выполняться условие |
|
|
|
|
||||||
|
|
|
|
|
4C1 |
C2 |
5C4 |
0 |
|
|
|
|
|
|
|
4C2 |
C1 |
5C3 |
0. |
|
|
Нас интересует, как C3 , C4 |
выразить через C1 , C2 , поэтому находим, что |
|||||||||
|
|
5C4 |
|
4C1 |
C2 |
|
C4 |
0,8C1 |
0,2C2 . |
|
|
|
5C3 |
|
C1 |
4C2 |
|
C3 |
0,2C1 |
0,8C2 . |
|
Ответ: |
x t |
C1 cos4t |
C2 sin 4t , где |
C3 |
0,2C1 |
0,8C2 . |
||||
|
y t |
C3 cos4t |
C4 sin 4t |
|
C4 |
0,8C1 |
0,2C2 |
|||
Замечание. Решение системы линейных ДУ с постоянными коэффициентами фактически распадается на 2 независимые задачи:
а) поиск функций x t  и y t ;
и y t ;
б) поиск зависимости между постоянными.
В пособии даны 2 способа решения каждой из этих задач. Тем самым получается (без учёта других способов) 4 пути решения. Например, можно:
а) найти функции через собственные числа и выразить y t из 1-го уравнения; б) найти x t , методом подстановки избавившись от y t , а зависимость кон-
из 1-го уравнения; б) найти x t , методом подстановки избавившись от y t , а зависимость кон-
стант – как в примерах 5 – 7, и т.д.
Более того, можно методом подстановки искать не x t , а y t ; можно выражать не C3 , C4 через C1 , C2 , а наоборот. Тем самым система ЛДУПК даже 2-го порядка допускает множество способов решения. Для систем же 3-го порядка и выше возможны самые разнообразные пути решения.
Поиск частного решения при каких-либо условиях никак не зависит от того, каким образом найдено общее решение.
ДС5 – ДС8. Решите какие-либо системы (по собственному выбору), предложенные в заданиях ДС1 – ДС4, так, как в примерах 5 – 7. Сравните ответы. Затем примените для решения разные комбинации способов, сравните их трудоёмкость и простоту.
105
