
681_Trofimov_V.K._Teoremy_kodirovanija_neravnoznachnymi_
.pdf
Теорема 4.3.1. Для средней избыточности универсального кодирования множества источников 0 справедливо асимптотическое неравенство
|
|
N, |
|
|
|
|
k 1 |
|
log N |
. |
(4.16) |
||
|
|
||||||||||||
|
R |
, |
t |
|
|||||||||
|
|
|
|
|
|
||||||||
0 |
|
Y |
|
2C tY |
|
N |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Доказательство. Как следует из основной теоремы К. Шеннона [28],
правая часть (4.16) достигает своего минимума при кодировании
|
|
1 (w) log 0 |
p(wi ) |
|
1 |
|
log p(wi ) , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
C(tY ) |
|||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Откуда в силу (4.15) следует соотношение |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
R N, 0 , tY |
|
|
|
f ( )R N, , , t1 d . |
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
tY 0 |
|
|
|
|
|
|
|
|
||||||||
Из последнего неравенства и из [22, 63] получаем |
|
|
|||||||||||||||||||||||||||
|
|
|
|
N, |
, |
|
|
|
k 1 |
|
log N |
. |
Теорема доказана. |
||||||||||||||||
|
|
R |
|
||||||||||||||||||||||||||
|
|
|
t |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
0 |
|
Y |
|
|
2C tY |
|
|
N |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4.4.Асимптотика избыточности универсального кодирования множества бернуллиевских источников
Теорема 4.4.1. Для избыточности универсального кодирования множе-
ства источников без памяти 0 буквами выходного алфавита с неравнознач-
ными длительностями символов справедливо асимптотическое равенство
R N, |
|
|
k 1 |
|
log N |
. |
(4.17) |
||||
, |
t |
|
|||||||||
|
|
|
|
|
|||||||
0 |
|
Y |
|
2C tY |
|
N |
|
||||
|
|
|
|
|
|
|
|||||
Доказательство. Оценка сверху следует из (4.13).
В самом деле, из теоремы 4.2.1 имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
** |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
log N |
|
|
|
t |
|
T(k) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
N , , |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
r |
|
|
, t |
|
|
|
|
. |
(4.18) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 , p |
|
Y |
|
2C tY |
|
|
|
N |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Неравенство (4.18) справедливо при любом законе распределения вероят-
ностей p , величины t** и T(k) ограничены. Правая часть не зависит от закона распределения p , следовательно, из соотношения (2.29) получаем, что
51

|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
** |
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
log N |
|
|
|
t |
|
T(k) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
N , , |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
. (4.19) |
|||
sup r |
|
|
, t |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
0 , p |
|
Y |
|
2C tY |
|
|
|
N |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Так как по определению 1.16
R N, , tY sup r N, , 0 , p , tY ,
0
то из (4.19) следует верхняя оценка для R N, 0 , tY .
Справедливость нижней оценки вытекает из определения (4.15), неравен-
ства R N, 0 , tY R N, 0, tY и (2.27).
Теорема доказана.
Пример 1. Кодирование блоков длины 3 при различных длительностях кодовых символов. Значения КТ-распределения в этом случае равны
Рассмотрим процедуру кодирования в бинарный алфавит при все более разли-
чающихся длительностях символов кодового алфавита и фиксированной длине входных слов N=3.
Рис. 12
52

Соответственно, кодовые слова и их длительности:
Рис. 13.
53
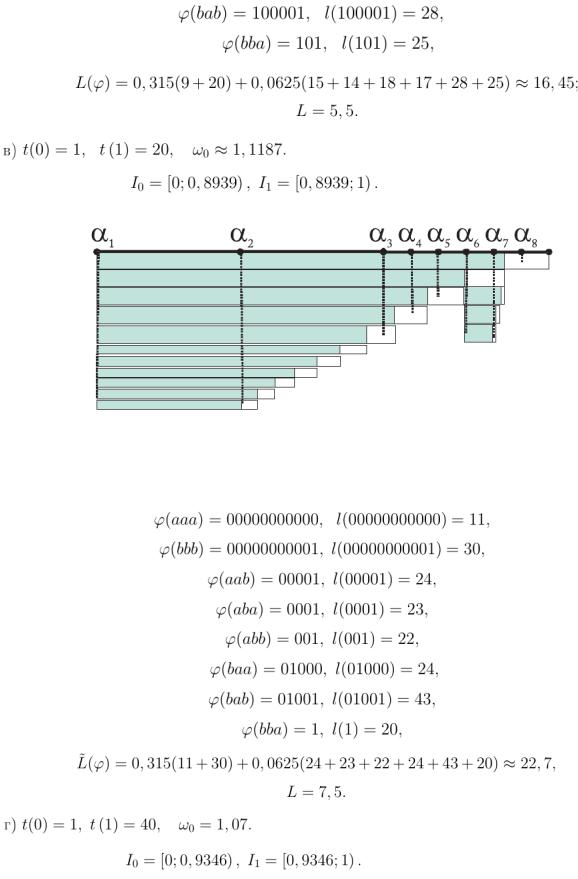
Рис. 14.
54
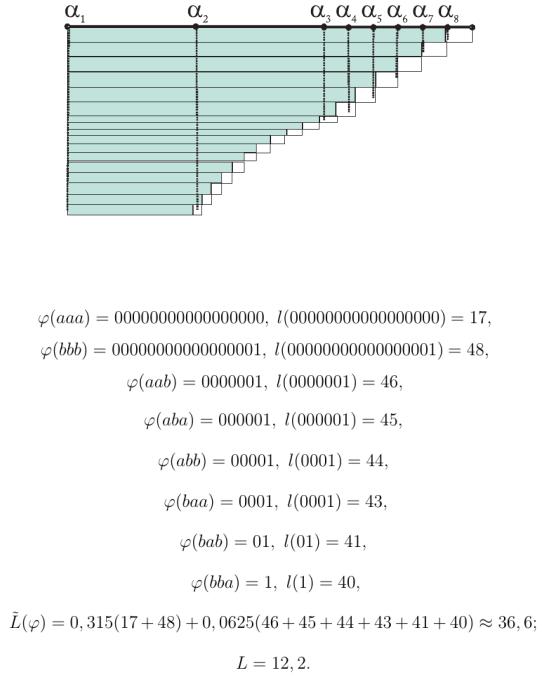
Рис. 15.
Как легко заметить, чем больше разница в длительностях букв, тем боль-
шая часть интервала отводится для более «дешевого» кодового символа. К тому же, КТ-вероятности появления слов, попадающих в правую, более «дорогую» часть интервала существенно меньше слов из левой части.
С ростом длины входного блока растет и количество всевозможных вход-
ных последовательностей. В правой части интервала (с более «дорогими» кодо-
выми символами) точки, соответствующие значениям wi , расположены бо-
лее густо, их количество составляет большую часть от 2N, но и КТ-вероятности
55

этих слов очень малы по сравнению со словами wi , которым соответствуют точки из левой части интервала [0;1).
Пример 2. Кодирование блоков длины 4 при различных длительностях кодовых символов.
Рис. 16.
56
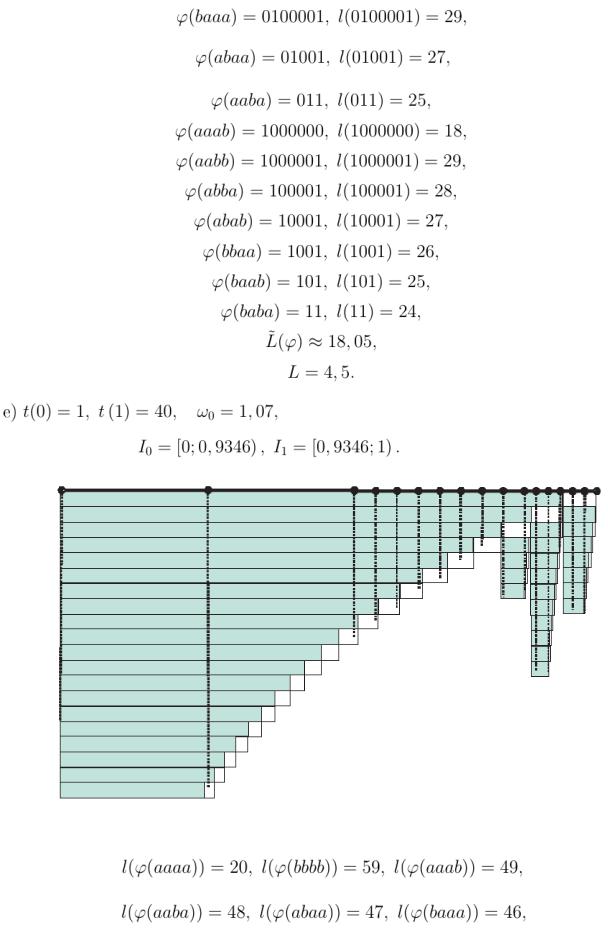
Рис. 17.
57

5.Универсальное кодирование марковских источников буквами кодового алфавита с неравными длительностями
5.1.Кодирование неравнозначными символами информации, порожденной неизвестным марковским источником
Множество всех марковских источников порядка s обозначим как s .
Рассмотрим произвольный марковский источник s с входным алфавитом
X x1, x2 ,..., xk . Вероятность появления любой буквы алфавита в сообщении марковского источника определяется ее s предшествующими. Таким образом,
для марковского источника вероятность появления некоторого слова (блока)
w X N вида wi xi xi |
xi |
xi |
s 1 |
xi |
N |
|
определяется вектором вероятностей |
||||||||||
i |
|
1 |
2 |
s |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
w0 |
|
|
|
|
|
|
|
|
|
|
|
|
начальных блоков |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
pw0 p w0 |
0 |
X |
s |
(5.1) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
|
||
и k s k матрицей |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
P pvi v X *,i |
|
, |
|
(5.2) |
|||||||
|
|
|
|
|
|
1,k |
|
||||||||||
где pvi p xi |
|
v – условная вероятность появления буквы xi |
после блока v. |
||||||||||||||
|
|||||||||||||||||
|
Введем следующие обозначения: |
|
|
|
|
|
|
|
|
|
|||||||
n n |
w – число вхождений буквы |
x в блок w X N ; |
|
||||||||||||||
i |
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
n |
n |
w – число вхождений буквы x |
i |
после блока v X s ; |
(5.3) |
||||||||||||
vi |
vi |
|
|
|
|
|
|
|
|
|
|
|
|
||||
nv nv w nvi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
xi X |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Тогда для вероятности |
ps w |
появления слова w X N на выходе источ- |
||||||||||||||
ника s имеет место равенство
58

k |
|
ps w pw0 pvini , |
(5.4) |
v X * i 1
pw0 – вероятность префикса w0 X s блока w X N согласно (5.1).
Асимптотически точное значение для избыточности универсального
блочного кодирования множества марковских источников порядка s в алфавит с равными длительностями получено В.К. Трофимовым в работе [19], где дока-
зано, что
|
|
|
k s |
|
k 1 |
|
|
|
R N, s , t1 |
|
|
|
|
log N |
(5.5) |
||
|
|
2 |
|
N log m |
||||
|
|
|
|
|
|
|
||
Из последнего асимптотического равенства (5.5) при s=0 следует резуль-
тат Р. Е. Кричевского, приведенный в [3]. Верхняя оценка для избыточности универсального блочного кодирования марковского источника порядка s в ал-
фавит с равными длительностями получена Ю. М. Штарьковым в [29].
Из (5.5) и [4] вытекает, что множитель k s k 1 log N служит «платой» за
2log m
незнание источника.
Рассмотрим s – марковский источник порядка s, закон распределе-
ния которого неизвестен. Зададим на множестве X N всех блоков wi X N КТ-
распределение [19]
|
|
|
|
k |
|
|
k s |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p |
s |
(w ) |
2 |
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
i |
|
|
|
k |
|
|
|
|
|
|
|
k 2 |
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
nvi ' |
|
|
|
|
|||
|
|
|
|
|||||
|
i ' 1 |
|
|
|
|
2 |
(5.6) |
|
|
|
k |
|
|||||
v X s |
|
|
||||||
nv |
2 |
|
|
|
||||
|
|
|
|
|
|
|||
где z – гамма-функция и nvi ', nv определены выше.
Следующая лемма позволяет оценить максимальное различие между рас-
пределением источника и КТ-распределением.
Лемма 5.1.1. Для произвольного марковского источника Θ, s , с ал-
фавитом X, |X| = k, и законом распределения ps (w), w X N , с условными веро-
ятностями (5.2), имеет место неравенство:
59
log |
ps |
(w) |
log pw0 |
k s k 1 |
(N, s,k) log(N s) T *(k) |
(5.7) |
|
|
|
|
|||||
|
p |
s |
(w) |
2 |
|
|
|
|
|
|
|
|
|
||
где T *(k) – некоторая постоянная относительно N величина, (N,s,k) 0, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
ps (w) определяется равенством (5.4), а ps |
(w) – равенством (5.6). |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Доказательство. Сравним значения ps |
(w) и ps |
|
(w) . Из (5.4) имеем |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ps (w) pw0 pvjn j (w) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v X s j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Очевидно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
ps (w) |
|
|
|
|
|
|
|
ps (w) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ps (w) |
|
max ps (w) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Максимальное |
значение функции |
|
|
|
ps |
(w) |
|
|
как |
|
функции |
аргументов p (w) , |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vj |
||
j |
|
, v X s , достигается при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1, k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
pvj (w) |
|
nvjnvj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n v |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
max p (w) pw0 |
|
|
|
|
nvjnvj |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v X s |
|
nvnv |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
k |
|
|
|
|
k |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
nvnv |
|
|
|||||||||||||||||||||||||
|
|
|
ps (w) |
|
p s (w) |
|
|
|
|
|
|
|
|
|
|
|
nvj |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 v X s |
|
j 1 |
|
|
|
|
|
|
2 |
|
|
|
v X s |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
ps (w) |
max ps (w) |
|
|
|
s |
|
|
|
k s k |
|
|
|
|
|
|
|
|
k |
|
|
|
0 |
k |
nvj |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
k k |
|
|
2 |
|
|
nv |
|
|
|
|
|
|
pw |
nvj |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v X |
s |
|
|
|
|
|
|
|
|
|
v X s j 1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Логарифмируя и преобразуя последнее неравенство, получим |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ps |
(w) |
|
|
|
s |
|
|
|
k |
s |
|
|
|
|
|
|
|
k s |
k |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
log |
|
|
k |
|
|
log |
|
|
|
|
k |
|
log k |
|
|
|
|
|
|
log |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
ps |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
(w) |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60
