681_Trofimov_V.K._Teoremy_kodirovanija_neravnoznachnymi_

Рис. 2. Схема канала без шума.

Источник сообщений однозначно определяется алфавитом и законом рас-

пределения вероятностей, заданном на символах алфавита. Основной характе-

ристикой источника сообщений является энтропия H. Кодирование источника характеризуется стоимостью L (средним числом кодовых символов, приходя-

щимся на одну букву сообщения источника). Пропускная способность канала

C в рассматриваемом случае полностью определяется кодовым алфавитом Y

(длительности символов которого могут быть как одинаковы, так и различны).

Величина R, определяемая равенством R L H 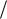C , называется избыточно-

стью кодирования и является показателем его эффективности.

Величины H, L, C и R нуждаются в аккуратных и корректных определе-

ниях, которые, так же как и определение кодирования, будут даны в ближай-

ших секциях.

Если закон распределения неизвестен, источник сообщений также назы-

вается неизвестным и речь идет об универсальном кодировании. Универсальное кодирование впервые рассматривалось в работах А. Н. Колмогорова [2] и

Б. М. Фитингофа [23]. В данной работе рассматривается равномерное по входу универсальное кодирование сообщений источника. Длину сообщения источни-

ка обозначим как N.

1.2. Понятие источника информации

Под источником информации подразумевается некоторое устройство, по-

рождающее по определенному закону сообщения (слова), состоящие из букв некоторого алфавита. Для полного описания источника информации требуется:

–задать входной алфавит;

–задать закон распределения вероятностей появления букв входного ал-

фавита в сообщениях источника.

11

Пусть в дальнейшем X* – множество всех конечных последовательностей,

состоящих из элементов множества X, а Xn – множество всех последовательно-

стей длины n, состоящих из элементов множества X.

Определение 1.2.1. Источник информации Θ представляет собой пару

X , p , где X – некоторый входной алфавит, p : X [0;1] – закон распределе-

ния вероятностей появления букв входного алфавита X в сообщениях источника w X * .

Входной алфавит X x1, x2 ,..., xk может быть как конечным, так и бес-

конечным. Один из частных случаев – бинарный входной алфавит X B 0;1 . В

случае конечного алфавита число букв алфавита X x1, x2 ,..., xk будем обо-

значать как X , X k .

Определение 1.2.2. Закон распределения вероятности появления букв

алфавита X источника Θ в сообщении – это функция

p : X [0;1] , p xi P xi w , w X * .

Определение 1.2.3. Закон распределения вероятности появления слов из букв алфавита X источника Θ – это функция

p : X N [0;1], p w P w , w X * .

Определение 1.2.4. Источник называется неизвестным, если закон рас-

пределения вероятностей появления букв входного алфавита в сообщениях не-

известен.

Среди различных типов источников выделим следующие: бернуллиев-

ский, марковский и стационарный.

Определение 1.2.5. Бернуллиевский источник информации – это источ-

12

Определение 1.2.6. Марковский источник информации порядка s – это

Определение 1.3.2. Энтропия H стационарного источника сообще-

ний Θ с алфавитом X и законом распределения p определяется равенством (см.

[1, 22, 46])

где Hn определена равенством (1.2).

Определение 1.3.3. Энтропия H марковского источника сообщений

Θ с алфавитом X и законом распределения p определяется равенством (см.

[1, 22, 46])

щений Θ с алфавитом X и законом распределения p определяется равенством

(см. [1, 22, 46])

где p xi – вероятность появления буквы xi X на выходе источника Θ.

Очевидно, что если сообщения источника Θ – однобуквенные слова, то энтропия H принимает вид

H H1 p xi log p xi .

xi X

Энтропия источника определяет среднее количество информации в сооб-

щениях источника и является показателем его «непредсказуемости». Макси-

14

Если закон распределения вероятностей принимает вид p x 1,i i '; i 0,i i ',

то значение энтропии минимально: H0 0log 0 1 log1 0 .

Таким образом, имеет место двойное неравенство

0 H log k .

Пусть Θ – источник, порождающий последовательности фиксированной длины N над алфавитом X, X k . Такой источник можно рассматривать как порождающий однобуквенные слова над алфавитом X N . В дальнейшем для ис-

точника, порождающего блоки длины N, будем использовать обозначение N .

Согласно (1.2) имеет место равенство

Определение 1.3.5. Информационной дивергенцией двух законов распре-

деления вероятностей p и q, заданных на одном и том же алфавите X, называет-

ся величина

15

Информационную дивергенцию можно воспринимать как меру «различия» между законами распределения p и q, хотя в общем случае

DX p q DX q p .

1.4. Кодирование источника сообщений

Рассмотрим источник информации Θ с алфавитом X x1, x2 ,..., xk .

Определение 1.4.1. Кодирование сообщений источника в слова кодового алфавита Y y1, y2,..., ym заключается в отображении каждого слова w X *

источника Θ в некоторую последовательность w Y * .

Буквы выходного алфавита Y могут быть как равнозначными по длитель-

ности или стоимости передачи, так и нет. Например, при передаче букв азбукой Морзе мы имеем дело с выходным алфавитом «точка, тире», символы которого не равнозначны, а при кодировании букв алфавита кодом Бодо все буквы кодо-

вого алфавита, состоящего из символов 0 и 1, равнозначны.

Определение 1.4.2. Пусть каждая буква yi Y ( i 1, m) имеет свою стои-

мость передачи, равную t yi ti , i 1, m. Вектор длительностей tY букв кодо-

вого алфавита определяется равенством tY t1,t2 , ,tk . В частности, вектор,

все координаты которого равны 1, будем обозначать как t1 .

Таким образом, каждому кодовому алфавиту Y ставится в соответствие

некоторый вектор длительностей букв tY .

Определение 1.4.3. Равномерное по входу кодирование сообщений источ-

определяется как сумма длительностей входящих в него символов:

16

Очевидно, что при tY t1 длительность (1.10) равна числу букв в кодовом слове: l w , t1 w .

Определение 1.4.5. Средняя длительность кодового слова для блоков длины N, порожденных источником Θ при кодировании и выходном алфа-

вите с вектором tY , определяется равенством

L N, , , tY p w l w , tY . (1.11)

w X N

Определение 1.4.6. Стоимостью L N, , , tY кодирования называется

средняя длительность букв кодового алфавита, приходящаяся на одну букву со-

общения источника. Для стоимости равномерного по входу кодирования, оче-

видно, имеет место равенство

Множество слов называется префиксным, если ни одно слово из этого множе-

ства не является префиксом другого слова.

Например, множество {0,11,10} – префиксное, а {0,1,10} префиксным не является, так как слово 1 является префиксом слова 10.

Определение 1.4.8. Если множество кодовых слов w w X * яв-

ляется префиксным, то называется префиксным кодированием.

Для любого кодирования гарантией однозначного декодирования явля-

ется префиксность. Имеет место следующая теорема (см. [22, 48, 53]).

17

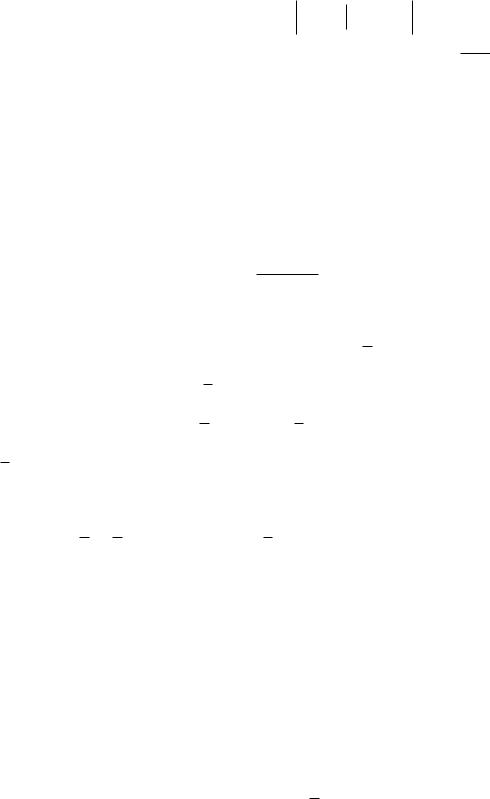
Неравенство Крафта. Для того чтобы кодирование являлось однозначно де-

кодируемым, необходимо и достаточно выполнения неравенства

M

m li 1,

i 1

где m – мощность кодового алфавита; M w w X * – мощность множе-

ства кодовых слов; li – длина кодового слова wi , wi X * , i 1, M .

1.5.Пропускная способность канала и избыточность кодирования информации

Пропускная способность канала передачи информации определяется пре-

дельным отношением числа N (t) последовательностей длительности t к этой длительности:

C lim log N (t) .

t t

В основополагающей работе К. Шеннона [28] установлено, что для любо-

го выходного алфавита Y с вектором длительностей tY t1,t2 ,...,tm пропускная способность канала без шума C tY вычисляется по формуле

где 0 tY – наибольший положительный корень уравнения

t1 t2 .. tm 1.

Вчастности, для tY t1 имеет место 0 t1 m, поэтому (1.13) принимает вид

рования определена равенством (1.12), пропускная способность канала – ра-

венством (1.13).

Определение 1.5.1. Избыточность кодирования – это разность между стоимостью кодирования на букву сообщения источника и отношением энтро-

пии источника к пропускной способности канала:

Чем меньше избыточность, тем лучше и эффективнее кодирование.

2.Некоторые методы кодирования известного источника равнозначными символами

2.1. Код Хаффмана

Данный алгоритм был предложен Дэвидом Хаффманом в 1952 году. Идея состоит в том, что символам, с наибольшей вероятностью встречающимся в со-

общении, соответствуют кодовые последовательности минимальной длины.

Код Хаффмана [27, 45, 54] является оптимальным методом кодирования в слу-

чае равных длительностей букв кодового алфавита.

Пусть заданы алфавит X x1, x2 ,..., xk и закон распределения вероятно-

стей появления букв алфавита xi p xi , i 1, k . Без ограничения общности

можно считать, что

p x1 p x2 ... p xk 0.

В процессе кодирования Хаффмана в бинарный алфавит {0, 1} строится граф-дерево, висячие вершины которого соответствуют буквам входного алфа-

вита, а ребра – кодовым буквам.

На начальном этапе дерево состоит из k изолированных вершин, соответ-

ствующих буквам входного алфавита X x1, x2 ,..., xk .

На каждом шаге алфавит будем подвергать преобразованиям посредством введения новых символов и удаления имеющихся.

Шаг построения дерева. Выбираем две наименее вероятные буквы, уда-

ляем их из алфавита X и добавляем новую букву вероятность появления кото-

19

рой положим равной сумме вероятностей удаленных букв. Добавляем к дереву вершину, соответствующую новой букве, и соединяем ее ребрами с вершинами,

соответствующими буквам, удаленным из алфавита. Полученным ребрам при-

сваиваем метки, соответствующие кодовым символам, в данном случае 0 и 1.

Возвращаемся на начало шага, рассматривая уже модифицированный алфавит.

Продолжаем процедуру до тех пор, пока алфавит не будет состоять ровно из одной буквы (корневая вершина).

Построение кода Хаффмана. Рассмотрим цепь ei1 ei2 ...eini , соединяю-

щую корневую вершину и лист, соответствующий букве xi X . Каждому реб-

ру ei j в данной цепи соответствует метка ei j , равная 0 или 1.

Кодом Хаффмана для буквы xi X является слово

Замечание. Выше описан метод кодирования в бинарный алфавит. Если же размер кодового алфавита равен, например, m, то на первом шаге кодирова-

ния следует выбрать k(mod m) букв с наименьшими вероятностями, заменяя их одной с суммарной вероятностью, а на последующих шагах по m букв.

Пример. Построим побуквенный бинарный код Хаффмена для алфавита

X x1, x2 , x3, x4 , x5 c законом распределения p (табл. 1)

Табл. 1

На первом шаге построения кода (Рис. 3) буквы x4, x5 как имеющие наименьшие вероятности удаляем из алфавита, заменяя на букву x6 с вероятно-

стью p(x6) = 0.25. Вершины кодового дерева, соответствующие буквам x4, x5,

соединяем ребрами с вершиной, соответствующей x6. Метки ребер:

20