
681_Trofimov_V.K._Teoremy_kodirovanija_neravnoznachnymi_
.pdf
3.3.Оценка стоимости кодирования известного источника неравнозначными символами
Теорема 3.3.1. Для кодирования o , p : X N Y * , где
|
w y |
j1 |
y |
|
...y |
|
, |
|
|
|||||||
o , p |
|
|
i |
|
|
|
|
j2 |
|
jn |
|
|
|
|||
имеет место неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L N, , , |
|
|
|
H ( ) E |
t** ; |
|
||||||||||
t |
|
|||||||||||||||
|
|
|||||||||||||||
|
|
Y |
|
|
|
C |
tY |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Из леммы 3.2.1. следует, что |
|
|
||||||||||||||
l |
|
w |
t** |
|
|
где t** max |
t j . |
|||||||||
p wi 0 o , p i |
|
|
, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 j m |
|
|
Логарифмируя, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
w |
|
t** |
|
|
||||
log p wi log 0 |
|
o , p |
|
i |
|
, |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
log p wi l o , p wi t ** log 0 .
Умножая на p wi , суммируя по всем словам источника и последовательно
преобразуя, получим
|
|
i |
|
|
|
|
i |
|
|
|
|
|
i |
|
|
|
o |
, p |
|
i |
|
|
|
|
|
|
0 |
|
||||||
|
|
p w log p w |
|
|
|
p w |
l |
|
|
|
w |
|
t ** log |
|
, |
|||||||||||||||||||
|
w X N |
|
|
|
|
|
|
w X N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H N |
|
|
|
|
p w |
l |
|
|
w |
|
|
t ** |
|
|
p w |
, |
|
|
||||||||||||||
|
|
|
|
|
|
o , p |
|
|
|
|||||||||||||||||||||||||
|
|
log 0 |
|
|
|
i |
|
|
|
|
i |
|
|
|
|
|
|
|
i |
|
|
|
||||||||||||
|
|
w X N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w X N |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
||
|
|
|
H N |
t ** |
|
|
|
p w |
l |
|
|
|
w |
|
|
, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
C tY |
|
|
|
|
|
|
i |
|
|
|
o , p |
|
|
i |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
w X N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H N |
t ** |
L |
N, , , |
|
. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
C |
tY |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из последнего неравенства с учетом (1.7) и (1.8) для бернуллиевских и марков-
ских источников получаем утверждение теоремы:
H N |
|
t ** |
|
L N , , , |
tY |
, |
|||
NC |
|
|
|
N |
N |
||||
t |
|
|
|
|
|||||
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|

|
NH |
|
t ** |
L N, , , |
|
|
, |
||||||||||
|
t |
||||||||||||||||
|
|
|
|
|
|
|
|||||||||||
|
NC tY |
|
N |
|
|
|
Y |
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
L N, , , |
|
|
|
H |
|
t ** |
. |
|
|||||||||
t |
|
||||||||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
Y |
|
|
C |
tY |
|
N |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема доказана.
Данная теорема означает, что избыточность предлагаемого кодирования
r N, , , |
|
L N, , , |
|
|
H |
|||
t |
t |
|||||||
|
||||||||
|
Y |
Y |
C |
tY |
|
|||
|
|
|
|
|||||
стремится к 0 с ростом длины кодируемого блока N.
4.Универсальное кодирование бернуллиевских источников буквами кодового алфавита с неравными длительностями
Приведенные выше методы кодирования строились на знании информа-
ции об источнике. А именно, эффективность данных методов достигалась за
счет того, что вероятности появления сообщений источника были известны.
В большинстве реальных ситуаций информация об источнике не дана, но
часто известен его тип. Например, рассмотрим задачу кодирования черно-
белого изображения. Очевидно, что, например, для любой страницы текста,
разбитой на точки, существует зависимость между цветом точек ''по-
соседству'', но, тем не менее, вероятность появления произвольного блока из черно-белых точек заранее не известна, и ее можно только предсказать.
Рассмотрим ситуацию, когда закон распределения вероятностей для ис-
точника информации заранее не известен. В этом случае необходим некоторый
метод универсального кодирования, т.е. кодирования, не зависящего от кон-
кретного источника и подходящего для всех источников определенного класса.
Универсальное кодирование впервые рассматривалось в работах
[2, 14, 23, 24, 50]. В [23] дано определение универсального кодирования как ко-
дирования, на котором достигается наименьшее значение избыточности на не-
42

котором множестве источников Ω, т.е. для произвольного источника вы-
полняется
|
|
|
|
|
|
|
H |
|
|
||
r N, , 0 |
, |
|
inf L N, , , |
|
|
. |
|||||
tY |
tY |
||||||||||
|
|
|
|||||||||
C tY |
|||||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
Определение 4.1. Универсальное кодирование произвольного источника сообщений – это кодирование, не зависящее от закона распределения вероятно-
стей букв алфавита источника, на котором достигается нижняя грань избыточ-
ности (1.15).
Определение 4.2. Избыточность универсального кодирования – это наибольшая разность между стоимостью наилучшего кодирования на букву сообщения источника и отношением энтропии источника к пропускной спо-
собности канала:
Yinf sup r N, , 0, tY .
Вчастности, если Ω содержит единственный источник Θ, то мы имеем дело с известным источником.
4.1.Схема кодирования множества бернуллиевских источников буквами кодового алфавита с неравными длительностями
Рассмотрим 0 – множество всех бернуллиевских источников с алфави-
том X x1, x2 ,..., xk . Пусть 0 |
– |
источник, генерирующий бесконечную |
|||||||
последовательность, которая разбивается на блоки длины N. Поскольку Θ яв- |
|||||||||
ляется |
бернуллиевским, то появление любой буквы xij X |
в сообщении |
|||||||
wi xi |
xi ...xi |
, порожденном источником Θ, не зависит от предыдущих симво- |
|||||||
1 |
2 |
N |
|
|
|
|
|
|
|
лов. Для бернуллиевского источника |
вероятность |
p wi появления блока |
|||||||
wi xi |
xi ...xi |
равна произведению вероятностей входящих в него букв: |
|||||||
1 |
2 |
N |
|
|
|
|
|
|
|
|
|
p wi p xi |
|
|
|
N |
|
. |
|
|
|
xi ...xi |
N |
p xi |
j |
(4.1) |
|||
|
|
1 |
2 |
|
j 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
Это верно для любого закона распределения вероятностей. Энтропия H
бернуллиевского источника Θ [28] определяется равенством (1.5).
43

Пусть 0 – произвольное множество бернуллиевских источников. Из основной теоремы К. Шеннона [28] следует, что избыточность универсального
кодирования R N, , |
tY , определяемая |
равенством (1.16), всегда |
неотрица- |
|
тельна. С другой стороны, с ростом |
N величины R N, , |
tY , |
0 и |
|
R N, , t1 , 0 , стремятся к нулю.
Избыточность кодирования известного источника при равных длительно-
стях кодовых символов достигает своего минимума при кодировании методом Д. Хаффмана [1, 4]. Однако этот метод не позволяет априори оценить, какой избыточности можно достигнуть при его применении.
Классический метод кодирования К. Шеннона позволил получить для из-
быточности кодирования известного бернуллиевского источника символами
алфавита с равными длительностями оценку вида
|
|
0 R N, , |
|
|
|
1 |
, |
|
. |
(4.2) |
||||||
|
|
t |
0 |
|||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
N |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р.Е. Кричевским [4] доказано, что почти для всех бернуллиевских источ- |
||||||||||||||||
ников справедливы неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
R N, , |
|
|
|
1 |
, |
|
|
, |
|
|
(4.3) |
|||
|
t |
0 |
|
|
||||||||||||
|
|
|
|
|
||||||||||||
|
N |
|
Y |
|
|
N |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где 0 . Таким образом, установлено, что код Шеннона при кодировании блоков близок к оптимальному.
Кодирование неизвестного источника впервые рассматривалось в работах
[2] и [23]. В частности, в [23] установлено, что величина R N, 0 , t1 с ростом N
стремится к нулю. Асимптотически точное значение для избыточности универ-
сального кодирования множества бернуллиевских источников символами алфа-
вита с равными длительностями получено Р. Е. Кричевским [3]. А именно, им доказано, что
R N, |
|
|
k 1 |
|
log N |
. |
|
||
, |
t |
(4.4) |
|||||||
|
|
||||||||
0 |
1 |
2 |
|
N log m |
|
||||
|
|
|
|
|
|||||
44
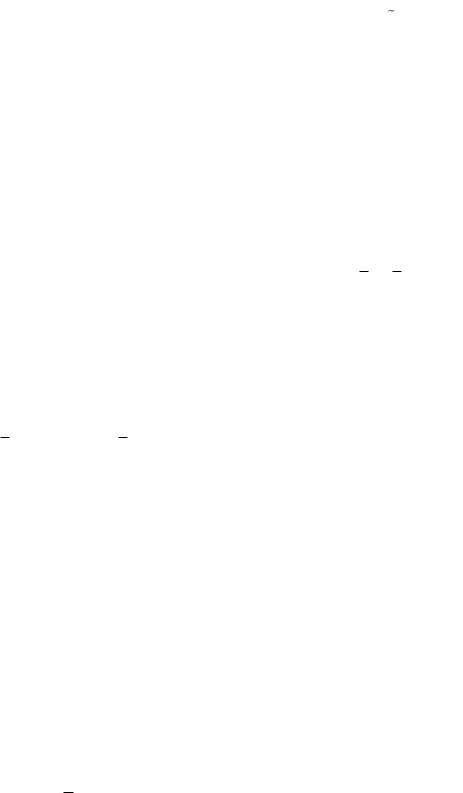
Здесь и |
далее соотношения f n g n и |
f n g n означают, что |
||||
lim |
f n |
1 и |
lim |
f n |
1 соответственно. |
|
|
|
|
||||
n g n |
|
n g n |
|
|
||
Из неравенств (4.2), (4.3) и (4.4) вытекает, что множитель log N являет-
ся «платой» за незнание источника. Так как log N растет медленнее, чем N ,
где 0 сколь угодно мало, то эту «плату» можно считать приемлемой.
Кодирование источников при неравнозначных символах кодового алфа-
вита имеет свою специфику. В частности, до настоящего времени не существу-
ет алгоритма построения оптимального кода при tY t1 , поэтому получение оценок избыточности кодирования известного бернуллиевского источника символами неравнозначного алфавита и избыточности универсального кодиро-
вания множества бернуллиевских источников символами неравнозначного ал-
фавита приобретает особое значение. При получении хороших оценок для
R N, , tY и R N, 0 , tY можно говорить если не об оптимальных кодах, то по
крайней мере о близких к оптимальным.
В работах И. Чисара [25] и И. Катоны [46] для известного источника ин-
формации были предложены коды, избыточность которых удовлетворяет нера-
венствам
0 R N, , |
|
|
|
|
, |
1. |
(4.5) |
|
t |
||||||||
|
|
|||||||
|
Y |
|
N |
|
|
|||
|
|
|
|
|
|
|||
Таким образом, при кодировании неравнозначными символами скорость
убывания избыточности совпадает со скоростью убывания избыточности при кодировании равнозначными символами.
В данной главе доказано асимптотически точное равенство для избыточ-
ности R N, 0 , tY кодирования блоков длины N, порожденных неизвестным
бернуллиевским источником, словами выходного алфавита с неравнозначными символами. Доказано асимптотическое равенство
R N, |
|
|
k 1 |
|
log N |
. |
|
||||
, |
t |
|
(4.6) |
||||||||
|
|
|
|
|
|||||||
0 |
|
Y |
|
2C tY |
|
N |
|
||||
|
|
|
|
|
|
|
|||||
|
45 |
|
|
|
|
|
|
|
|||

Сравнивая (4.5) и (4.6), видим, что «платой» за незнание источника, как и в случае равнозначности букв выходного алфавита, является множитель log N .
Итак, рассмотрим бернуллиевский источник , закон распределения ко-
торого P p (xi ) | xi X неизвестен. Поскольку для бернуллиевского ис-
точника вероятность появления буквы в сообщении не зависит от предшеству-
ющих ей букв, то вероятность p wi |
появления блока |
wi xi |
xi |
xi |
может |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
N |
быть вычислена по формуле (4.1). Зададим на множестве X N |
|
всех блоков |
||||||||||||||||||
w X N |
КТ-распределение p(w ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ni ' |
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
||||||||||||
|
p(wi ) pi |
|
2 |
|
|
i ' 1 |
|
|
|
|
|
, |
|
(4.7) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
k |
|
|
|
|
k |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 N |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
где z – гамма-функция, ni ' – число вхождений буквы xi ' в сообщение wi .
Лемма 4.1.1. (оценка плотности энтропии источника). Для бернулли-
евского источника , 0 , с алфавитом X x1, x2 ,..., xk , генерирующего
последовательности wi xi1 xi2
|
|
k 1 |
|
k 1 |
|||
|
p |
|
2 |
|
|||
log |
i |
log |
|
|
|
||
|
|
|
|||||
|
pi |
|
2e |
|
|||
xiN , верно неравенство:
|
|
|
k 1 |
|
k 1 |
|
|
||
|
1 |
|
|
2 |
|
|
|
||
|
|
log N |
|
|
|
|
|
, |
(4.8) |
|
|
|
|
|
|||||
|
2 |
|
2 |
|
|
|
|
|
|
где pi определяется равенством (2.16), а pi |
– равенством (4.7) |
Доказательство. Сравним значения |
pi и pi . Переформулировав равен- |
ство (4.1), получим |
|
k |
|
pi pni ' (xi ' ) , |
(4.9) |
i ' 1 |
|
где ni ' – число вхождений xi '
буквы xi ' X . Очевидно, что
в сообщение wi |
и p(xi ' ) – вероятность появления |
|||||
|
pi |
|
pi |
|
|
. |
|
p |
max p |
|
|||
|
|
|
||||
|
i |
|
i |
|
|
|
|
|
|
0 |
|
|
|
46

Максимальное значение функции (4.9) как функции (k-1) аргумента p (xi ) до-
|
|
|
ni ' |
|
|
|
|
|
ni ' |
|
|
|
|
|
|
|
|
|
|
|||||||||||
стигается при p(x |
) |
|
|
|
|
, i 1, k 1, |
и равно |
|||||||||||||||||||||||
k |
|
|
|
|
|
|
||||||||||||||||||||||||
|
i ' |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ni ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i ' 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max p |
|
n1n1 n2n2 |
... nknk |
. |
|
|
(4.10) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
p |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
N N |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С учетом (4.1) и (4.10) получаем равенство |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ni ' |
|
|
|
N N |
|||||||||||||
|
|
p |
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
i ' 1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
max pi |
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
n1n1 n2n2 ... nknk |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
p |
|
|
|
|
|
|
|
|
2 |
|
N |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Логарифмируя и преобразуя последнее неравенство, получим соотношение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
k |
|
|
|
log |
|
|
|
|
N N |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
log |
|
|
|
i |
|
|
log |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
n1n1 n2n2 |
... nknk |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
log |
|
|
|
|
|
log n j |
|
|
|
log N |
|
|
(4.11) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
j 1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||
Используя формулу Стирлинга в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
log z log |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
z |
|
|
|
log z |
|
|
|
z log e (z)log e , |
(4.12) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
1 |
|
1 |
(z) |
1 |
, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
2log e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
N |
k 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
k |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
pi |
|
|
k |
|
|
|
|
|
|
|
k 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
log |
|
|
|
|
log |
|
|
|
|
|
|
|
log |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
log e 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N N |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
pi |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n j |
|
|
|
N |
|
|
|
|
log e . |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С учетом ограничений в (4.12) на величину (z) неравенство принимает вид:
|
|
k 1 |
|
k 1 |
|
|
k 1 N |
|
k 1 |
k 1 |
|
|
|
||||||
|
p |
|
2 |
|
|
|
|
2 |
|
|
1 |
|
|||||||
log |
i |
log |
|
|
|
log 1 |
|
|
|
log N |
|
|
|
|
. |
||||
|
|
|
|
|
|
||||||||||||||
|
pi |
|
2 |
|
|
|
|
2N |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
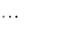
|
|
|
k 1 |
N |
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В силу того, что |
|
e 2 |
, имеем: |
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
k 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p |
|
k 1 2 |
|
k 1 2 |
|
1 |
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
log |
i |
|
log |
|
|
|
log e 2 |
log N |
|
|
|
|
. |
||||||||
|
|
|
|
|
|||||||||||||||||
|
pi |
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|||||||
Из последнего неравенства следует утверждение леммы.
Лемма доказана.
Из леммы 4.1.1. вытекает следующая лемма.
Лемма 4.1.2. (оценка информационной дивергенции распределения
источника и КТ-распределения). Для бернуллиевского источника с алфави-
том X x1, x2 ,..., xk , генерирующего последовательности wi |
xi |
xi |
xi |
, име- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
N |
|
ет место неравенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
k 1 |
|
k 1 |
|
|
|
k 1 |
k 1 |
|
|
|
||||||
|
|
|
2 |
|
|
1 |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
D p |
|
p log |
|
|
|
|
|
log N |
|
|
. |
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
2e |
|
|
2 |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||||
Доказательство.
По определению информационной дивергенции (1.9),
|
|
|
|
|
D p |
|
|
|
|
p |
k N |
|
|
pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
pi log |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
2 |
|
|
1 |
|
|
|
|
2 |
|
|
||||||||||
Тогда из леммы 4.1.1 следует, что log |
i |
log |
|
|
|
|
|
|
|
|
|
log N |
|
|
|
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
|
2e |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
||||||||
Умножая неравенство на p |
i |
и суммируя по всем w X N , получим |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
||||||
k N |
p |
k 1 |
|
|
k N |
|
|
1 k N |
|
|
|
|
|
|
|
k 1 |
|
|
k N |
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
pi log |
i |
log |
|
|
|
|
|
|
|
|
|
|
pi |
|
pi log N |
|
|
|
pi . |
|
|
|
|
||||||||||||||
pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
i 1 |
2e |
|
|
|
|
|
|
i 1 |
|
|
2 i 1 |
|
|
|
|
|
|
|
|
2 |
i 1 |
|
|
|
|
||||||||||||
k N
Так как pi 1, получаем утверждение леммы.
i 1
Лемма доказана.
48

4.2.Верхняя оценка избыточности универсального кодирования множества бернуллиевских источников
Теорема 4.2.1. Для источника с неизвестной статистикой , |
0 существу- |
||||||||||||||||||||||||
ет равномерное по входу кодирование |
0 , p |
в алфавит с неравнозначными дли- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тельностями кодовых символов, для стоимости которого имеет место оценка |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
k 1 |
|
|
|
|
k 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
log N |
|
|
|
|
t |
** |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
N , , |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
, |
(4.13) |
|
R |
|
|
, t |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 , p |
|
Y |
|
|
|
|
C tY |
N |
|
|
|
|
N |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где N – длина входного блока, C |
tY |
– пропускная способность канала, k – |
|||||||||||||||||||||||
величина, определяемая алфавитом источника, t** – константа, зависящая толь-
ко от канала.
Доказательство. Закон распределения p |
|
для источника , |
0 , не- |
||||||||||||||||||||||||
известен. Рассмотрим КТ-распределение |
|
p w |
|
, |
w X N (4.7) и кодирование |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
||
0 , p , (2.14). Тогда, из свойств разбиения Y 0;1 |
и леммы 4.1.1 следует, что |
||||||||||||||||||||||||||
|
|
|
l |
|
|
w |
|
t** |
|
|
|
|
|
|
|
|
|
t j . |
|
|
|||||||
pi |
p wi 0 |
|
|
|
0 , p |
i |
|
|
|
|
, где t |
** max |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 j m |
|
|
|
|
||
Логарифмируя данное неравенство, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
w |
t** |
|
|
|
|
|
|||||
|
log 0 pi |
|
|
|
|
|
|
|
|
|
|
0 , p |
|
|
i |
|
|
|
|
|
|
|
|
||||
|
log 0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
или после преобразования |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
log pi |
|
|
|
|
|
0 , p |
|
i |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
l |
|
|
|
|
w |
|
|
t** |
|
. |
|
|
|
|
|
||||||
|
|
log 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Умножая последнее неравенство на pi и суммируя по i , получим: |
|
||||||||||||||||||||||||||
k N |
|
|
|
|
|
|
|
k N |
|
|
|
|
|
|
w |
|
|
|
k N |
|
** |
|
|
||||
p log p log |
|
|
|
p l |
|
|
|
|
p t |
. |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
i |
i |
|
|
0 |
i |
|
0 , p |
|
|
i |
|
|
i |
|
|
|
|||||||||||
i 1 |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
||
Согласно (1.13) и (1.12) неравенство принимает вид |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k N |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
tY L |
|
0 |
, p |
t** pi log pi . |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49
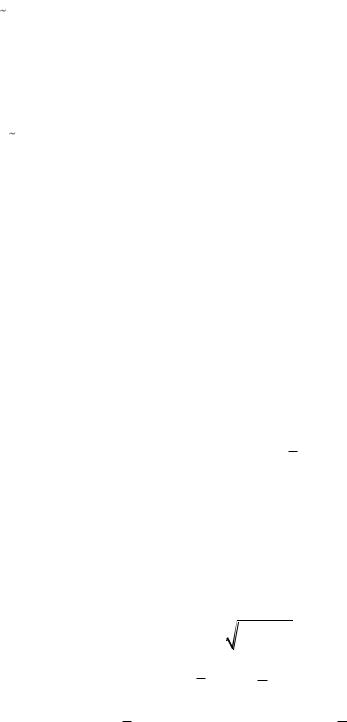
Преобразуя правую часть и используя оценку плотности энтропии (лемма
4.1.1), получаем:
|
|
|
|
|
|
|
|
|
|
|
k |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
** |
pi |
|
|
|
|
|
|
|
|
k 1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
k 1 |
|
2 |
|
||||||||||||
C tY L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||
0 |
|
|
t |
|
log pi log |
|
|
|
|
|
|
|
|
|
|
|
|
log |
N |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
, p |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
2e |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом (1.6) последнее неравенство равносильно неравенству |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
k 1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
** |
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
N |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
C tY L |
|
, p t |
|
log |
|
|
|
|
|
|
|
log N |
|
|
|
|
|
|
|
H |
|
. |
|||||||||||||||||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
2e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k log |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2e |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и учитывая равенство (1.2), получаем утверждение теоремы.
Теорема доказана.
4.3.Нижняя оценка избыточности универсального кодирования множества бернуллиевских источников
Пусть, как обычно, величина r N, , , tY , определяемая равенством
(1.15), является избыточностью кодирования . Обозначим через f рас-
пределение вероятностей, заданное на 0 , определяемое равенством
|
k |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
f |
2 |
|
|
|||
|
|
k |
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|||
1 |
. |
(4.14) |
||
|
|
|||
k |
||||
|
|
|||
|
p xi |
|
|
|
i 1 |
|
|
||
Определение 4.3.1. Величину R N, , tY , определяемую равенством
|
|
N, , |
tY inf |
|
f ( )R N, , , |
tY d , |
|
|
|
R |
(4.15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где d dp x1 ...dp xk , |
|
– k-мерный интеграл по множеству , назовем |
||||||
|
|
|
|
|
|
|
|
|
средней избыточностью универсального кодирования множества источников
.
50
