
567_Kozljaev_JU._D._SAbornik_zadach_i_uprazhnenij_po_kursu_EHlektropitanie_
.pdf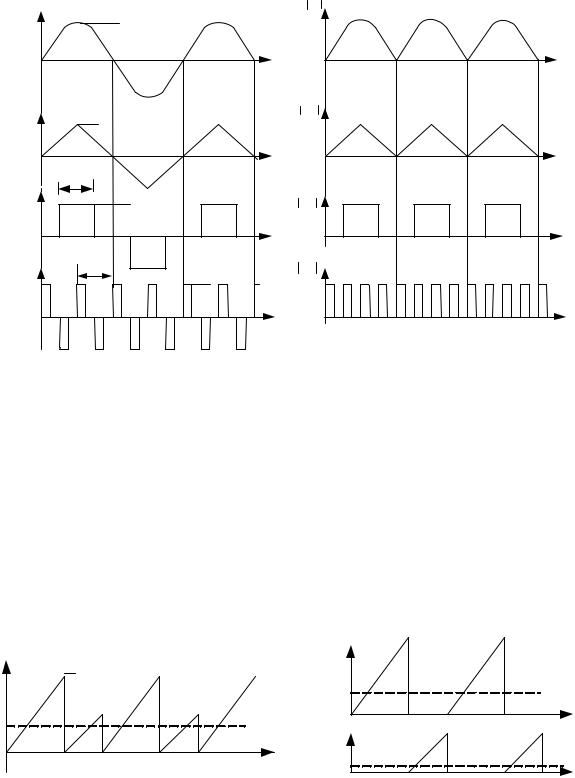
s |
Es |
|
s |
|
|
|
|
|
|
|
Ts |
t |
Ts |
t |
|
|
|
|
|
h1 |
Eh1 |
|
h2 |
|
|
|
|
|
|
|
|
t |
|
t |
|
Ти |
|
|
|
|
|
|
|
|
h2 |
Eh2 |
|
h2 |
|
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|
h3 |
Th3 |
|
h3 |
|
Eh3 |
|
|
||
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
|
|
a) |
|
б) |
|
|
|
|
|
Рис. 1.3. Примеры сигналов s(t), h(t) (a) и их модулей (б). Кратность периодов Ts/Th3 = 6
Заметим, что квадратические ошибки определяются разницей энергии сигналов s(t) и h(t) только в случае их ортогональности.
2. Примеры задач и пояснения к их решению
П.2.1. Вычислить среднее значение So пилообразного сигнала, показанно-
го на рис. П.2.1 а при А1 = 100 В, D1 = T1/T = 0.6, А2 = 60 В.
s |
|
s1 |
|
|
|
A1 |
|
So1 |
|
|
|
A2 |
|
t |
So |
|
|
|
|
s2 |
T1 T |
t |
So2 |
|
||
a) |
|
б) |
|
|
Рис. П.2.1
Решение. Представим s(t) суммой двух сигналов s1(t) и s2(t). На основании уравнения (1.1) и пояснений к нему находим: So1 = 0.5A1T1/T = 0.5A1D1 = 30 B, So2 = 0.5A2(T ‒ T1)/T = 0.5A2(1 ‒ D1) = 12 B. Суммируя полученные решения, находим: So = So1 + So2 = 42 B.
11

П.2.2. На основании графического анализа определить ожидаемую (при- |
||||
ближенную) величину среднего значения сигнала s(t) = |
Asin( t) |
(рис. П.2.2). |
||
Вычислить точное значение So. |
|
|
|
|
s |
|
|
|
|
A |
|
|
|
|
|
|
So |
|
|
0 |
|
|
t |
|
|
|
|||
|
Рис. П.2.2 |
|
|
|
Решение. А. Из графика функции следует очевидное соотношение:
So > 0.5A (для треугольного сигнала с высотой А, значение So = 0.5A). Выберем уровень линии So таким образом, чтобы площади отмеченные затемнением были примерно равны.
Из построений следует приближенное соотношение So 23 А .
Б. Точное решение найдем на основании (1.1) приняв t1 = 0, T = / :
|
|
/ |
1 |
|
|
2 |
|
|
So = |
Аsin( t)dt |
A[ cos( t)]tt 0 |
/ |
A . |
||||
|
|
|
||||||
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
П.2.3. Определить действующее значение импульсных сигналов s1(t), s2(t), показанных на рис. П.2.3. Найти действующие значения сигналов при A = 100 B и четырех значениях относительной длительности импульсов D = Ти/Т1:
D1 = 0.25, D 2 = 0.5, D 3 = 0.64, D 4 = 1.0.
s1 
|
|
|
|
A |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
Tи |
|
Т1 |
|
Т2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ти/2 |
Ти/2 |
t |
|
Рис. П.2.3
Решение. Так как квадраты сигналов s12 (t) и s 22 (t) совпадают, то при одинаковой величине D действующие значения сигналов также должны совпадать.
12

По формуле (1.4 а) находим:
|
1 |
DT1 |
|
|
|
|
|
|
DT1 |
T1 |
DT1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2T1 |
|
|
|
|||||||
|
A2 dt A |
|
|
( A2 dt |
A2 dt) A D |
|
|
|
|||||||||||
Sд1 = |
D |
, Sд2 = |
A D. |
||||||||||||||||
Т1 |
|||||||||||||||||||
|
|
|
|||||||||||||||||
|
0 |
|
|
|
|
Т 2 |
0 |
|
T |
|
|
T 2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Действующие |
значения сигналов |
при |
заданных |
значениях |
D равны: |
||||||||||||||
Sд(D1) = 50 B, Sд(D2) = 70.7 B, Sд(D3) = 80 B, Sд(D4) = 100 B.
П.2.4. Вычислить значения амплитуд первой и третьей гармоник импуль-
сного сигнала s 2 (t) (рис. П.2.3) при A = 100 B, D = 0.9.
Определить значения D, при которых обращаются в ноль гармоники с но-
мером k = 3, k = 5.
Решение. А. Общее выражение для вычисления амплитуд гармоник получим из соотношения (1.2). Переносом начала координат на интервал времени
T Т И / 2 (пунктирная линия на рис. П.2.3) представим s2(t) четной функцией. С учетом свойств четной функции находим:
2 |
TD/2 |
2 |
TD / 2 |
|
4А |
D |
|||
Umk = |
|
Acos(k t)dt |
|
A[sin(k t)] TD / 2 |
|
|
sin(k |
|
) . |
|
Tk |
k |
2 |
||||||
T |
|||||||||
|
|
TD/2 |
|
|
|
|
|
|
|
При заданных значениях А и D находим: для k = 1, Um1 = 125.8 B, для k = 3, Um3 = 37.8 B.
Б. Из общего решения следует, что гармоники обращаются в ноль при значении аргумента синуса kD / 2 = n , где n = 1,2,3… . Для k = 3 это условие выполняется при D = 2/3 = 0.667, для k = 5 при D1 = 0.4 и D2 = 0.8.
П.2.5. Вычислить амплитуду гармонического сигнала, аппроксимирующего прямоугольную функцию с высотой А (рис. П.2.5) по условию минимума квадратической ошибки.
Um |
h |
s |
A |
|
|
0 |
|
t |
Рис. П.2.5
Решение. На основании выражения (1.5 б) с учетом четности функций сигналов h(t) = Umcos( t ) и s(t) = А, ( / 2 t / 2 ) находим:
|
/ 2 |
|
2 2 |
(U m cos( t) A) 2 d t Um2 8Um A 2 A2 . |
(П.2.5) |
/ 2
13
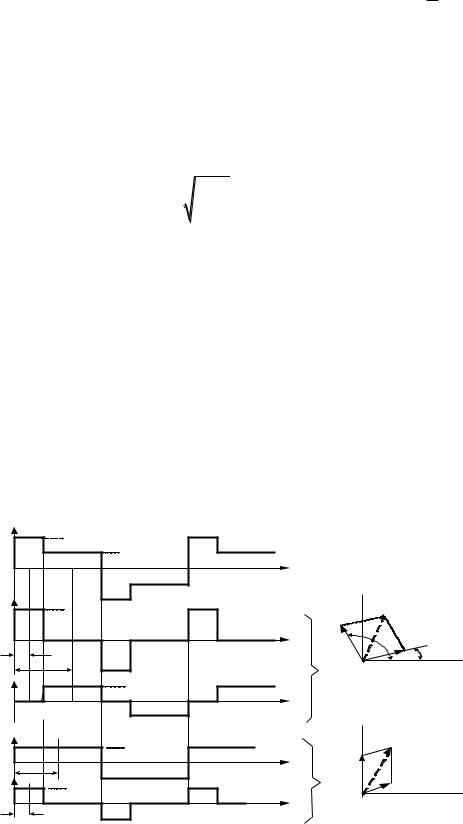
Минимум величины 2 выполняется при условии |
d 2 |
2 U m 8A 0 , откуда |
|
dU m |
|||
|
|
следует, что поставленной задаче соответствует условие Um = 4 A . Заметим,
что амплитуда первой гармоники сигнала «прямоугольный синус», полученная по формуле (1.2) дает такое же решение.
Подставляя в (П.2.5) найденное значение Um, находим минимальные ошибки аппроксимации:
22min |
2 Um2 |
|
2 |
|
1 |
|
0, 728Um2 . |
|
|
|
|
|
|||||
16 |
2 |
|||||||
|
|
|
|
|
|
2 min |
|
|
2 |
|
0.34Um . |
|
2 min |
|
|||||
2 |
||||||
|
|
|
|
|
П.2.6. На рис. П.2.6 показан сигнал s(t) ступенчатой формы. Относительная длительность «ступени» с высотой А = 2.0 имеет величину D1 = 1/3 = 0.333. Относительная длительность импульса второй ступени (с высотой 0.5А = 1.0) D2 = 2/3 = 0.667.
Определить: действующее значение сигнала и амплитуду первой гармоники сигнала.
Решение. Рассмотрим два варианта решения задачи.
Вариант 1
А. Оценка действующего значения. Представим сигнал s(t) суммой ортогональных (неперекрываемых) биэлементарных сигналов s1(t) и s2(t) (рис. П.2.6 а). А(s1) = A = 2, А(s2) = 0.5 и вычислим действующие значения элементарных сигналов (Sд1, Sд1) и их суммы (Sд):
|
s |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
0.5A |
|
|
|
|
|
|
|
|
t |
|
|
|
s1 |
|
|
|
|
|
|
|
|
|
A |
|
|
Um1(s2) |
Um1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Um1(s1) |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 |
|
|
As2=0.5A |
|
Вариант 1, сигналы |
||
|
|
|
|
||||
|
|
|
|
|
s1, s2 ортогональны |
||
0 |
|
|
|
t |
|
||
|
|
|
а) |
|
|
|
|
s3 |
|
|
Аs3=0.5A |
|
Um1(s3) |
|
|
|
|
|
|
|
|
Um1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s4 |
|
As4=0.5A |
|
|
|
Um1(s4) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
Вариант 2. |
|
|
|
|
|
|
|
||
|
|
|
б) |
|
|
||
Рис. П.2.6
14

|
|
|
|
|
1 |
1.14 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
Sд1 |
A |
D1 |
2 |
; |
Sд2 0.5A D2 |
1.0 |
|
0.82 . |
||||||||||||||
|
3 |
|||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С учетом А = 2 на основании выражения 1.4 в |
|
находим: |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
0.25 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Sд Sд21 Sд22 A |
|
|
A / |
2 1.41 . |
|||||||||||||||||
|
3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||
Б. Определим амплитуды первых гармоник составляющих сигналов используя известное расчетное выражение (табл. Приложения П.1, сигнал № 5, k = 1).
Sm1(s1) = |
4 A |
sin(k |
D1 |
) = |
4 2 |
sin( |
0.33 |
) 1.275; |
Sm1 (S 2) |
4 0.5A |
sin( |
|
D2 |
) 1.12. |
|
|
2 |
|
2 |
|
2 |
||||||||||
|
k |
|
|
|
|
|
|
|
|||||||
Так как сигналы s1 |
и s2 |
имеют взаимный фазовый сдвиг 2 1 |
/ 2 , то ре- |
||||||||||||
зультирующее значение амплитуды первой гармоники определим как
Sm1 = 
 S2m1(S1) Sm2 1(S 2) 1.684.
S2m1(S1) Sm2 1(S 2) 1.684.
Вариант 2
Представим сигнал суммой функций s3(t) и s4(t), не отвечающими условию ортогональности (рис. П.2.6, вариант 2). Высота импульса каждого из сигналов
равна значению 0.5 А, относительные длительности |
импульсов: D3 = 1.0, |
||||||||||||
D4 = 1/3 = 0.333. Фазовый сдвиг сигналов 3 |
4 |
|
|
|
(60эл.град) . |
||||||||
|
|
|
|
|
|
|
|
2 |
6 |
3 |
|
|
|
1. Определяем амплитуды первой гармоники суммируемых сигналов: |
|||||||||||||
Um1 (S 3) |
4AS 3 |
sin( |
D3 |
) |
4 |
1.27 ; Um1 (S 4) |
4AS 4 |
sin( |
D4 |
) |
4 |
0.5 0.6366 . |
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
|||||
Методом геометрического суммирования векторов, отображающих амплитуды первых гармоник сигналов, с взаимным фазовым сдвигом
φ = 6 (30эл.град.) находим результирующее значение Um1:
|
|
|
|
|
|
|
|
|
|
Um1= (U |
m(S3) |
U |
m(S 4) |
sin )2 |
(U |
m (S 4) |
cos )2 |
|
|
|
|
|
|
|
|
|
|||

 (1.27 0.6366sin( / 6))2 (0.636cos( / 6))2 1.684.
(1.27 0.6366sin( / 6))2 (0.636cos( / 6))2 1.684.
2. Действующее значение суммы сигналов. Так как сигналы не ортогональны, в решении кроме слагаемых, связанных с энергией элементарных сигналов, должна присутствовать составляющая, обусловленная «взаимной» энергией сигналов на интервале D4.
|
|
D4 |
|
|
|
|
Sд = S23 S2 |
4 2s3 ( t) s4 ( t)d t |
A32 A42 D4 2A3 A4 D4 . |
(1.6) |
|||
|
|
0 |
|
|
|
|
15
|
|
|
|
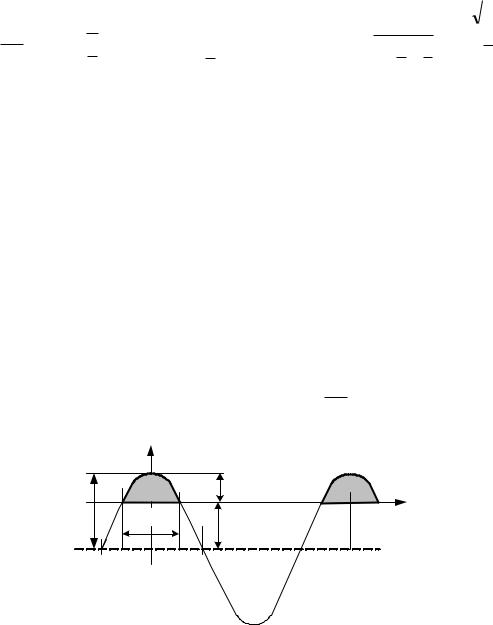
В рассматриваемом примере: D3 = 1.0, D4 =1/3 |
Sд3 A3 |
D3 0.5 A, |
|
Sд4 A4 
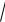 D4 0.5A
D4 0.5A
 13 , 2A1 A 4 D4 = 23 (0.5A) 2 , Sд = 0.5A
13 , 2A1 A 4 D4 = 23 (0.5A) 2 , Sд = 0.5A 
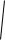 1 23 13 A /
1 23 13 A / 
 2 .
2 .
Таким образом, оба подхода дают одинаковые решения, однако трудозатраты первого варианта решения существенно ниже.
П.2.7. Исследуемый сигнал s(t) = Sm(cos t ‒ cos ) образуется методом «отсечения» от косинусоидальной функции sc(t) = Smcos( t) составляющей сигнала Е = Smcos (рис. П.2.7, сигнал s(t) обозначен затемнением). При заданных значениях Sm и угла отсечки или полного угла отсечения
Определить:
˗среднее значение (So) сигнала;
˗амплитуду отсеченного сигнала (А);
˗амплитуду первой гармоники (Um1);
˗действующее значение сигнала (S ) ‒ показатели качества: коэффициент формы (Кф), коэффициент амплитуды (Ка), при условии:
Sm = 310 B, E = 268.5 B, угол отсечки arccos( SmE ) 30эл.г рад или /6 рад.
|
s |
|
|
|
|
|
|
|
A |
|
|
Sm |
0 |
|
E=Smcos |
|
t |
|
|||||
|
|
|
|
||
|
|
|
|
|
|
Рис. П.2.7
Решение:
1. Среднее значение сигнала:
|
1 |
|
Sm |
|
310 |
|
|
|
So = |
|
Sm (cos t cos )d t |
|
(sin cos ) |
|
(0.5 |
|
0.866) 4.62 B. |
2 |
|
|
6 |
|||||
|
|
|
|
|
|
|
|
|
2.Амплитуда «отсеченного» сигнала:
А= Sm[cos(0) ‒ cos ] = Sm ‒ E=310 ‒ 268.5 = 41.5 B.
16

3. Амплитуда первой гармоники сигнала:
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
Um1= |
|
Sm (cos t cos )cos td t |
Sm (cos2 t cos cos t)d t |
|||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Sm |
|
|
|
|
|
|
|
|
|
|
|
|
310 |
|
|
|
|
|
|
|
||||
|
[0.5(1 cos 2 t) cos cos t]d t |
|
( 0.5sin 2 2sin cos ) |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
310 |
(2 sin 2 ) 8.92 |
B. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4. Действующее значение сигнала: |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
S |
|
|
|
Sm2 (cos t cos )2 d t |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
=Sm |
|
|
|
|
sin 2 4sin cos 2 cos |
|
|
|
= |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
=Sm{ |
1 |
( 0.25 0.866 4 0.5 0.866 2 |
0.8662 ) |
}1/ 2 |
= 12.14 В. |
||||||||||||||||||
|
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
||
5.Коэффициент амплитуды: Ка = А/Sд = 41.5/12.14 = 3.42.
6.Коэффициент формы сигнала: Кф = Sд/So = 12.14/4.6 = 2.64.
П.2.8. Сигнал s(t) образован перемножением синусоидального сигнала амплитудой А = 100 и пилообразного с единичной амплитудой (рис. П.2.8). Отношение частот исходных функций кратно четному числу М (в приведенном на рис. П.2.8 примере М = Т/Тт = 18, соответственно, число пилообразных импульсов на интервале синусоидальной полуволны N = 0.5M = 9).
Вычислить действующее значение сигнала s(t).
Как следует из рисунка сигнал s(t) может быть представлен суммой N сдвинутых по времени на интервал Тт знакопеременных треугольных сигналов sn(t) c амплитудой An. Один из составляющих сигналов с порядковым номером n = 3 показан на рисунке. Действующее значение «составляющего» сигнала (табл. приложения П.1 сигнал № 7), определяется соотношением:
Sд(n) |
= |
An |
D |
. В нашем примере |
D |
= |
Тт/0.5Т = 1/N, |
A·sin((n |
‒ 0.5)π/N), |
|
|
|
3 |
|
|
|
|
|
|
n = 1,2…N. n = 1,2…N. |
|
|
|
|
|
||||
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Sn |
An |
|
|
DT=Тт/0.5Т; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N=0.5T/TT=9 |
|
|
|
0 |
|
|
Тт |
|
|
|
|
t |
|
|
|
|
|
|
|
|
Т |
|
|
|
|
|
|
0.5Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аn=Asin((n-0.5) /N); |
|
|
|
|
|
|
|
|
|
n=3 |
|
|
|
|
|
|
|
|
|
0.5Т |
|
|
|
|
t |
|
|
(n-0.5)Тт |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. П 2.8 |
|
|
|||
17
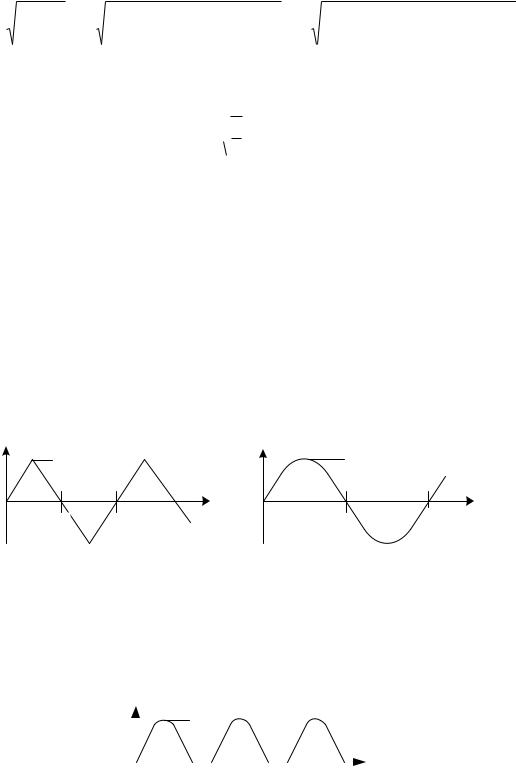
С учетом ортогональности последовательности сигналов sn(t) находим решение квадратическим суммированием их действующих значений:
N
Sд = S2(n) n 1
|
1 |
N |
1 |
N |
|
A |
sin 2 ((n 0.5) / N ) A |
[1 cos((n 0.5)2 / N )] . |
|||
|
|
||||
|
3N n 1 |
6 |
n 1 |
||
Так как значение суммы N «отсчетов» косинусоидальной функции в подкоренном выражении равно нулю, то расчетное выражение приводится к виду:
Sд =А 
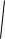 16 0.408 А.
16 0.408 А.
Для заданной по условию задачи амплитуды А = 100, Sд = 40.8.
3.Контрольные задачи
3.1.Задачи тестового уровня (А)
А.1. Сигналы пилообразной и синусоидальной формы имеют одинаковые амплитуды (Sm) и периоды повторения (Т).
Определить значения параметров:
частоту сигналов;
действующие значения сигналов (sд1, sд2);
s1
Sm
0.5T T
s2
Sm
t |
0.5T |
T |
t |
амплитуды первых гармоник (Sm1,Sm2);
показатели качества сигналов Кф и Ки.
А.2. Импульсные сигналы имеют форму синусоидальной полуволны с ча-
стотой 0 |
2 Т0 и амплитудой А. Период следования сигналов Т = NT 0 . |
||||
|
s |
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||
|
|
|
|
||
Определить среднее, действующее значения и частоту сигнала s(t) при заданных значениях А, N.
18
А.3. Сигнал имеет синусоидальную форму полуволн, сдвинутых одна относительно другой на угол N .
s
|
А |
|
|
|
t |
|
|
Определить действующее значение сигнала, амплитуду первой гармоники и коэффициент искажения сигнала при заданном значении N.
А.4. На рисунке показаны трапецеидальный сигнал h(t) с высотой импульса равной А и сигнал s(t) = Sm׀sin(ωt) ׀ с «отсечением» импульсов полуволн на уровне А. Отсеченная часть показана пунктиром.
s,h
|
|
h |
|
|
|
s |
|
Sm |
А |
|
|
|
|
|
t |
|
|
|
Определить средние значения сигналов So и Ho, величину угла ψ и ошибку первого порядка ε1 при аппроксимации одного сигнала другим.
(При вычислении So cм. пояснения к задаче П.2.7).
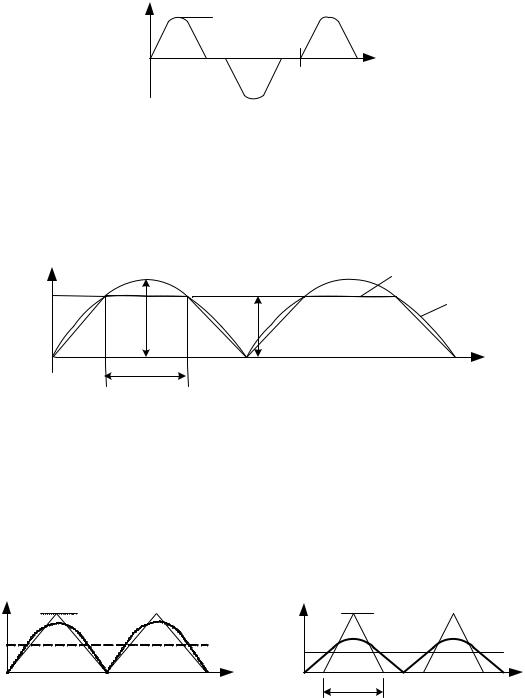
А.5. Сигнал имеет форму треугольных импульсов с периодом следования Т. Длительность основания импульсов в общем случае равна То DT , D (0...1.0) (на рисунке показаны примеры при D = 1.0 и D < 1.0).
s |
|
s |
А |
|
|
|
|
|
|
|
So |
|
T |
t |
|
2T |
|
|
|
|
To<T |
|
|
А |
|
|
|
So |
То |
Т |
t |
|
При заданных значениях А и D определить среднее значение сигналов (Sо) амплитуду аппроксимирующего синусоидального импульса и его действу-
ющее значение при условии: ошибка аппроксимации 1 0 .
19

А.6. Сигнал прямоугольной формы имеет высоту А = 100 с варьируемой величиной относительной длительности импульсов D = Ти/Т.
s
А
t
Tи T
Построить зависимости среднего и действующего значений сигнала в функции от величины D (0...1.0) . При каком значении D, среднее значение сигнала равно So = 24. Определите соответствующую этому значению D величину первой гармоники сигнала (Sm1).
|
А.7. Сигналы s1(t) и s2(t) (рис. А.7) описываются повторяющимися с пери- |
одом π фрагментами функций: |
|
а) |
s1(t) = 0 при 0 ≤ ωt ≤ α ; s1(t) = Sm sin(ωt) при α ≤ ωt ≤ π; |
б) |
s2(t) = Smsin(ωt + α) при 0 ≤ ωt ≤ π +α. |
|
Построить зависимости среднего значения сигналов So(α) при вариации |
величины α от 0 до π, при указанном в задании значения амплитуды сигнала (Sm). Определите величины α для получения указанного в задании значения
So.
s1 s2
0 |
|
|
|
t |
0 |
|
|
t |
|
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Рис. А.7
А.8. В импульсном сигнале с высотой полуволны А изменяют относительную длительность импульсов D = Ти/0.5Т от 0 до 1.0.
s
А
T
Tи |
t |
|
Определить:
1. Зависимости действующего значения сигнала и амплитуды первой гармоники от величины D. Построить в одном масштабе временные диаграммы
20
