Е.И. Иохвидов формулы обращения и некоторые их приложения

Рассматриваются линейные операторы, действующие в пространстве Крейна. Устанавливаются новые формулы, связывающие линейный оператор и его преобразование Потапова-Гинзбурга. Выводятся важные следствия этих формул

1. Рассматриваются линейные операторы в пространстве Крейна [1]. Эти операторы не предполагаются ограниченными и могут быть определены на произвольном (ненулевом) линеале этого пространства.

В этом разделе устанавливаются новые формулы, связывающие линейный оператор из класса и его преобразование Потапова-Гинзбурга, т.е. оператор

.

Теорема 1. Пусть , следовательно, существует оператор .

Тогда:

1. Оба оператора

и

являются обратимыми.

2. Имеют место формулы:

,

.

3. Следовательно, имеют место и две формулы обращения:

,

.

Доказательство. Напомним, что условие означает, по определению, обратимость оператора , т.е. условие

.

Известно также, что преобразование Потапова-Гинзбурга не выводит из класса , т.е.

.

Таким образом, оператор также является обратимым.

Перейдем к доказательству части 2) теоремы. Пусть – произвольный вектор линеала . Рассмотрим вектор

, (1)

очевидно, что

(2)

в силу общей формулы

.

Рассмотрим далее вектор вида

. (3)

Отметим, что из формулы (1) вытекает, что

(4)

(формулы (1) и (4) описывают действие преобразования Потапова-Гинзбурга).

Подставим теперь выражения (1) и (4) в формулу (3):

,

или, окончательно,

. (5)

Подставив в левую часть формулы (5) выражения (3) и (1), будем иметь:

,

. (6)

В силу произвольности вектора , эта формула означает, что

. (7)

Совершенно аналогично может быть получена формула

. (8)

Наконец, из формулы (7) вытекает

, (9)

а выражение (8) влечет за собой формулу

. (10)

Теорема доказана.

Теорема 2. Пусть , следовательно, существует оператор .

Тогда имеет место формула:

. (11)

Доказательство.

Заметим прежде всего, что операторы, стоящие в левой и правой частях формулы (11), определены на одном и том же линеале

. (12)

Пусть далее – произвольный вектор линеала , тогда

, (13)

где , при этом

. (14)

Вычислим вектор :

,

или окончательно

. (15)

Так как был произвольным вектором линеала , то из формулы (15) вытекает операторное равенство (11).

Теорема доказана.

2. В настоящем разделе выводятся некоторые важные следствия формул, установленных в теоремах 1 и 2. Всюду ниже в этом разделе предполагаем, что – произвольный оператор, принадлежащий классу , а 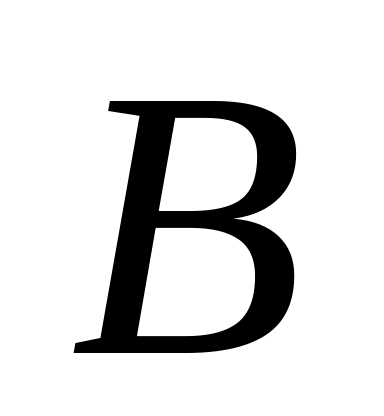– его преобразование Потапова-Гинзбурга, т.е.

.

Теорема 3. (Критерий ограниченности оператора ).

Оператор ограничен тогда и только тогда, когда оператор непрерывно обратим.

Доказательство. Утверждение непосредственно вытекает из формулы

(16)

теоремы 1, а также из ограниченности оператора .

Теорема 4. (Критерий ограниченности оператора ).

Оператор ограничен тогда и только тогда, когда ограничен оператор .

Доказательство. Это утверждение непосредственно вытекает из формулы

(17)

теоремы 2, а также из ограниченности оператора .

Далее, применяя к обеим частям формулы (16) оператор , а также , получаем:

Следствие 1. Справедливы следующие формулы:

(18)

и

. (19)

Аналогичным образом, с помощью формулы (17) можно получить:

Следствие 2. Имеют место следующие формулы:

(20)

и

. (21)

3. Хорошо известно, какую важную роль играет в теории линейных операторов в пространствах с индефинитной метрикой следующее свойство:

« Оператор ограничен тогда и только тогда, когда ограничен оператор »

Оказывается, что всякий оператор порождает другой оператор, который этим свойством обладает.

Более точно:

Теорема 5. Оператор ограничен тогда и только тогда, когда ограничен оператор

.

Доказательство. Если ограничен оператор , то в силу формулы (19), ограничен и оператор . Но тогда, в силу теоремы 3, будет ограничен оператор . Теорема доказана.

Аналогичным свойством (с заменой на ) обладает оператор а именно:

Теорема 6. Оператор ограничен в том и только том случае, когда ограничен оператор

.

Доказательство. Эту теорему, как и предыдущую, нужно доказать только «в одну сторону», поскольку операторы и являются ограниченными.

В силу формулы (20), ограниченность оператора влечет за собой ограниченность оператора . Отсюда, в силу теоремы, вытекает, что оператор будет ограниченным. Теорема доказана.

4. В заключение отметим, что доказанные выше формулы обращения, т.е. формулы

,

,

были анонсированы в докладе [2].

Литература

1. Азизов Т.Я. Основы теории линейных операторов в пространствах с индефинитной метрикой / Т.Я. Азизов, И.С. Иохвидов. – М.: Наука, 1986. – 352 с.

2. Иохвидов Е.И. Формулы обращения и критерии ограниченности линейных операторов в пространстве Крейна / Е.И. Иохвидов // Материалы Международной конференции «Дифференциальные уравнения и смежные вопросы» (Сборник тезисов). – Москва.: Издательство МГУ, 2007. – С. 120.

Воронежский государственный технический университет

УДК 621.979