В.И. Ряжских, а.В. Ряжских, в.А. Рябцев об одном способе дискретизации областей при решении краевых задач вариационными методами

Рассматривается решение краевой задачи о температурном поле тонкой изотропной пластины в вариационной постановке. Граничная часть области определения задачи, покрывается конечными элементами, а внутренняя часть - равномерной плоской сеткой. Рассмотрены проблемы формирования функционала энергии задачи и определения его минимума. Приведен пример решения указанной задачи и дана сравнительная оценка точности решения

Рассматривается вариационная формулировка краевой задачи о стационарной температурном поле тонкой плоской изотропной пластины при отсутствии теплоотдачи на внешнем контуре и поверхностях пластины. Для решения задачи предложен метод дискретизации пластины, использующий и метод конечных элементов (МКЭ) и метод конечных разностей (МКР), далее для краткости называемый гибридным методом. Рассмотрены возникающие при этом проблемы.

Уравнение стационарной теплопроводности пластины в системе координат , имеет вид

, (1)

где - абсолютная температура; - оператор Лапласа; ; .

П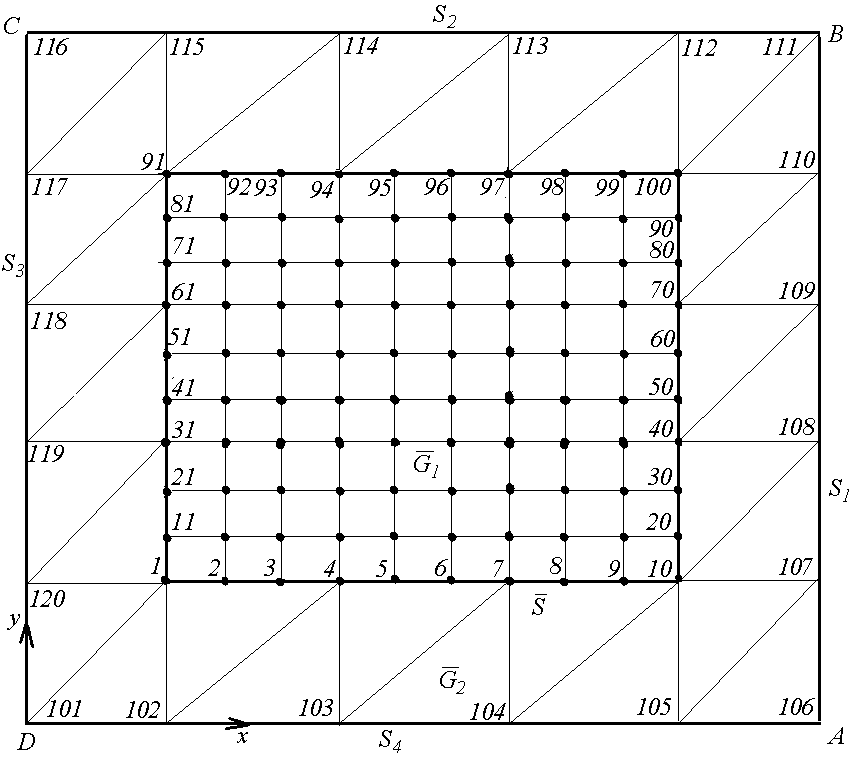 усть - область, занятая срединной плоскостью пластины в системе (рисунок), -открытое множество, а - граница . Пусть на задана температура, а на частях - теплообмен отсутствует и выполняется условие Неймана

, (2)

где - нормаль к . Если - элемент границы ; - направляющие косинусы внешней нормали к границе пластины, то энергетическая норма

, (3)

где ; ;

; .

Пусть - гильбертово пространство и не равна тождественно нулю всюду в и удовлетворяет указанным граничным условиям. Оператор является положительным в . Существование единственного решения для задачи Дирихле для оператора при смешанных краевых условиях, к которым относятся и условия Неймана.. Если функция удовлетворяет уравнению и граничным условиям, то она минимизирует функционал . Можно доказать, что смешанные граничные условия для функционала является естественным, то есть для функции , минимизирующей , эти условия удовлетворяется автоматически. Поэтому при минимизации можно использовать функции , не удовлетворяющие (2), что значительно упрощает алгоритм вычислений.

Для минимизации функционалов можно использовать дискретизацию области . В сложившейся практике для этого чаще всего используется метод конечных элементов или метод конечных разностей.

В обоих случаях существенно упрощается процесс решения задачи за счет автоматического удовлетворения естественных граничных условий. При использовании неодинаковых КЭ основной проблемой является ограниченность памяти ЭВМ, необходимой для размещения матриц КЭ, информации о координатах их узлов и матрицы связи локальных номеров узлов КЭ с их глобальными номерами и другой информации.

При использовании МКР и простой структуре области информация о сетке вполне определяется ее шагами вдоль осей координат, шаблоном, отражающим структуру формул конечно- разностных производных, перечнем номеров граничных узлов и их типов. Существенные проблемы при использовании МКР и решении систем конечно-разностных уравнений задачи возникают при формулировке смешанных граничных условий типа, в частности (2). Однако еще большие проблемы возникают при решении краевых задач для областей сложной формы или с криволинейными границами. Использование внешних узлов сетки для или внутренних узлов сетки и нецентральных разностных формул снижает и точность аппроксимации уравнения и граничных условий, и точность решения.

В работе предлагается метод решения краевых задач (1)-(2), использующий достоинства МКЭ и МКР и минимизирующий их недостатки. Метод заключается в разделении области на область простой формы, в которой краевая задача аппроксимируется МКР, и область , в которой используются конечные элементы. Очевидно, что должна включать границу области . На границе между и , являющейся внутренней для , можно не ставить никаких граничных условий, поскольку вклад в энергию системы равен нулю.

При решении задач для многосвязных областей можно использовать нескольких областей указанных типов и несколько границ типа . При таком подходе не требуется большого количества КЭ, что значительно экономит память ЭВМ. Недостатки метода - совершенно различные описания выражений функционалов типа в областях и и невозможность использования стандартных пакетов программ для ЭВМ.

Для иллюстрации гибридного метода используется задача теплопроводности квадратной пластины при заданной температуре на сторонах и (рис. 1) и условиях Неймана для сторон и . Поскольку на , , а на , , условия Неймана на границах и выполняются. Выполнение условий на и не вызывает проблем. Можно показать [3], что интегралы по и имеют постоянные значение и для определения вместо (3) можно использовать функционал

.

Для проведения вычислений производится дискретизация области МКЭ. Используется простейший треугольный элемент с узлами в вершинах (рис. 1) [1].

Пусть -температура в узлах КЭ с локальными номерами 1,2,3, соответствующими глобальным номерам узлов , а -матрица-столбец. Температура в точке с координатами и представляется в виде линейной по и функции

,

где - функция формы КЭ [2].

Пусть - номер КЭ, -количества КЭ, а - количество узлов КЭ и сетки в . Пусть - матрица- столбец узловых температур для . При замене системой КЭ заменяется функционалом

,

Вектор градиент функционала в точке

.

Область заменяется системой регулярно расположенных узлов с шагами и , а производные от температуры во внутренних узлах – центральными конечно – разностными формулами

, ,

где - номер узла сетки; -число узлов сетки в горизонтальном слое узлов.

Для аппроксимации производных от по х в точках границы использованы нецентральные разностные формулы типа

,

и аналогичные выражения для производных по .

С учетом разностных выражений для и получается , где - симметричная матрица, системы разностных уравнений, в которой неизвестными считаются величины температуры во всех узлах, покрывающих , в том числе и входящих в КЭ.

Вектор градиент функционала в точке

.

Пусть -матрица типа и для всей области . Тогда симметричная матрица, , а вектор градиент функционала в точке

.

Поскольку вторая вариация по положительна, выпукл по и, следовательно, имеет локальный минимум в . При минимизации по градиентными методами [3] требуется многократно вычислять и его градиент . При этом можно не формировать матрицу явно, поскольку вклады КЭ и узлов сетки в можно определить на основании полученных выражений. Это существенно уменьшает объем оперативной памяти ЭВМ и позволяет решать задачи с количеством КЭ и узлов порядка сотен даже на ПЭМ.

В качестве примера рассматривается задача для квадратной пластины см. Использовалось всего 32 КЭ и 120 узлов,. Приняты следующие граничные условия для . На границе - , на границе - . На отрезках - и - заданы условия отсутствия теплопередачи (условия Неймана). Точное решение для указанной задачи имеет вид , где

Вычисления проводились по оригинальной программе на алгоритмическом языке TurboPascal 7.0. Поскольку количество узлов на сторонах КЭ различно, для стыковки решений в и и определения и компонентов градиента функционала на границе использовалась линейная интерполяция. Функционал минимизировался методом градиентного спуска с проектированием градиента на область [2]. Вектор определялся по формуле , где ; - в первом приближении заданная величина и изменяющаяся в процессе вычислений с учетом информации о величине различия направлений и . В качестве начального приближения использовался вектор , удовлетворяющий граничным условиям на , и . Величины температуры во внутренних точках и сторонах и можно задавать в разумных границах произвольно. Вычисления показали, что результат минимизации слабо (в пределах вычислительных погрешностей) зависит от выбора . Наиболее быстрая сходимость процесса оптимизации наблюдается при определении компонентов линейной интерполяцией по граничным значениям температуры. Скорость сходимости вычислений, конечно, зависит и от величин температуры на границах и от выбора . При начальном = 1 решение находится за 100-200 приближений за несколько минут в режиме диалога.

Пусть и точная температура в узле и полученная в результате решения рассмотренной задачи оптимизации. Величина достигает максимума в узле 96 и отношение в этом узле равно 6,9%. Такую невысокую точность можно объяснить довольно грубым разбиением на КЭ и высокими градиентами температуры.

Литература

1. Зенкевич О. Метод конечных элементов в технике. Перевод с английского / О. Зенкевич.– Москва: Издательство Мир, 1975.-542с.

2. Поляк Б.Т. Введение в оптимизацию/ Б.Т. Поляк.– Москва: Издательство Наука, 1983.-384 с.

3. Ряжских В.И., Ряжских А.В., Рябцев В.А. Моделирование МКЭ температурного поля тонкой пластины с отверстиями при теплоотдаче на обеих поверхностях и внешней границе. «Информатика: проблемы, методология, технологии» Материалы XVII Международной научно-методической конференции, Воронеж 9-10 февраля 2017 г. Том 2. Воронеж, Издательство «Научно исследовательские публикации» ООО «Велборн», 2017, с.378-385 http://welborn@scirep.ru

Воронежский государственный технический университет

УДК.62-83:621.313.3