
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим
в пространстве прямоугольную систему
координат
![]() .
Выделим на
координатных осях
.
Выделим на
координатных осях
![]() ,
,
![]() и
и
![]() единичные векторы (орты), обозначаемые
единичные векторы (орты), обозначаемые
![]() ,
,
![]() ,
,
![]() соответственно (см. рис. 5.12).
соответственно (см. рис. 5.12).
Выберем
произвольный вектор пространства и
совместим его начало с началом координат:
![]() .
.
Найдем
проекции вектора
на координатные оси. Проведем через
конец вектора
![]() плоскости, параллельные координатным
плоскостям. Точки пересечения этих
плоскостей с осями обозначим соответственно
через
,
плоскости, параллельные координатным
плоскостям. Точки пересечения этих
плоскостей с осями обозначим соответственно
через
,
![]() и
и
![]() .
Получим прямоугольный параллелепипед,
одной из диагоналей которого является
вектор
.
Получим прямоугольный параллелепипед,
одной из диагоналей которого является
вектор
![]() .
.
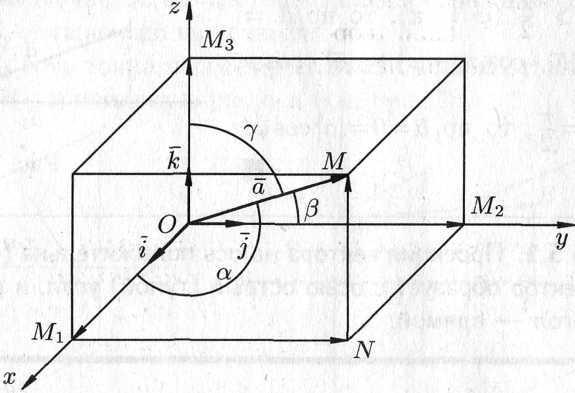
Рис. 5.12.
Тогда
![]() ,
,
![]() ,
,
![]() .
По определению суммы нескольких
векторов находим
.
По определению суммы нескольких
векторов находим
![]() .
.
А
так как
![]() ,
,
![]() ,
то
,
то
![]() .
(5.1)
.
(5.1)
Но
![]() ,
,
![]() ,
,
![]() .
(5.2)
.
(5.2)
Обозначим
проекции вектора
на оси
,
и
![]() соответственно через
соответственно через
![]() ,
,
![]() и
и
![]() ,
т. е.
,
т. е.
![]() ,
,
![]() ,
,
![]() .
Тогда из равенств (5.1) и (5.2) получаем
.
Тогда из равенств (5.1) и (5.2) получаем
![]() .
(5.3)
.
(5.3)
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.
Числа , , называются координатами вектора , т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное
равенство (5.3) часто записывают в
символическом виде:
![]() .
.
Равенство
![]() означает, что
означает, что
![]() .
.
Зная проекции вектора , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
![]() ,
т.е.
,
т.е.
![]() .
(5.4)
.
(5.4)
Отсюда
![]() ,
,
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть
углы вектора
с осями
,
и
соответственно равны
![]() ,
,
![]() ,
,
![]() .
По свойству проекции вектора на ось,
имеем
.
По свойству проекции вектора на ось,
имеем
![]() ,
, ![]() ,
, ![]() .
(5.5)
.
(5.5)
Или, что то же самое,
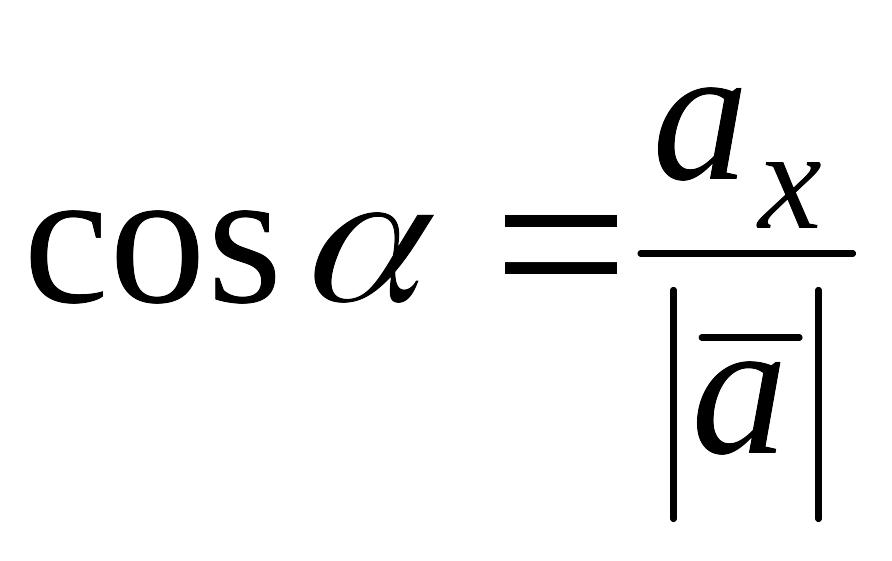 ,
,
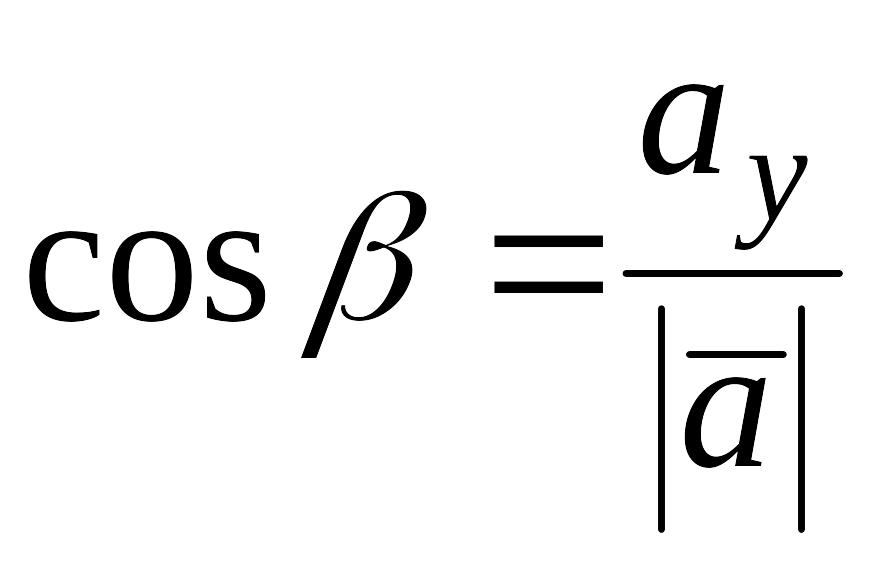 ,
,
 .
.
Числа
![]() ,
,
![]() ,
,
![]() называются направляющими
косинусами
вектора
.
называются направляющими
косинусами
вектора
.
Подставим выражения (5.5) в равенство (5.4), получаем
![]() .
.
Сократив
на
![]() ,
получим соотношение
,
получим соотношение
![]() ,
,
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко
заметить, что координатами единичного
вектора
являются числа
![]() ,
,
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() .
Итак, задав координаты вектора, всегда
можно определить его модуль и направление,
т. е. сам вектор.
.
Итак, задав координаты вектора, всегда
можно определить его модуль и направление,
т. е. сам вектор.
5.5. Действия над векторами, заданными проекциями
Пусть векторы и заданы своими проекциями на оси координат , и или, что то же самое
, .
Линейные операции над векторами.
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
1.
![]() ,
или кратко
,
или кратко
![]() .
.
То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
2.
![]() или короче
или короче
![]() .
.
То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Равенство векторов.
Из
определения вектора как направленного
отрезка, который можно передвигать в
пространстве параллельно самому себе,
следует, что два
вектора
и
равны
тогда и
только тогда, когда выполняются равенства:
![]() ,
,
![]() ,
,
![]() т. е.
т. е.
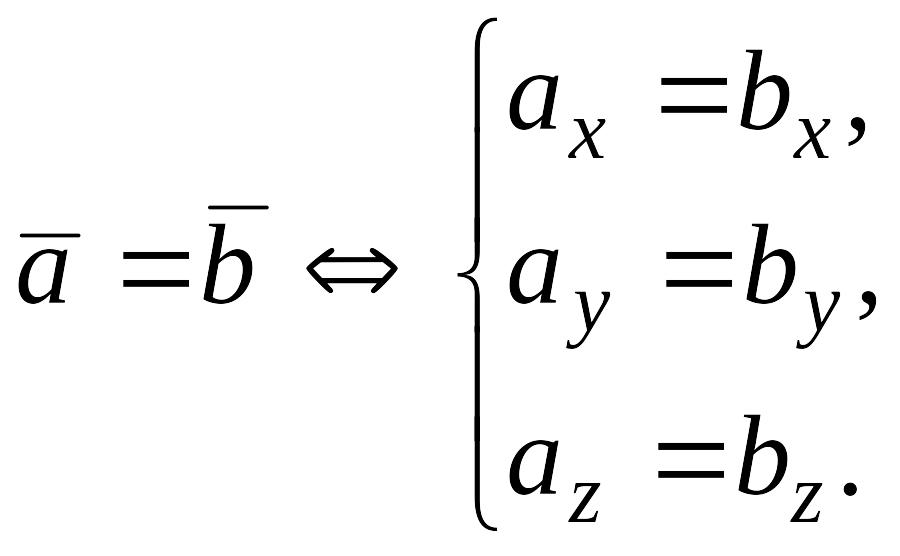
Коллинеарность векторов.
Выясним условия коллинеарности векторов и , заданных своими координатами.
Так
как
,
то можно
записать
![]() ,
где
— некоторое число. То есть
,
где
— некоторое число. То есть
![]()
![]() .
.
Отсюда
![]() ,
,
![]() ,
,
![]() .
.
т.е.
![]() ,
,
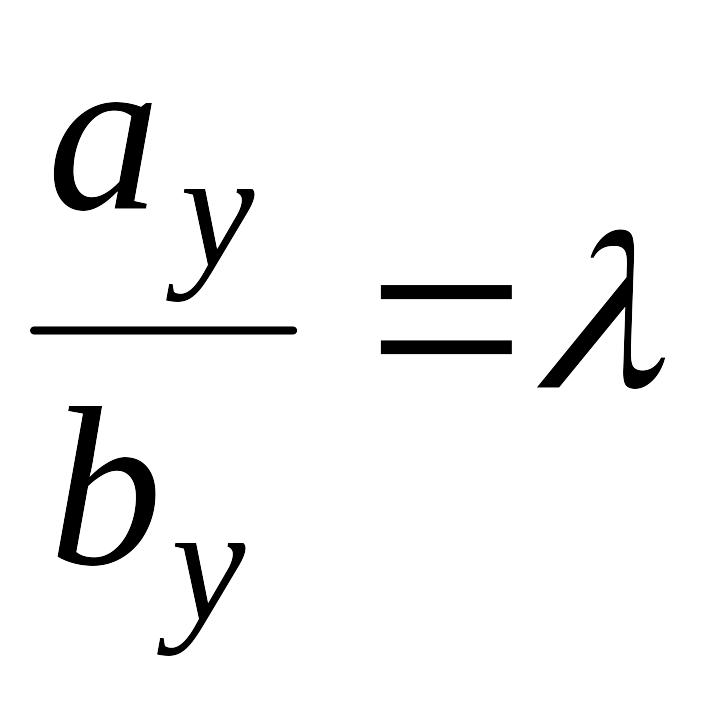 ,
,
![]() или
или
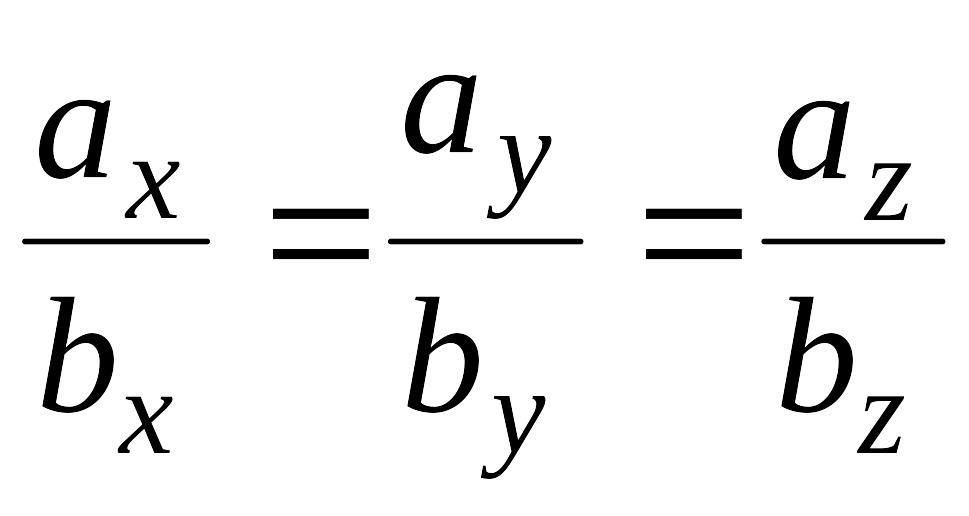 .
.
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарные.
Координаты точки.
Пусть
в пространстве задана прямоугольная
декартова система координат
.
Для любой точки
координаты вектора
называются координатами
точки
.
Вектор
называется радиус-вектором
точки
,
обозначается
![]() ,
т.е.
,
т.е.
![]() .
Следовательно,
координаты точки — это координаты ее
радиус-вектора
.
Следовательно,
координаты точки — это координаты ее
радиус-вектора
![]() или
или
![]() .
.
Координаты
точки
записываются в виде
![]() .
.
Координаты вектора.
Найдем
координаты вектора
![]() ,
если известны координаты точек
,
если известны координаты точек
![]() и
и
![]() .
Имеем (см. рис.
5.13):
.
Имеем (см. рис.
5.13):
![]()
![]() .
.
Следовательно,
координаты
вектора равны разностям соответствующих
координат его конца и начала:
![]() .
.
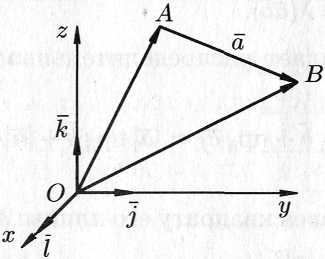
Рис. 5.13.
