
- •Часть I
- •Часть I
- •Введение
- •I. Элементы линейной алгебры
- •§1. Матрицы
- •Основные понятия
- •Действия над матрицами
- •§2. Определители
- •Основные понятия
- •2.2. Свойства определителей
- •§3. Невырожденные матрицы
- •Основные понятия
- •Обратная матрица
- •3.3. Ранг матрицы
- •§4. Системы линейных уравнений
- •Основные понятия
- •Решение систем линейных уравнений. Теорема Кронекера-Капелли
- •Решение невырожденных линейных систем. Формулы Крамера
- •Решение систем линейных уравнений методом Гаусса
- •Системы линейных однородных уравнений
- •II. Элементы векторной алгебры
- •§5. Векторы
- •5.1. Основные понятия
- •5.2. Линейные операции над векторами
- •5.3. Проекция вектора на ось
- •5.4. Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
- •5.5. Действия над векторами, заданными проекциями
- •§6. Скалярное произведение векторов и его свойства
- •6.1. Определение скалярного произведения
- •6.2. Свойства скалярного произведения
- •6.3. Выражение скалярного произведения через координаты
- •6.4. Некоторые приложения скалярного произведения
- •§ 7. Векторное произведение векторов и его свойства
- •7.1. Определение векторного произведения
- •7.2. Свойства векторного произведения
- •7.3. Выражение векторного произведения через координаты
- •7.4. Некоторые приложения векторного произведения
- •§8. Смешанное произведение векторов
- •8.1. Определение смешанного произведения, его геометрический смысл
- •8.2. Свойства смешанного произведения
- •8.3. Выражение смешанного произведения через координаты
- •8.4. Некоторые приложения смешанного произведения
- •III. Аналитическая геометрия на плоскости
- •§9. Система координат на плоскости
- •9.1. Основные понятия
- •9.2. Основные приложения метода координат на плоскости
- •9.3. Преобразование системы координат
- •§10. Линии на плоскости
- •10.1. Основные понятия
- •10.2. Уравнения прямой на плоскости
- •10.3. Прямая линия на плоскости. Основные задачи
- •§11. Линии второго порядка на плоскости
- •11.1. Основные понятия
- •11.2. Окружность
- •11.3. Эллипс
- •11.4. Гипербола
- •IV. Аналитическая геометрия в пространстве
- •§12. Уравнения поверхности и линии в пространстве
- •12.1. Основные понятия
- •12.2. Уравнения плоскости в пространстве
- •12.3. Плоскость. Основные задачи
- •12.4. Уравнения прямой в пространстве
- •12.5. Прямая линия в пространстве. Основные задачи
- •12.6. Прямая и плоскость в пространстве. Основные задачи
- •12.7. Цилиндрические поверхности
- •12.8. Поверхности вращения. Конические поверхности
- •12.9. Канонические уравнения поверхностей второго порядка
- •V. Введение в анализ
- •§13. Множества. Действительные числа
- •13.1. Основные понятия
- •13.2. Числовые множества. Множество действительных чисел
- •13.3. Числовые промежутки. Окрестность точки
- •§14. Функции
- •14.1. Понятие функции
- •14.2. Числовые функции. График функции. Способы задания функций
- •14.3. Основные характеристики функции
- •14.4. Обратная функция
- •14.5. Сложная функция
- •14.6. Основные элементарные функции и их графики
- •§15. Последовательности
- •15.1. Числовая последовательность
- •15.2. Предел числовой последовательности
- •15.3. Предельный переход в неравенствах
- •15.4. Предел монотонной ограниченной последовательности. Число . Натуральные логарифмы
- •§16. Предел функции
- •16.1. Предел функции в точке
- •16.2. Односторонние пределы
- •16.3. Предел функции при
- •16.4. Бесконечно большая функция (б.Б.Ф.)
- •§17. Бесконечно малые функции (б.М.Ф.)
- •17.1. Определения и основные теоремы
- •17.2. Связь между функцией, ее пределом и бесконечно малой функцией
- •17.3. Основные теоремы о пределах
- •17.4. Признаки существования пределов
- •17.5. Первый замечательный предел
- •17.6. Второй замечательный предел
- •§18. Эквивалентные бесконечно малые функции
- •18.1. Сравнение бесконечно малых функций
- •18.2. Эквивалентные бесконечно малые и основные теоремы о них
- •18.3. Применение эквивалентных бесконечно малых функций
- •§ 19. Непрерывность функций
- •19.1. Непрерывность функции в точке
- •19.2. Непрерывность функции в интервале и на отрезке
- •19.3. Точки разрыва функции и их классификация
- •19.4. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
- •19.5. Свойства функций, непрерывных на отрезке
- •Заключение
- •Библиографический список
- •Часть I
- •394026 Воронеж, Московский просп., 14
5.2. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.
Пусть
и
— два
произвольных вектора. Возьмем произвольную
точку
и построим вектор
![]() .
От точки
отложим вектор
.
От точки
отложим вектор
![]() .
Вектор
.
Вектор
![]() ,
соединяющий
начало первого вектора с концом второго,
называется суммой
векторов
и
:
,
соединяющий
начало первого вектора с концом второго,
называется суммой
векторов
и
:
![]() (см. рис. 5.2).
(см. рис. 5.2).
Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелограмма (см. рис. 5.3).
На рисунке 5.4 показано сложение трех векторов , и .

Рис. 5.2.
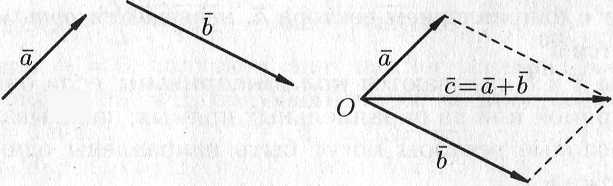
Рис. 5.3.
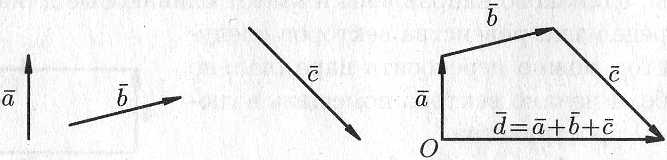
Рис. 5.4.
Под
разностью
векторов
и
понимается вектор
![]() такой, что
такой, что
![]() (см. рис. 5.5).
(см. рис. 5.5).

Рис. 5.5.
Отметим, что в параллелограмме, построенном на векторах и , одна направленная диагональ является суммой векторов и , а другая — разностью (см. рис. 5.6).
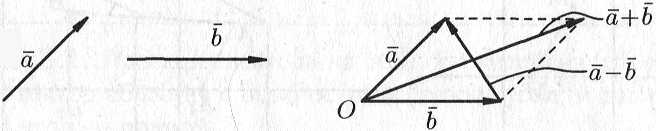
Рис. 5.6.
Можно
вычитать векторы по правилу:
![]() ,
т.е. вычитание векторов заменить
сложением вектора
с вектором, противоположным вектору
.
,
т.е. вычитание векторов заменить
сложением вектора
с вектором, противоположным вектору
.
Определение.
Произведением
вектора
на скаляр
(число)
называется
вектор
![]() (или
(или
![]() ),
который имеет длину
),
который имеет длину
![]() ,
коллинеарен вектору
,
имеет направление вектора
,
если
,
коллинеарен вектору
,
имеет направление вектора
,
если
![]() и противоположное направление, если
и противоположное направление, если
![]() .
Например, если дан вектор
=(
2,-3), то векторы
.
Например, если дан вектор
=(
2,-3), то векторы
![]() и
и
![]() будут иметь вид ( 6,-9) и (-4, 6), соответственно.
будут иметь вид ( 6,-9) и (-4, 6), соответственно.
Из определения произведения вектора на число следуют свойства этого произведения:
если
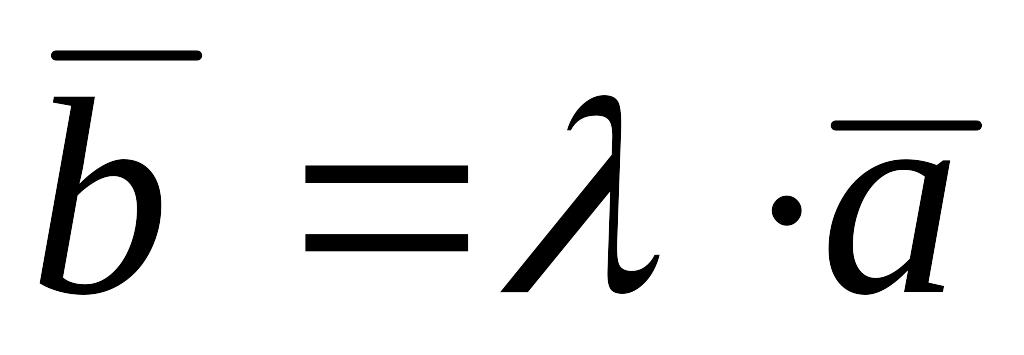 ,
то
,
то
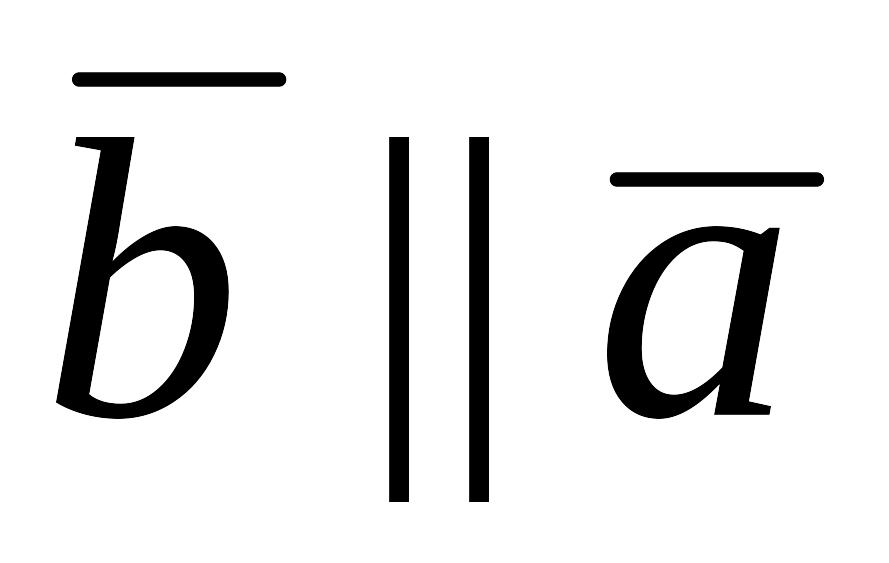 .
Наоборот, если
,
(
.
Наоборот, если
,
( ),
то, при некотором
),
то, при некотором
 верно равенство
верно равенство
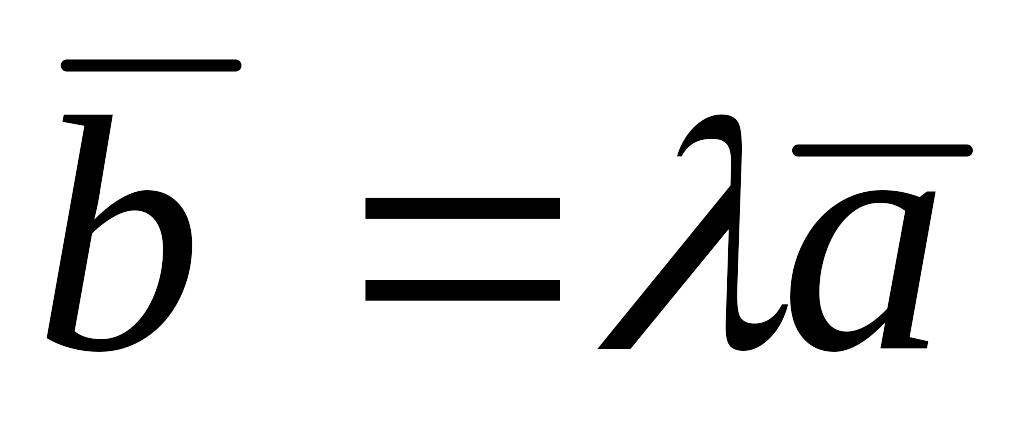 ;
;всегда
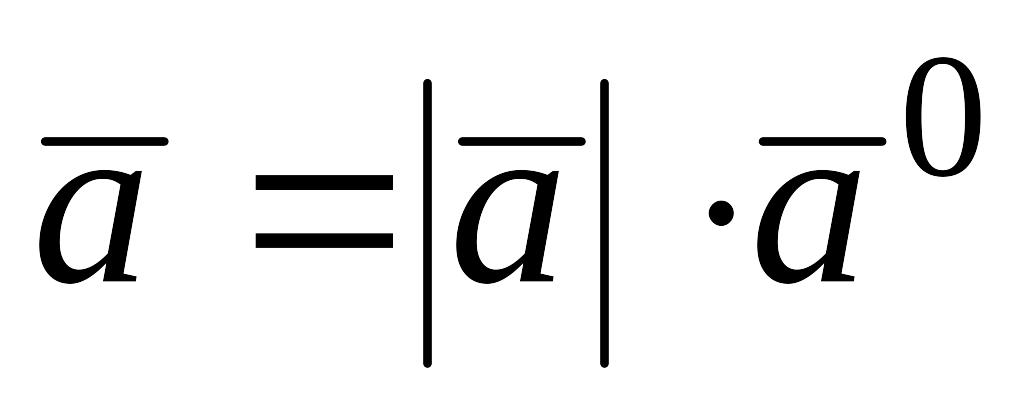 ,
т. е. каждый вектор равен произведению
его модуля на орт.
,
т. е. каждый вектор равен произведению
его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1.![]() ,
,
2.![]() ,
,
3.![]() ,
,
4.![]()
5.![]() .
.
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.
5.3. Проекция вектора на ось
Пусть
в пространстве задана ось
![]() ,
т. е. направленная прямая.
,
т. е. направленная прямая.
Определение.
Проекцией
точки
![]() на ось
называется основание
на ось
называется основание
![]() перпендикуляра
перпендикуляра
![]() ,
опущенного из точки на ось.
,
опущенного из точки на ось.
Точка есть точка пересечения оси с плоскостью, проходящей через точку перпендикулярно оси (см. рис. 5.7).
Если точка лежит на оси , то проекция точки на ось совпадает с .
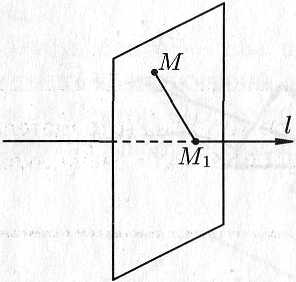
Рис. 5.7.
Пусть
— произвольный вектор (![]() ).
Обозначим через
).
Обозначим через
![]() и
и
![]() проекции на ось
соответственно начала
и конца
вектора
и рассмотрим вектор
проекции на ось
соответственно начала
и конца
вектора
и рассмотрим вектор
![]() .
.
Определение.
Проекцией
вектора
на ось
называется положительное число
![]() ,
если вектор
,
если вектор
![]() и ось
и ось
![]() одинаково направлены и отрицательное
число —
одинаково направлены и отрицательное
число —
![]() ,
если вектор
и ось
противоположно направлены (см. рис.
5.8). Если точки
и
совпадают (
,
если вектор
и ось
противоположно направлены (см. рис.
5.8). Если точки
и
совпадают (![]() ),
то проекция вектора
равна 0.
),
то проекция вектора
равна 0.
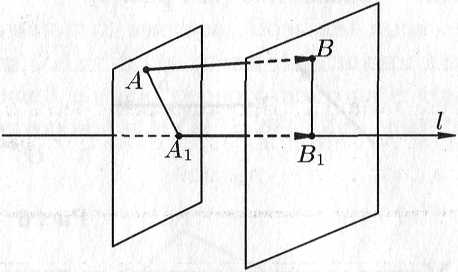
Рис. 5.8.
Проекция
вектора
на ось
обозначается так:
![]() .
Если
.
Если
![]() или
или
![]() ,
то
,
то
![]() .
.
Угол
![]() между
вектором
и осью
(или угол между двумя векторами)
изображен на рисунке 5.9. Очевидно,
между
вектором
и осью
(или угол между двумя векторами)
изображен на рисунке 5.9. Очевидно,
![]() .
.
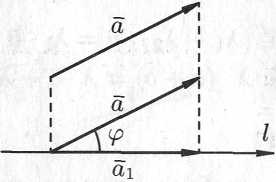
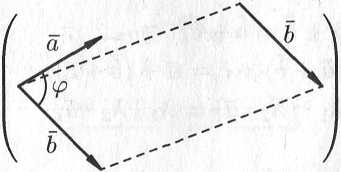
Рис. 5.9.
Рассмотрим некоторые основные свойства проекций.
Свойство
1.
Проекция
вектора
на ось
равна произведению модуля вектора
на косинус угла
между вектором и осью, т. е.
![]() (см. рис. 5.10).
(см. рис. 5.10).
Если
![]() ,
то
,
то
![]() .
.
Если
![]() (
(![]() ),
то
),
то
![]()
Если
![]() ,
то
,
то
![]() .
.
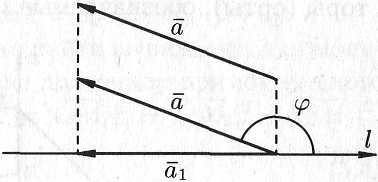
Рис. 5.10.
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол — прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.
Пусть,
например,
![]() .
Имеем
.
Имеем
![]() ,
т. е.
,
т. е.
![]() (см. рис.
5.11).
(см. рис.
5.11).
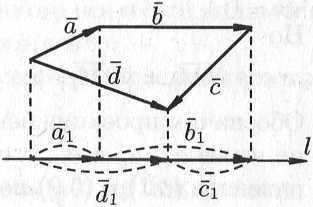
Рис. 5.11.
Свойство
3. При
умножении вектора
на число
его проекция на ось также умножается
на это число, т. е.
![]() .
.
При
имеем
![]() .
.
При
![]() :
имеем
:
имеем
![]()
![]() .
.
Свойство
справедливо, очевидно, и при
![]() .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
