4.3 Необходимые условия Лежандра

Полученные результаты преобразуем к равносильному виду, содержащему требования, положенные непосредственно на искомую функцию . Рассмотрим простейший функционал при заданных граничных условиях

. (**)

Вторая вариация такого функционала выражается формулой (33). Легко проверить, что:

если допускает при (не обязательно при всех таких x) положительные значения, то и допускает положительные значения. Если допускает при отрицательные значения, то и допускает отрицательные значения.

Д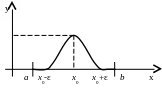 ля доказательства обозначим для краткости коэффициенты квадратичной формы под знаком интеграла (33) после подстановки в них , соответственно через и :

.

Все рассматриваемые функции и их производные считаем непрерывными (34). Поэтому, если при , то это верно и при . Предположим, что ( ). В качестве выберем ту функцию, график которой изображён на рисунке. Тогда.

.

(34)

Для вычисления этих интегралов запишем уравнения для

и

Тогда, заменив при малом ε коэффициенты их значениями в точке : , выясним приближённо значения интегралов в правой части (34).

1)

.

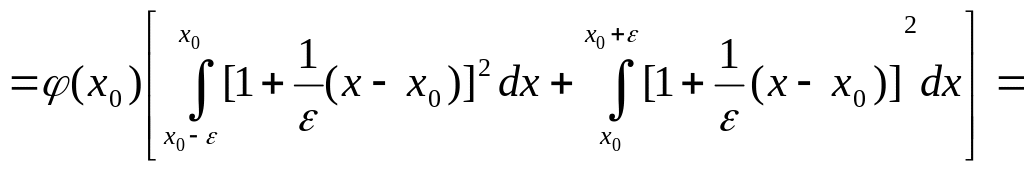
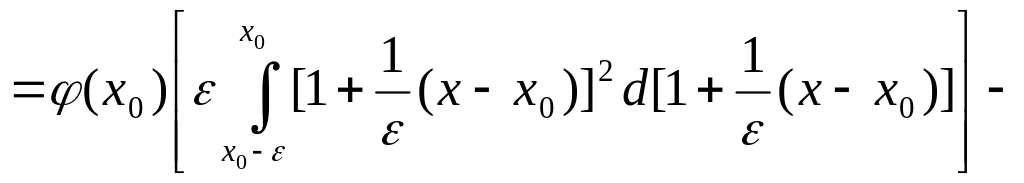
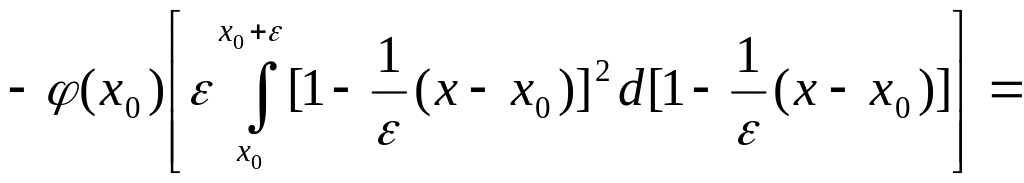
2)

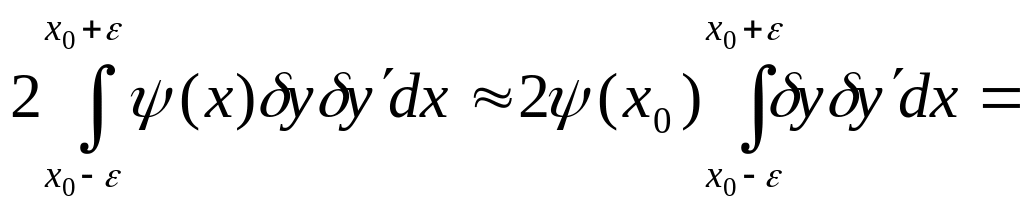
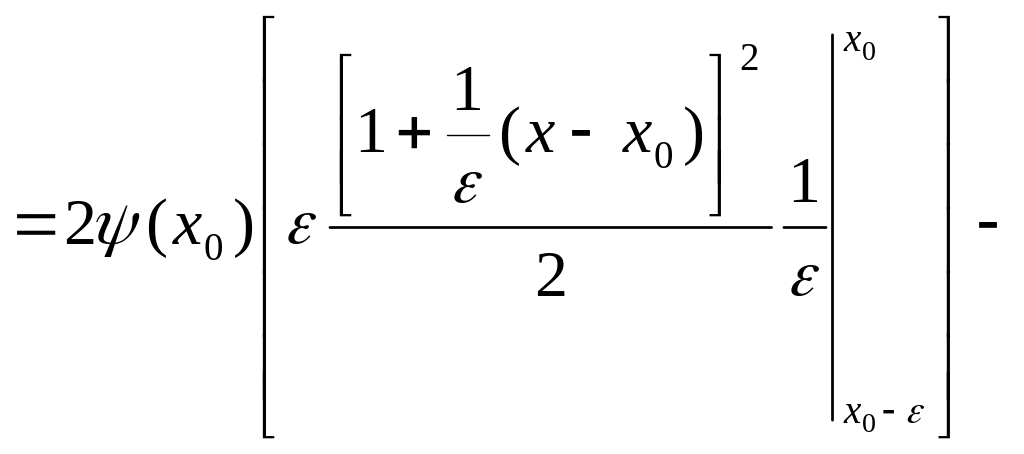
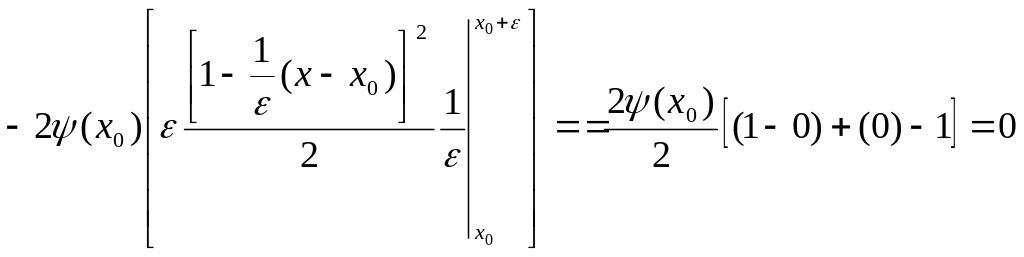
3)

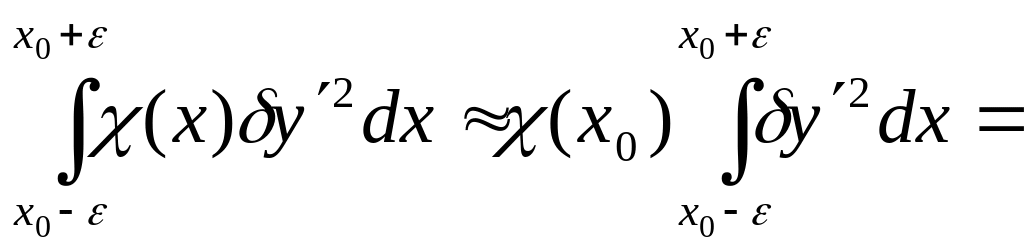
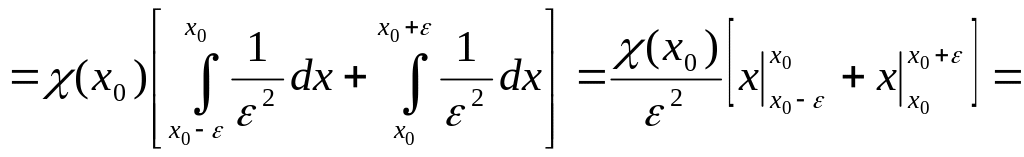
Т.о., .

Следовательно, при малом ε вся сумма в правой части положительна, что и требовалось доказать.

Сравнивая полученный результат с утверждениями п,4.2, приходим к необходимым условиям Лежандра:

если функционал (**) при некоторых граничных условиях имеет при (хотя бы слабый) минимум, то ≥0 ( ), если же максимум, то ≤0 ( ).

Одновременно получается слабое условие для минимакса^

если для экстремали функция принимает при значения обоих знаков, то при данный функционал имеет минимакс.

4.4 Поле экстремалей

Если на плоскости (x,y) через каждую точку области D проходит одна и только одна кривая семейства , то говорят, что это семейство кривых в области D образует собственное поле. Угловой коэффициент касательной p(x,y) к кривой семейства , проходящей через точку (x,y) называется наклоном поля в точке (x,y).

Н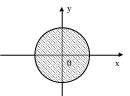 апример, внутри круга параллельные прямые y=x+c образуют поле (рис. 18.), причём наклон этого поля p(x,y)=1.

Рисунок 18.

Н апротив, семейство парабол (рис. 19.) внутри того же круга поля не образует, т.к. внутри круга параболы пере-секаются.

.

Рис. 19.

Е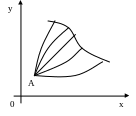 сли все кривые семейства проходят через некоторую точку , т.е. образуют пучок кривых, то они очевидно не образуют собственного поля в области D, если центр пучка принадлежит области D. Однако если кривые пучка покрывают всю область D и нигде не пересекаются в этой области, кроме центра пучка, то говорят, что семейство тоже образует поле, но не собственное, а центральное. (рисунок 20.)

Рисунок 20.

Если собственное поле образовано семейством экстремалей, некоторой вариационной задачи, то оно называется полем экстремалей.

Пусть кривая является экстремалью вариационной задачи об экстремуме простейшего функционала

,

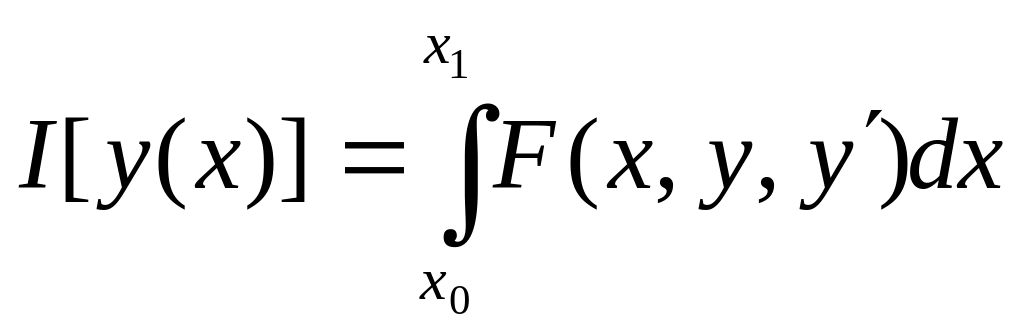п ричём граничные точки А и В(x₁,y₁) закреплены. Говорят, что экстремаль включена в поле экстремалей, если найдено семейство , образующее поле, содержащее при некотором значении С=С₀ экстремаль , причём граничные точки А и В(x₁,y₁)

Рис. 21.

закреплены. Говорят, что экстремаль включена в поле экстремалей, если найдено семейство , образующее поле, содержащее при некотором значении С=С₀ экстремаль , причём эта экстремаль не лежит на границе области D, в которой семейство образует поле (рисунок 21.).

Если пучок экстремалей с центром в точке А в окрестности экстремали, проходящей через ту же точку, образует поле, то тем самым найдено центральное

Рис. 22.

поле, включающее данную экстремаль . (рис. 22.)

Пример 17. Дан функционал , требуется

включить дугу экстремали y=0. соединяющую точки (0,0) и (a,0), где в центральное поле экстремалей.

Решение. В данном случае уравнение Эйлера имеет вид , а его решение . Из условия прохождения экстремалей через точку (0,0) получаем С₁=0 и y=С₂sinx. Кривые этого пучка на отрезке , образуют центральное поле, которое включает при С₂=0 экстремаль y=0.

4.5. Квадратичный функционал

Рассмотрим функционал (35) при граничных условиях (36) с непрерывными коэффициентами P(x) и Q(x), причём всегда будем считать P(x)>0 (a≤x≤b). Уравнение Эйлера для квадратичного функционала имеет вид

или .

Это линейное однородное дифференциальное уравнение второго порядка. Этому уравнению, а так же условиям (36) удовлетворяет частное решение y=0, придавая рассматриваемому функционалу стационарное значение. Выясним, будет ли это значение экстремальным. Ответ на этот вопрос дают следующие утверждения (без доказательства).

Рассмотрим решение уравнения (37) при начальных условиях С≠0. Если y(x) при не имеет нулей, то значение минимальное.

Квадратичный функционал общего вида

  (38)

при граничных условиях (36) приводится к виду (35) с помощью интегрирования среднего члена по частям:

.

Тогда

(39).

Запишем уравнение Эйлера для функционала (39)

(40)

Легко убедиться, что уравнение Эйлера для функционала (38) совпадает с (40). Следовательно, рассмотренные выводы о характере значения I[0] распространяется и на функционал вида (38).