Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 2044.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

4.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

2.1.8.Геометрические приложения определенного интеграла

2.1.8.1.Вычисление площадей в прямоугольных координатах

Если на отрезке [a b;] непрерывная функция f (x)≥ 0, то, как известно, площадь криволинейной трапеции, ограниченной графиком функции f (x),

осью Ox и прямыми x = a и x = b (рис. 2.1), вычисляется по формуле

S = ∫b f (x)dx .

(2.20)

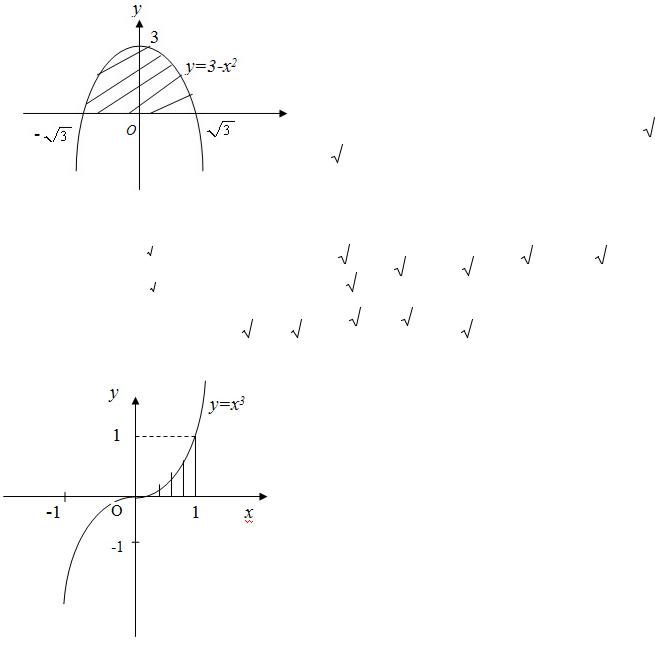
Пример 2.7. Найти площадь фигуры,

ограниченной

параболой

y = 3 − x2

осью

Ox . Изобразим фигуру в системе координат

(рис. 2.5).

Данная фигура – это криволинейная

трапеция,

ограниченная

прямыми

x = −

x =

осью

Ох

графиком

функции

y = 3 − x .

Поэтому

для

вычисления

ее

Рис. 2.5

площади применима формула (2.20):

(

(−

= 3 3 − 3(− 3)−

S = ∫

(3 − x

)dx =

3x −

−

− 3

3 3

= 3 3 + 3 3

= 4 3

(кв.ед.).

−

Пример 2.8. Найти площадь фигуры,

ограниченной

прямой

x =1,

осью

кубической параболой y = x3 .

Изобразим

фигуру

системе координат

(рис. 2.6).

Очевидно,

кубическая

парабола

пересекает

ось

при

x = 0 .

Данный

криволинейный треугольник – это фигура,

ограниченная прямыми x = 0 (Оy),

x =1,

y = 0

(Ox ) и графиком функции

y = x3 ,

поэтому для

отыскания ее площади применим формулу

(2.20):

Рис. 2.6

= ∫x

(кв.ед.).

Рассмотрим фигуру, ограниченную прямыми

x = a ,

x = b

( a <b)

графиками двух

непрерывных

на

[a b;]

функций

y = f1 (x)

y = f2 (x),

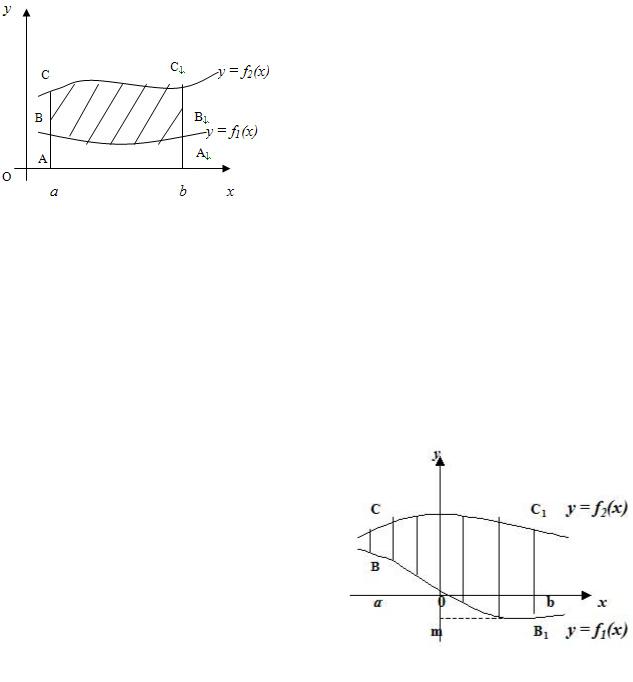
Рис. 2.7

Имеем

где f1 (x)≤ f2 (x) при x [a b;] (рис. 2.7). Найдем площадь S фигуры BCC1B1 .

Предположим вначале, что фигура расположена в верхней полуплоскости (как

на рис. 2.7), т.е. f2 (x)≥ f1 (x)≥ 0 на [a b;]. Тогда по формуле (2.20) можно найти

площади фигур ACC1 A1 и ABB1 A1 , а

разность этих площадей равна искомой площади.

SACC1A1 = ∫b	f2 (x)dx ,	SABB1A1 = ∫b	f1 (x)dx ,
a		a

откуда S = ∫b	f2 (x)dx − ∫b	f1 (x)dx или
a	a
		S = ∫b (f2 (x)− f1 (x))dx.	(2.21)
		a

Покажем, что формула (2.21) имеет место при любом расположении фигуры BCC1B относительно оси Ox . Пусть, например, эта фигура имеет вид

(рис. 2.8).	y = f1 (x)
Так как функция

непрерывна на [a b;], то она достигает

на [a b;]	наименьшего	значения,
обозначим его через m . Сдвинем
фигуру BCC1B1 вверх на m , тогда новая
фигура будет иметь ту же площадь, что
и BCC1B1 . Сдвинутая фигура будет
ограничена	прямыми x = a ,	x = b и	Рис. 2.8
графиками функций y = f1 (x)= f1 (x)+ m			Рис. 2.8
	~

и y = ~f2 (x)= f2 (x)+ m и при этом расположена в верхней полуплоскости. Ее площадь S , найденная по формуле (2.21), в которой вместо функций f1 (x) и

f2 (x) будут функции	~	~	(x), равна
	f1 (x) и	f2
b	~	~	b
S = ∫(f2 (x)− f1			(x))dx = ∫(( f2 (x)+ m) −( f1 (x)+ m))dx
a			a
или, раскрывая скобки, получаем для вычисления S формулу (2.21).
Вывод. Если фигура зажата слева и справа между прямыми x = a , x = b
( a <b), а снизу и сверху –		между графиками функций y = f1 (x) (снизу) и

y = f2 (x) (сверху), то площадь такой фигуры равна определенному интегралу по отрезку [a b;] от разности большей и меньшей функций.

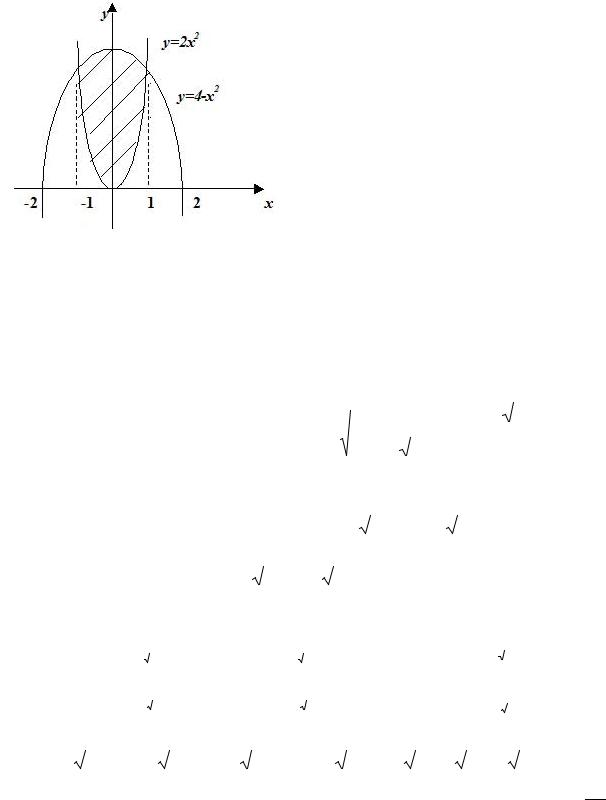
																									Пример 2.9. Найти площадь
																		фигуры,															ограниченной															параболами
																			y = 4 − x2 и y = 2x2 .
																									Изобразим													фигуру									в			плоскости
																			xOy (рис. 2.9).
																									Очевидно, фигура зажата между
																		прямыми															x = a ,						x = b ,						проходящими
																		через точки пересечения парабол, т.е. a
																		и b - это абсциссы этих точек. Чтобы
																		найти точки пересечения парабол,
																		решим систему																					их			уравнений, т.е.
			Рис. 2.9															систему
																													y = 2x2 ,

Решая, получим																													y = 4 − x2 .
Решая, получим
																									y = 2x								2											2
		y = 2x2								y = 2x2																														x = ±

																																				2								3					,
																													4
																													4
		y =		4 − x2						3x2 =					4			x = ±									3					= ±									y =			8

																																				3
																																				3								3
																																												3
																															2				8					2		8
т.е. точки пересечения имеют координаты																											−							;	3	и					;	3		. Итак, фигура
т.е. точки пересечения имеют координаты																											−							;		и					;			. Итак, фигура
																																3								3
«зажата» между прямыми x = −															2		,	x =						2				, а снизу и сверху у нее графики
«зажата» между прямыми x = −																	,	x =										, а снизу и сверху у нее графики
																3							3
функций y = x2 (снизу) и y = 4 − x2																	(сверху), поэтому по формуле (2.21)
				2															2																					2x3				2
				2															2																									2
			S		3		((4 − x				2	)− x		2	)dx						3		(4 −			2x				2								−								3
			S	= ∫			((4 − x					)− x			)dx		= ∫						(4 −			2x						)dx = 4x						−		3				=
				2															2																					3				2
				−															−																								−
				−		3													−			3
						3																3																									3
	2							2					2 2			3			2							2 3										16				32				112
= 4			− 4	−						−							−						−											=			−					=								≈ 7 (кв.ед.).


	3								3				3		3					3								3								3 9 3 9 3
	3								3				3		3					3								3								3 9 3 9 3

Пример 2.10. Найти площадь фигуры, ограниченной линиями y = 2x , y = 3x и y = 4 − x .

Изобразим фигуру в системе координат (рис. 2.10).

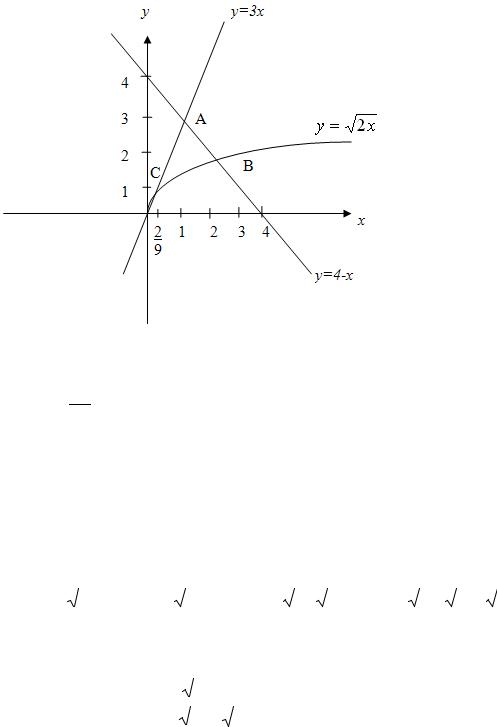
Рис. 2.10

Полученный «криволинейный треугольник» зажат слева и справа прямыми, проходящими через точки С и B параллельно Oy ; снизу – график

функции y = 2x , а сверху – ломаная из графиков двух функций. Сразу

применение формулы (2.21) невозможно, но если провести через точку A прямую, параллельную Oy , то фигура разобьется на две, к каждой из

которых применима формула (2.21). Найдем координаты точек пересечения

всех линий, т.е. точек C ,

B .

Для этого решим системы уравнений:

y = 3x,

y =

3x,

y = 3x,

y = 3x

C :

y =

2x,

= 0,

x(3 x − 2)= 0

3x =

3x − 2 x

x = 0,

y = 3x,

y = 0,

x = 0,

x =

3 x = 2,

y =

Найденные точки O(0,0),

. Теперь найдем точку A.

y = 3x,

x =1,

A :

, т.е. A(1,3). И, наконец,

y =

4 − x,

x =1,

y = 3

3x =

находим точку B :

					B :			y = 4 − x,																									y = 4 − x,																										y = 4 − x,

																			2x																																									2 x − 4 = 0.
								y =											2x										4 − x = 2x,																								x +							2 x − 4 = 0.
Решаем уравнение (														)2			+													− 4 = 0 , квадратное относительно																																																				.
Решаем уравнение (												x		)2			+					2							x	− 4 = 0 , квадратное относительно																																																	x			.
					= −										±																= −								±3											,																= −										±3							=
Получим				1,2								2								2 + 4 4																	2										2							т.е.																				2						2									,
Получим			x	1,2								2								2 + 4 4																	2										2							т.е.										x										2						2								2	,
																	2						−3															2																																					2
т.е.	x = 2,		или										= −								2									2				= −2												-							не				подходит,																		т.к.											≥ 0.
т.е.	x = 2,		или								x		= −								2									2				= −2						2						-							не				подходит,																		т.к.										x	≥ 0.
																					2																																								B(2,2).
Подставляя x = 2 в систему, получим x = 2,																																													y = 2 , т.е.																B(2,2).
	Левый «треугольник» зажат между прямыми																																																					x = 2											и					x =1,			снизу –
																																																																	9
график функции y = 2																		, а сверху – y = 3x , поэтому его площадь S1																																																		равна
график функции y = 2																x		, а сверху – y = 3x , поэтому его площадь S1																																																		равна
																																						3						1																																								3


			1																								x2										x2														3								4									2 2										2						2
			1																								x2										x2														3								4									2 2										2						2
	S1 = ∫(3x − 2x )dx																		=		3										− 2															=								1		−									−								1−														=
	S1 = ∫(3x − 2x )dx																		=		3					2					− 2													2		=					2			1		−		81							−				3				1−					9									=
			2																							2										3 2								2							2							81											3									9
			9																																									9
			9																																									9

											77								2		2										2				2								247											2			2
								=			77						−		2		2										2				2			=					247									−		2			2						(кв. ед.).
								=			54						−		3						1−							27						=					162									−			3								(кв. ед.).
											54								3													27											162												3
Правый треугольник зажат между прямыми																																																	x =1 и												x = 2, снизу –																				график
функции y = 2						, а сверху − y = 4 − x , поэтому его площадь S2 равна
функции y = 2					x	, а сверху − y = 4 − x , поэтому его площадь S2 равна
																																																																	3					2
																																																																	3
																	2																																			x		2									x2
																	2																																			x											x2
									S2 = ∫(4 − x −																						2x )dx							=				4x						−							−				2											1	=
									S2 = ∫(4 − x −																						2x )dx							=				4x						−					2		−				2			3 2									=
																	1																																				2									3 2



	= 4(2 −1)					1		(2									1)				2 2								(2 2 −1)=													5							8						2 2												2 2								1
					−	1						2			−				−		2 2																					5			−				8				+		2 2						=						2 2						−		1
					−	2									−				−					3																		2			−				3				+			3					=							3					−		6		(кв. ед.).
						2																		3																		2							3							3												3							6
Площадь S всей фигуры ABC равна
					247								2
																										2				2					1						247												1				220										110
S = S1 + S2										−								2			+					2				2				−	1			=			247								−				1		=		220								=		110					≈1,36						(кв.ед.).
S = S1 + S2			=		162					−						3					+							3						−	6			=			162								−				6		=		162								=			81				≈1,36						(кв.ед.).
					162											3												3							6						162												6				162											81
	Пусть дана фигура, «зажатая» снизу и сверху между прямыми																																																					y = c ,
y = d	(c <d ), и графиками непрерывных
на [c;d]		функций,									x = g1 (y)															и				x = g2 (y)
слева	и	справа					(т.е.											g1 (y)≤ g2 (y)																		при

y [c;d]), (рис. 2.11.)

Чтобы найти площадь этой фигуры,

нужно повернуть чертеж на 90° против

часовой стрелки. Мы увидим, что данная

Рис. 2.11

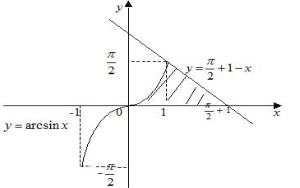
фигура аналогична фигуре на рис. 2.11, лишь поменялись ролями переменные x и y . Поэтому искомая площадь вычисляется по формуле,

аналогичной формуле (2.21), т.е.
S = ∫d (g2 (y)− g1 (y))dy .			(2.22)
c
Пример 2.11. Найти площадь фигуры, ограниченной осью Ox ,
графиком функции y = arcsin x и прямой y = π +1− x .
	2
Изобразим фигуру на плоскости xOy (рис. 2.12).
	Можно найти площадь данной
	фигуры, используя формулу (2.21),
	разбив ее на две части, а затем,
	сложив площади этих частей
		π
	1	2 π
	S = ∫arcsin xdx +	∫	+1− x dx .
	0	1 2
Рис. 2.12	Вычисление первого		интеграла не
Рис. 2.12	очень простое. Попробуем повернуть

чертеж на 90° против часовой стрелки. Видно, что это фигура такого же типа,

как на рис. 2.12, где с = 0, d =

π ,

g1 (y)= sin y , g2 (y)=

+1− y

(уравнение

π +1− x

y = arcsin x

переписали в виде

x = sin y , а уравнение y =

– в виде

x = π +1− y ). Применив формулу (2.22), получим

2 π

S = ∫

+1− y

−sin y dy =

+1 y −

+ cos y

0 2

−

π 2

+ сos

0 + cos 0)=

−(0 −

2 2

π 2

−

π 2

+ 0

−1 =

π 2

−1 ≈ 1.8 (кв. ед.).

Пусть

дана криволинейная

трапеция

(см. рис.

2.1), где

функция

y = f (x) задана параметрически

x =ϕ(t),

(t),

y =ψ

причем a =ϕ(α), b =ϕ(β). Найдем площадь этой трапеции по формуле (2.20). Так как S = ∫b f (x)dx , то заменим x =ϕ(t) в определенном интеграле и

при этом учтем,

f (x)= y =ψ

(t), dx

=ϕ

(t)dt ,

нижний

и верхний

что

′

пределы интегрирования для переменной t

будут соответственно равны α и

β . Получим формулу

′

(2.23)

= ∫ψ(t) ϕ (t)dt .

Пример 2.12. Вычислить площадь области, ограниченной эллипсом

x = a cos t,

0 ≤ t ≤ 2π .

y = bsin t,

Изобразим данную область (рис. 2.13).

Как известно, данный эллипс

симметричен

относительно

координатных

осей.

Рассмотрим

половину области, лежащую в верхней

полуплоскости. Она ограничена прямыми

x = ±a , осью Ox и эллипсом,

заданным

параметрически.

Для

вычисления

площади

половины

области

применима

формула

(2.23), в

которой ϕ(t)= a cost ,

Рис. 2.13

ψ(t)= bsin t ,

α =π

(т.к.

ϕ(π)= a cosπ = −a )

β = 0 (т.к.

ϕ(0)= a cos 0 = a ).

По формуле

(2.23)

площадь половины области

′

0 1

−cost

dt =

S1 = ∫bsin t (a cost) dt

= −ab∫sin

tdt = −ab∫

= −ab

sin 2t

= −

(−π)=

πab

t −

0 −π −

(sin 0 −sin 2π)

Искомая площадь S = 2S

= 2 πab =πab (кв. ед.).

2.1.8.2. Площадь криволинейного сектора в полярной системе координат

Рассмотрим на плоскости полярную систему координат и фигуру,

ограниченную

двумя

лучами

ϕ =α , ϕ = β

(α <β )

и линией,

уравнение

которой в полярной системе координат имеет вид

ρ = f (ϕ),

где

f (ϕ)

непрерывна при ϕ [α, β], рис. 2.14.

ϕ=β

ϕ=α

	O		1			ρ=f(ϕ)	P
						ρ=f(ϕ)
						Рис. 2.14
Назовем такую фигуру криволинейным сектором. Площадь этого
сектора можно найти по формуле				1	β
		S =		1	β	2	(2.24)
		S =		2	∫(f (ϕ)) dϕ ,		(2.24)
				2	α

вывод которой будет получен далее при изучении двойных интегралов.

Пример 2.13. Найти площадь фигуры, ограниченной полярной осью и спиралью Архимеда ρ =ϕ (ϕ [0,2π]), рис.2.15.

Рис. 2.15

Можно считать, что данная фигура – это криволинейный сектор,

ограниченный кривой ρ =ϕ

и двумя лучами ϕ = 0

и ϕ = 2π , поэтому по

формуле (2.24) получим

S =

2π

dϕ =

1 ϕ3

2π

8π

(кв. ед.).

∫

Пример 2.14. Найти площадь верхней части круга, ограниченной

окружностью x2 − 2x + y2

= 0 и прямой y = x .

Перепишем уравнение

окружности

виде

(x2 − 2x +1) + y2 =1 или

	(x −1)2 + y2		=1.		Видно,	что		центр
	окружности		в		точке (1;0),		а	радиус
	R =1.	Изобразим данную					фигуру		в
	плоскости xOy , рис. 2.16.
		Искомую площадь можно найти
	по формуле
		S = ∫b (f2 (x)− f1 (x))dx ,
		a
		f2 (x)=
Рис. 2.16	где	f2 (x)=		1−(x −1)2		(нашли			из
уравнения окружности), а	f1 (x)= x , т.е.

S = ∫1 (1−(x −1)2 − x)dx .

Найти такой интеграл непросто. Но если мы введем на плоскости полярную систему координат, полярная ось которой совпадает с Ox , то уравнения линий, ограничивающих данную фигуру, упростятся. Так как полярные и декартовы координаты точек в этих системах координат связаны равенствами x = ρ cosϕ, y = ρ sinϕ , то уравнение окружности примет вид

(ρ cosϕ)2 − 2ρ cosϕ + (ρ sinϕ)2 = 0,

или

ρ2 (cos2 ϕ +sin2 ϕ) = 2ρ cosϕ , т.е. ρ2 = 2ρ cosϕ ,

откуда либо ρ = 0 (точка 0), либо ρ = 2cosϕ . Прямая y = x имеет полярное

уравнение

ρ sinϕ = ρ cosϕ, откуда

либо

ρ = 0 (точка

0), либо tgϕ =1

ϕ =

(луч в I

четв.), либо ϕ =

5π

(луч в III четв.). Данная фигура –

это

криволинейный сектор,

ограниченный линией ρ = 2cosϕ

и лучами ϕ =

ϕ =

(ось Oy ). По формуле (2.24)

S =

dϕ =

2 1+ cos 2ϕ

dϕ

sin 2ϕ

∫(2cosϕ)

4∫

ϕ +

−

−1)=

−

≈ 0,285 (кв.ед.).

sin 2

−sin

Пример 2.15. Найти площадь фигуры, ограниченной линиями, уравнения которых в полярной системе координат имеют вид ρ =1−cosϕ и

ρ = 2(1−cosϕ) (обе линии – кардиоиды, рис. 2.17).

Очевидно,

эта

фигура

симметрична относительно оси Ox ,

поэтому

найдем площадь

половины

фигуры,

лежащей

верхней

полуплоскости

(0 ≤ϕ ≤π ),

затем

умножим на два.

Эту площадь можно найти как

разность

площадей

фигур,

ограниченных

большой и

маленькой

Рис. 2.17

кардиоидами и лучами ϕ = 0 и ϕ =π .

По формуле (2.24)

1 π

S = 2(S2

− S1 )= 2

2 ∫0

(2(1−cosϕ)) dϕ −

2 ∫0

(1−cosϕ) dϕ =

= 2 1

∫(4(1−cosϕ)2 −(1−cosϕ)2 )dϕ =3∫(1−cosϕ)2 dϕ =

2 0

+ cos2ϕ

=3∫(1 − 2cosϕ + cos

− 2sin

+ ∫

ϕ)dϕ = 3 ϕ

dϕ =

= 3 π − 2sin π + 2sin 0 +

ϕ +

sin 2ϕ

= 3π +

sin 2π −

sin 0

= 3π

π = 4,5π (кв. ед.).

π −0 +

2.1.8.3. Вычисление длины дуги плоской кривой

Пусть на

плоскости

xOy

задан

график

непрерывной

y=f(x)

функции

y = f (x). Возьмем

на

этой линии две точки A(a, f (a)) и

B(b, f (b)), где a <b (рис. 2.18).

Если функция

f (x) имеет

Рис. 2.18

непрерывную

производную

на

отрезке [a,b], то длина дуги AB может быть найдена по формуле

l = ∫b

dx,

1+(f ′(x))2

(2.25)

вывод которой получим при изучении

криволинейных интегралов.

Пример 2.16. Найти длину дуги графика

функции y = ln x от точки A(1,0) до точки B(e,1),

(рис. 2.19).

Рис. 2.19

Используем формулу (2.25).

Здесь f (x)= ln x ,

′

a =1,

b = e ,

(x)= x ,

поэтому

x2 +1

l = ∫ 1+

dx =

∫

dx = ∫

dx =

∫

dx =

x2 dx

xdx

= ∫

+ ∫

= ∫

+ ∫

x x

1 d(x2 +1)

− d

= ∫

+ ∫

∫

(x2 +1)−

(x2 +1)+

∫

1 +

воспользуемся табличными интегралами

∫x−2 dx =

2 x + C и ∫

2 = ln x + 1 + x2 + C

1 + x

+1 − ln

1 +

+1 −

2 −

− ln1

1 +

−

ln(1 +

)+ ln e + ln(1 +

e2 +1

−

+1 − ln1 +

e2 +1

≈ 2 (ед.).

2 +1

x =ϕ(t)

Если функция

y = f (x)

задана параметрически

а значения

(t)

y =ψ

параметра t , соответствующие точкам

A и B на графике, равны t1 и t2 , то

для

вычисления

длины дуги

графика по

формуле

(2.25)

сделаем

′

интеграле замену переменной x = ϕ(t),

′

ψ (t)

(по формуле

′

dx =ϕ (t)dt ,

f (x)=

ϕ (t)

дифференцирования функции, заданной параметрически).

Учитывая,

что

ϕ(t1 )= a , ϕ(t2 )= b , имеем

′

(f (x))

ϕ (t)dt .

l = ∫ 1 +

dx =∫

′(t)

Если t1 <t2 , то, учитывая, что b = ϕ(t2 )>a = ϕ(t1 ), делаем вывод, что ϕ(t)

возрастает

при

t1 ≤ t ≤ t2 ,

и,

поэтому

(t)>

0 на

[t1 ,t2 ].

Отсюда

получим

(t) =ϕ

(t)

′

							′
	(ϕ (t))			+ (ψ	(t))		′
t2	′		2		′	2	ϕ (t)dt , или
l = ∫
		ϕ (t)

t1
				′

l = t∫2

dt .

(ϕ′(t))2

+ (ψ ′(t))2

(2.26)

ϕ(t1 )= a <ϕ(t2 )= b ,

Если

t1 >t2 ,

то,

учитывая, что

делаем вывод

об

убывании

ϕ(t)

отрицательности

′

на

[t2 ,t1 ].

Получаем,

что

ϕ (t)

′

ϕ (t)

= −ϕ (t), тогда

(ϕ (t))

+ (ψ (t))

′

(ϕ (t))

+ (ψ

(t))

′

ϕ (t)dt

′

l = ∫

= ∫

dt .

′

−1

(t)

Меняя пределы интегрирования, имеем

l = t∫1

dt .

(ϕ′(t))2

+ (ψ ′(t))2

(2.26')

Сравнивая формулы (2.26) и (2.26'), можно записать формулу для

вычисления l так:

l = τ∫2

dt ,

(ϕ′(t))2

+ (ψ ′(t))2

(2.27)

τ1

где τ1

и τ2

значения параметра t ,

соответствующие концам дуги, причем

τ1 <τ2 .

Пример 2.17. Найти длину астроиды, заданной параметрически уравнениями

	3
x = a cos		t,	где a >0, t [0,2π].

y = a sin3 t,

Астроида

–

замкнутая

линия,

(рис. 2.20).

Учитывая

симметрию

астроиды,

достаточно найти длину ее части, лежащей

в I четверти (t 0,

Используем

формулу

(2.27),

где

-а

ϕ(t)= a cos

t ;

(t)=3a cos

t(−sin t)

′

ψ(t)= a sin

′

t cost

и τ1

= 0

t ; ψ (t)=3a sin

(точка (а,0));

τ2

= π

(точка

(0,а)).

-а

Рис. 2.20

Получим

l = 4l1 = 4∫2

9a2 cos4 t sin2 t +9a2 sin4 t cos2 tdt = = 4∫2

dt =

9a2 cos2 t sin2 t(cos2 t + sin2 t)

π	π		cos2t	π
π	π
2	2
2	2	−		2	= − 3a(cosπ − cos0)= 6a	(ед.).
				2
=12a∫cost sintdt =6a∫sin 2tdt = 6a			2
0	0		2	0
				0

Рассмотрим теперь дугу линии на плоскости, в которой задана полярная система координат. Пусть линия – график функции ρ = f (ϕ) и полярные

углы концов дуги равны α и β , где α <β , рис. 2.21.

ϕ=β

Аϕ=α

О	1	Р	х
		Рис. 2.21

Чтобы найти длину дуги AB , введем на плоскости декартову систему координат xOy , в которой положительная полуось Ox совпадает с полярной

осью OP . Для любой точки M (x, y), лежащей на дуге, x = ρ cosϕ , y = ρ sinϕ , причем ρ = f (ϕ). Поэтому получим

x = f (ϕ)cosϕ,

y = f (ϕ)sinϕ,

т.е. кривая – это график функции, заданной параметрически, где роль параметра играет полярный угол ϕ (на дуге AB ϕ [α, β]). По формуле

(2.27)

′ 2

′

l = ∫

(f (ϕ)cosϕ)

(f (ϕ)sin ϕ)

dϕ,

и так как выражение под знаком корня равно

(f (ϕ)cosϕ + f (ϕ)(−sinϕ))

+ (f (ϕ)sinϕ + f (ϕ)cosϕ)

′

возводим суммы в квадрат и приводим подобные

= (f

′

+ (f (ϕ))

, то

(ϕ))

окончательно получаем

= ∫

(f (ϕ))

′

dϕ . (2.28)

(ϕ))

Пример 2.18. Найти длину кардиоиды, заданной в полярной системе координат уравнения ρ = a(1 − cosϕ), рис. 2.22. Учитывая

Рис. 2.22

симметрию кардиоиды, найдем длину ее половины (ϕ [0,π]) по формуле

(2.28), в которой f (ϕ)= a(1 − cosϕ), f	(ϕ)= a sinϕ , α = 0 , β =π . Имеем
	′

l = 2π∫(a(1 − cosϕ))2 + (a sinϕ)2 dϕ =

= 2aπ∫1 − 2cosϕ + cos2 ϕ + sin 2 ϕ = 2aπ∫2(1 − cosϕ)dϕ =

2 ϕ

применим формулу 1 − cosϕ = 2sin

= 4aπ∫

sin 2 ϕ

π] sin

dϕ =

при ϕ [0,

≥ 0

− cos

= 4a∫sin

dϕ =8a∫sin

=8a

=−8a cos π − cos 0 =8a (ед.).

2.1.8.4.Вычисление объема тела по площадям параллельных сечений

Рассмотрим в пространстве xOyz тело, «зажатое» между плоскостями x = a , x = b . Пусть для любого x [a,b] известна площадь сечения этого тела плоскостью, проходящей через точку x параллельно плоскости yOz

(т.е. перпендикулярно оси Ox ). Эта площадь зависит от x , т.е. является функцией, которую обозначим S(x). Пусть S(x) непрерывна на [a,b]. Нас

интересует объем данного тела. Разобьем отрезок [a,b] произвольными точками x0 = a, x1 , , xn = b на n частей и проведем через каждую точку xi


	(i = 0,1, , n )		плоскость, параллельную
	плоскости yOz (рис. 2.23).
	Тело разобьется на n слоев.
	Рассмотрим слой, лежащий между
	плоскостями		x = xi−1 и x = xi . Выберем
	на отрезке [xi−1 , xi ]			произвольную точку
	ci и для каждого			i =1, , n	построим
	цилиндр с образующей, параллельной
Рис. 2.23	оси Ox ,	и	направляющей		линией,
являющейся контуром сечения	тела плоскостью x = ci . Высота такого
цилиндра равна ∆xi = xi − xi−1 . Получим тело,		состоящее из n цилиндров,

объем которого равен сумме объемов этих цилиндров. Объем цилиндра равен V = Sосн. h , здесь для каждого i =1, , n Sосн. = S(ci ), h = ∆xi , поэтому объем i -го цилиндра равен S(ci ) ∆xi .

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 149 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20224.32 Mб4Учебное пособие 2039.pdf
#
30.04.2022327.09 Кб4Учебное пособие 204.pdf
#
30.04.20224.32 Mб4Учебное пособие 2040.pdf
#
30.04.20224.35 Mб7Учебное пособие 2042.pdf
#
30.04.20224.39 Mб5Учебное пособие 2043.pdf
#
30.04.20224.41 Mб6Учебное пособие 2044.pdf
#
30.04.20224.43 Mб21Учебное пособие 2045.pdf
#
30.04.20224.46 Mб14Учебное пособие 2046.pdf
#
30.04.20224.47 Mб24Учебное пособие 2047.pdf
#
30.04.20224.51 Mб24Учебное пособие 2049.pdf
#
30.04.2022328.36 Кб15Учебное пособие 205.pdf