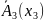Лекція 4 Множинна лінійна регресія

1. Теоретичне та емпіричне лінійні рівняння

2. Відхилення в матричній формі

3. Оператор оцінювання класичного МНК

4. Дисперсійно-коваріаційна матриця параметрів регресії

5. Множинна кореляція та детермінація

6. Тест Фішера (на адекватність моделі)

7. Перевірка гіпотез щодо параметрів багатофакторної регресії

8. Довірчі інтервали

Множинна лінійна регресія

Як правило, декілька причин є впливовими на будь-який чинник (економічний показник).

Замість парної регресії розглядається множинна

Найбільш вживана і досить проста модель множинної лінійної регресії.

Теоретичне лінійне рівняння регресії

Для індивідуальних спостережень числом n (i = 1, 2, …, n)

j-m теоретичн. коеф. регресії: характеризує чутливість Y до зміни X; або відображає вплив на умови математичного сподівання залежн. зм. Y пояснювальної зм. Хj при сталості всіх інших.

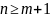оцінювання , для яких має місце найкраще наближення при спостереженнях; часткові коефіцієнти регресії

число ступенів вільності. Вважається: при оцінюванні множинною лінійною регресією для забезпечення статистичної надійності вимагається, що число спостережень щонайменше в 3 р. перевищувало число оцінюваних параметрів.

Емпіричне рівняння регресії записується

,

оцінки для ; .

Для індивідуальних значень

За даними вибірки об’єму n треба оцінити значення параметрів (параметризація моделі).

Відхилення

Скористаємося матричними позначеннями:

n – вимірний стовпець (вектор) спостережень;

Матриця n * (m+1) вимірності спостережень, i-й рядок якої відповідає спостереженням вектора значень незалеж. зм. ;

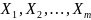Зауваження!

вектор-стовпець коефіцієнтів рівняння регресії

вектор-стовпець відхилень реальних значень yi залежної зм. Y від модельних, отриманих по рівнянню регресії.

Економетрична матрична модель записується

В матричній формі похибка записується , її квадрат має вигляд .

Результатом процедури МНК у матричній формі буде вираз

,

який називається оператором оцінювання 1 МНК, ним визначаються емпіричні коефіцієнти множинної лінійної регресії.

Зауваження. Якщо незалежні змінні в матриці Х взяти як відхилення кожного значення від свого середнього, то величина ( ) назив. матрицею моментів. Елементи її головної діагоналі є величини дисперсії незалежних змінних, інші елементи відповідають взаємним коваріаціям.

В матричній формі похибка записується утворимо квадрат похибки

,

де індекс Т – транспонування; матричні співвідношення:

відомі.

Умова існування extr:

Якщо незалежні змінні в матриці Х взяті як відхилення кожного значення від свого середнього, то матрицю назив. матрицю моментів.

Структура матриці моментів відбивав зв’язки між незалеж. змінними.

Зауваження. Вираз назив. оператором оцінювання 1 МНК, тобто ним визначаються емпіричні коеф. множинної лінійної регресії.

Дисперсійно-коваріаційна матриця параметрів регресії (оцінок параметрів моделі) записується

На головній діагоналі матриці містяться оцінки дисперсії параметрів, інші її елементи відображають оцінки коваріації між bj та bk параметрами.

Має місце

,

де дисперсія ВВ її формули

Нехай Cjk елемент матриці , на перетині j-го рядка і k-го стовпця. Тоді елементи головної діагоналі дисперсійної матриці обчислюються як 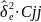, інші її елементи як .

Стандартні помилки оцінок параметрів моделі є

У випадку лінійної регресії коефіцієнт детермінації дорівнює квадратної вибіркового коефіцієнта кореляції між двома рядами спостережень – експериментальними значеннями регресанда (yi) і його розрахункового .

.

Враховано, що класич. регрес. моделі .

Мірою ступеня відповідності модельних даних фактичним (і- 1, 1,… n) є коефіцієнт множинної кореляції

R= Для класичної регресійної моделі

Його квадрат є коефіцієнтом множинної детермінації

<≡

Як у випадку простої лінійної регресії: SST=SSE+SSR<=>

=1= ≡

При зростанні кількості факторів також ↑ і ніколи не зменшується.

Розглядається оцінений коефіцієнт детермінації

(скориговані на їхні ступені вільності)

Суми квадратів у чисельнику та знаменнику діляться на відповідні ступені вільності, в яких ураховується число факторів моделі

Має місце формула (k>1; ).

Якщо кількість факторів ↑, то оцінений коефіцієнт детермінації ↑ повільніше, ніж . Цим користуються при порівнянні різних регресійних моделей.

Перевірка моделі на адекватність за F-критерієм Фішера

Нульова гіпотеза Н₀: =0 (j=1…m) <=> H₀:

Проти альтернативної Н₁: хоча б одне =0

Для перевірки Н₀ гіпотези розраховується F-статистика Фішера з m та

(n-m-1) ступенями вільності

, де -число факторів; - число спостережень.

За F-таблицями Фішера шукається критичне значення з та α-рівнем помилки (або (1-α)100% рівнем довіри).

Якщо F > , то нуль-гіпотеза відкидається; модель адекватна. У протилежному випадку нульова гіпотеза приймається, модель неадекватна.

F-тест, який є мірою адекватності регресійної моделі, також виступає мірою статистичної значущості коефіцієнта детермінації.

Зауваження! F-відношення Фішера (статистика) розраховується на підставі формули:

F= , k=m+1

За F-таблицями Фішера шукається (k-1; n-k; α- рівень помилки)

Якщо F > (k-1; n-k; α), тоді Н відкидається; у протилежному випадку приймається. Таким чином, тестування на адекватність моделі за допомогою тільки коефіцієнтів детермінації.

Перевірка гіпотез щодо параметрів багатофакторної регресії у матричному вигляді

Кожний параметр відповідає В~Ɲ [β, нормальний закон розподілу, де β- матем. сподівання=параметру узагальненої регр.моделі

Заміна справжнього значення дисперсії ВВ на його оцінку приводить до того, що Ʉ елемент вектора В відповідає t-розподілу Стьюдента з (n-k) ступенями вільності.

Задаємось α*100% рівнем значимості; для кожного параметра окремо будується t-статистика

t = з (n-k) ступенями вільності, де - оцінка параметра ; - гіпотетичне значення, яке має прийняти ; - оцінка дисперсії параметра (з регресії); n- кількість спостережень; k- загальна кількість оцінених параметрів.

В економетриці поширеною формулою нуль-гіпотези є така:

Н₀: = 0.

t-статистика є = її значення порівнюються з табличним, яке дає змогу знайти критичну зону з (n-k) ступенями вільності.

Якщо потрапляє не у критичну зону, то з ймовірністю (1-α) 100% оцінка є статистично незначима (Н₀ приймається)

В протилежному випадку – Н₀ відкидається.

Зауваження! = є відношення до оцінки свого стандартного відхилення (середнього квадратичного).

Після перевірки адекватності моделі та значимості знайдених параметрів за t-критерієм Стьюдента виконуються прогнози, будуються інтервали довіри, вивчається вплив окремих факторів на залежний чинник.

По аналогії з процедурою тестування нуль-гіпотези для параметрів за t-тестом Стьюдента інтервали довіри записуються

= ± .

Побудова довірчих інтервалів: для математичного сподівання залежної змінної з рівнем довіри (1-α) 100% здійснюється за формулою

Або в матричній формі

<= M (Y│X₀) <= ,

Де = Х₀В розглядається як точкова оцінка математичного сподівання прогнозного значення Y₀, а також як індивідуальне значення Y₀ для вектора незалежної мінної Х₀, що лежить за межами базового періоду.

Для індивідуального значення залежної змінної

<= Y₀<= ;

В координатній формі

.

Мультиколінеарність

Визначається як лінійний взаємозв’язок 2ох або декількох пояснювальних змінних: (вони мають високий ступінь кореляції, тобто →1 для і = j), розрізняють так звану недосконалу колінеарність, що реально має місце. При наявності функціональної залежності між змінними є досконала мультиколінеарність (теоретично ᴲ, рідкісний випадок).

Практичні наслідки мультиколінеарності:

1. Великі дисперсії (стандартні похибки) оцінок за МНК. Цим самим утруднюється знаходження істинних значень, розширюються інтервальні оцінки, падає їх точність.

2. Зменшуються t-статистики коефіцієнтів, що може привести до хибного висновку про істотність впливу відповідної пояснювальної змінної на залежну.

3. Оцінки коефіцієнтів по МНК та їх стандартні похибки стають дуже чутливими до малих змін даних (нестійкі)

Наявність мультиколінеарності

Єдиного методу або надійних методів тестування колінеарності ᴲ

Найповніше дослідження здійснюється алгоритмом Фаррара-Глобера.

Він містить 3 види статистичних критеріїв, на підставі яких перевіряється мультиколінеарність:

• Усього масиву незалежних змінних ( 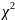-критерій);

• Кожної незалежної змінної з усіма іншими (F-критерій);

• Кожної пари незалежних змінних (t-критерій)

Кроки алгоритму Фаррара-Глобера

Нормалізувати змінні , ,…, економетричної моделі, для чого обчислити

= ,

де n – число спостережень (і=1,2,… n); m – число незалежних змінних (j= )

Інші ознаки мультиколінеарності:

1. Найкращою ознакою є високе значення коефіцієнта детермінації при незначимості параметрів за t-тестом.

2. У моделі з 2ма змінними найкращою ознакою є значення простого коефіцієнта кореляції.

3. У моделі з більш як двома змінними простий коефіцієнт кореляції може бути низький при наявності мультиколінеарності, до уваги беруться часткові коефіцієнти кореляції.

4. Якщо коефіцієнти детермінації великий, а часткові коефіцієнти кореляції низькі, то мультиколінеарність можлива.(є надлишкові змінні)

При високих коефіцієнтах детермінації і часткових коефіцієнтах кореляції не завжди можна виявити мультиколінеарність.

Гетероскедастичність

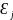Одна з ключових умов МНК – гомоскедастичність: Д( )=Д( )= =Const

Ʉ i, j – дисперсія кожної випадкової величини стала.

Графічно для простої лінійної регресії

• Постійність дисперсій відхилень порушується – гетероскедастичність: Д( )=var( )= =Const

• Графічно 3 різні види явища гетероскедастичності:

Наслідки гетероскедастичності

Раніше говорилось про BLUE оцінки МНК при виконанні умов теорії Гаусса-Маркова.

1. Оцінки коефіцієнтів незміщені і лінійні, але

2. Оцінки неефективні. Збільшення дисперсії оцінок знижується ймовірність отримання максимально точних оцінок.

3. Дисперсії оцінок будуть розраховуватися зі зміщенням. (Непояснювана рівнянням регресії дисперсія = , m є число пояснювальних змінних, сама є зсунутою)

4. Висновки на підставі t- та F- статистик будуть ненадійні, інтервальні оцінки також. (Можуть визнаватися статистично значущими коефіцієнти, котрі не є такими)

Зауваження. Пояснення неефективності оцінок МНК при гетероскедастичності.

=

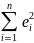Параметричний тест Гольдфельда-Квандта

Для невеликої сукупності спостережень в припущенні, що дисперсія залишків ↑ пропорційно до квадрата однієї з незалежних змінних моделі, тобто М( )= * . (Похибки регресії вважаються нормальнорозподіленими)

Крок1.

Спостереження ( вихідні дано впорядкувати відповідно до величин елементів вектора , який може викликати зміну дисперсії залишків.

Крок2.

Відкинути числом С спостереження, які знаходяться всередині векторів вихідних даних, де С= , n – кількість елементів вектора .

Крок3.

Побудувати 2 економетричні моделі за допомогою 1 МНК (для двох утворених сукупностей спостережень обсягом кожна за умови ˃=m (m– кількість змінних), причому одна підвибірка включає малі значення Х, друга – великі).

Крок 4.

Обчислити суму квадратів залишків: = для підвибірки з малими значеннями ; = – відповідно для другої підвибірки.

Крок 5.

5.1. Розрахувати величину R=S2/S1, яка при виконанні гіпотези, про гомоскедастичність відповідатиме F-розподілу зі ступенями вільності

5.2. Значення критерію R порівнюється з табличним значенням F-критерію при α і величинах : якщо , то гетероскедастичність відсутня.

Зауваження. Чим більша R, тим більша гетероскедастичність.

Метод Ейткена (узагальнений МНК)

де матриця S має вигляд

(коваріація відсутня)

залежить від гіпотези що дисперсії залишків.

Тоді оператор оцінювання записується

Матриця коваріацій

;

Алгоритм Ейткена для оцінювання параметрів економетричної моделі з автокореляційними залишками шукається:

1. Оцінка параметрів моделі за 1 МНК. Використовують 1 МНК.

2. Досліджуються залишків на предмет автокореляції (застосовуються критерії DW).

3. Формується матриця коваріації залишків V або S.

симетр.

Кожен її елемент виражає коеф. автокореляції відповідного порядку для залишків 2t.

Автокореляція

Вона наявна, коли ВВ залежні собою, тобто M( для і.

Послідовн. кореляція визначається кореляція між спостережуваними показниками, упорядкованими в або просторі.

В економ. задачах має місце додатна автокореляція частіше, ніж від’ємна.

Автокореляцією називають залежність між значеннями однієї вибірки із запізненням в один …: для є залежність.

У випадку ƎL залежності між значенням різницю вибірок.

має місце серійна кореляція.

Основні причини явища автокореляції: інерційність та циклічність економ. процесів; похибки специфікації; ефект павутини (реакція економ. чинників на зміну економ. умов відбувається із запізненням); вирівнювання даних.

Автокореляція залишків: їх дисперсія стала, але спостерігається їх коваріація.

Наслідки автокореляції (в разі застосування 1 МНК класичного):

1. Оцінки параметрів лінійні, незміщені, але неефективні.

2. Дисперсії оцінок зміщені (часто занижені, ростуть t-статистики).

3. Оцінка дисперсії регресії зміщена, занижена.

4. Гіршають прогнозні якості моделі (висновки по t-i F-статистиках невірні).

Тест Дарбіна-Уотсона

Найбільш відомий, поширений для перевірки моделі на наявність кореляції між залишками.

Для малих вибірок

Етапи:

1. Розраховується значення d-статистики за формулою:

; відомо, що .

2. Вказується α; підраховується кількість факторів (k) з досліджуваній моделі. Нехай k=p за табл. Дарбіна-Уотсона при α; p; і кількості спостережень n (або T) знаходимо два значення dL і dU.

3. Якщо розраховане значення d-статистики знаходиться в проміжку від 0 до dL (0 < d < dL), то це свідчить про наявність позитивної автокореляції.

Для обчислення ƍ використати циклічний коеф. кореляції, а саме ƍ = r; але r коригується на величину зміщення, тобто

Ut – величина залишків у період t;

m – число незалежн. змінних.

4. …

5. Оцінка параметрів за формулою здійснюється , Х матриця незалежних змін. (пояснювальних).

Якщо dL ≤ d ≤ dU, тобто значення d потрапляє в зону невизначеності або 4-dU ≤ d ≤ 4-dL, то не можемо зробити висновок ні про наявність ні про відсутність автокореляції.

Якщо 4-dL < d < 4, то негативна автокореляція.

Якщо dU < d < 4-dU, то нема автокореляції.

Обмеження у застосуванні критерію Дарбіна-Уотсона

1. Застосований до моделей, що мають вільний член b0

2. Випадкові відхилення визначаються ітеративно: (так звана авторегресійна схема 1-го порядку AR(1)).

3. Статистичні дані однакової періодичності (без пропусків в спостереженнях).

4. Критерій не застосований до авторегресійних моделей виду

Лекція 6 (1)

Основи лінійного програмування

Чому математичне програмування?

1959 р. – дата появи цього терміну. Назва пояснюється вибором програми дій (наших вчинків) для досягнення мети (розв’язання задачі). Бажано ціль досягати якнайшвидше – результат раціональних, цілеспрямованих дій або оптимальної програми дій: тут використовуються математичні методи розв’язання задач, знаходження extr функції на множинах з обмеженнями.

Традиційно вважається, що лінійне програмування (ЛП) є серцевина математичної підготовки економістів.

Зауваження! Слушно прийняти до уваги, що дане твердження з’явилося в епоху домінування теорії рівноважного стану.

Постановка задачі ЛП: економічний зміст, її математична модель (ММ)

а) Вербальне формулювання задачі ЛП

На випуск n видів продукції П₁, , … витрачається m m видів ресурсів (сировина, матеріали, трудові ресурси тощо) А₁, ,… .

Відомі витрати ресурсів і-го виду на одиницю продукції j-го виду, обсяг ресурсів і-го виду та величина прибутку від реалізації одиниці продукції j-го виду. Треба так організувати випуск продукції, виходячи із наявних ресурсів, щоб одержувати найбільший прибуток.

Словесно формулювання задачі відображено в таблиці та оцінка ресурсів наводиться в таблиці.

б) Табличний спосіб запису задачі ЛП

Види ресурсів	Види продукції						Запаси ресурсів
	П₁
А₁ - -	- -	- -	- - - - - -	- -	- - - - - -	- -	- -
Випуск продукції			-		-
Прибуток від одиниці продукції			-		-

Від табличного способу подання інформації перейдемо до аналітичного, тобто запишемо рівняння ММ.

Змінні х₁, , … – кількість одиниць випущеної продукції відповідно П₁, , …

в) Аналітичний запис задачі ЛП

Фактичні витрати відповідного виду не можуть перевищувати наявний їх обсяг (*)

(**)Із економічного змісту: 0, 0, … 0. Прибуток складає від випуску всієї продукції (***)ᵶ= + →max, зрозуміло.

Система нерівностей (*) і (**) та лінійна форма (***) або функція мети, цільова функція визначає ММ задачі.

Від координатної розгорнутої форми запису задачі лінійного програмування (ЗЛП) перейдемо до компактної матричної

→ extr (max або min)

(i=1, 2,…,m)

0 (j=1,2,…,n)

загальноприйнятої у літературі.

Форми запису задачі ЛП

Існують три: загальна

→ extr (max або min)

(i=1, 2,…, )

(i= 1,…,m)

0 (j=1,2,…,n),

яка зручна для теоретичних досліджень;

Стандартна

→ extr

(i=1, 2,…,m)

0 (j=1,2,…,n),

до якої зводяться більшість задач практики;

Канонічна

→ extr

(i=1, 2,…,m)

0 (j=1,2,…,n),

яка використовується при чисельному розв’язанні задач ЛП.

Чим відрізняються наведені вище форми запису задачі ЛП?

Загальна передбачає мішану сукупність рівнянь і нерівностей; стандартна – тільки нерівностей одного сенсу (в одну сторону); канонічна – тільки рівності, зберігаючи умову >=0 .

!Як здійснюється перехід від стандартної форми канонічної?

від « » перехід до «=» через + додаткові змінні

від « » перехід до «=» через – додаткові змінні

Різновиди запису канонічної форми задачі ЛП

Система обмежень переписується у векторному вигляді

+ +…+ … = ,

де = є вектор стовпець умов затрат, Т-індекс транспортування;

є вектор обмежень (запасів).

!Тоді вектор обмежень є розвинення в базисі векторів затрат, – коефіцієнти розвинення.

Задача ЛП формулюється: знайти точки =( ) з невід’ємними координатами 0 такі, що виконується

+…+ … = ,

причому лінійна форма ᵶ≡f(x)=c₁ +…+ досягає екстремуму extr (max f або min f).

Канонічна форма задачі ЛП з використанням матрично-векторного запису формулюється: знайти ᵶ max (min)= при умові А = , де 0, причому = є вектор-строка; = є вектор-стовпець; А= ( ), i=1, 2,…,m; j=1,2,…,n є матриця системи обмежень; – вектор стовпець обмежень; – нуль-вектор.

Термінологія

• Обмеження (i= ) в економіці називаються лімітами.

• Набір змінних таких, що матриця, складена із коефіцієнтів біля цих змінних буде невироджена (det A ≠ 0), утворює базис; самі змінні називаються базисними.

• Розв’язки з невід’ємними значеннями змінних, тобто 0, будуть допустимими.

Геометрично базисні розв’язки є вершини многогранника умов – області М задачі ЛП (випадок 2-ох змінних).

Оптимальним розв’язком задачі ЛП називається сукупність чисел {х₁, х₂, …, х_n}, що задовольняє умовам задачі і лінійна форма досягає екстремуму.

Для економістів розв’язок = план.

План називається базисним, якщо вектори розвинення для являються лінійно незалежними.

Кожен план відповідає деякій точці ОДЗ (многогранника умов). Плани, що відповідають вершинам ОДЗ називаються опорними.

Геометричне (графічне) розв’язання ЗЛП

В окремому випадку двовимірного простору економічних подій (розглядаються лише два економічних фактори) ММ задачі ЛП записується і формується так: знайти вектор-план Х={x₁, x₂} що задовольняє обмеженням – системі нерівностей

,

і надає екстремального (extr) значення (мінімального min або максимального max) лінійній функції – цільовій або функції мети (лінія рівня).

Зауваження. У випадку рівності кожне відношення для обмеження (*) є пряма на координатній площині.

Кожна пряма L: розділяє координатну площину на дві напівплощини – додатну та від’ємну: відповідно всі точки > V точки < b (під прямою). Вектор нормалі вказує на це.

Нагадаємо знаки квадратичної координатної площини х₁Ох₂ – простору економічних подій.

Вектор нормалі (або grad z – градієнт) лінійної функції вказує напрямок її зростання.

Область допустимих значень (ОДЗ) визначається системою нерівностей (*): завжди розташована у 1-му квадранті і може бути многогранником замкненим або відкритою областю М.

Щодо побудови області М

Перетин напівплощин, визначуваних нерівностями системи обмежень, може давати:

Лінія рівнів є пряма , що проходить через початок координат і пересовується паралельно самій собі в напрямку grad z.

Геометричне формулювання задачі ЛП: серед всіх точок обл. М відшукати таку, щоб лінія рівнів z (функція мети) приймала: найменше значення (z_min) – це 1-а М; найбільше значення (z_max) – остання точка зустрічі за умови паралельного переносу лінії нульового рівня z₀ самій собі в бік grad z.

Взаємне розташування області допустимих розв’язків (ОДЗ) і лінії рівнів (z₀)

Нескінченна множина розв’язків або альтернативний оптимум (min).

Приклад 1. Знайти max цільової функції 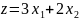для системи обмежень:

Крок 1. Будується ОДЗ:

Крок 2. Будується лінія нульового рівня:

Вона пересувається || самій собі в напрямку grad z. Остання точка перетину лінії рівня з областю М відповідає z_max.

Крок 3.

Інший спосіб розв’язання. Обчислити: координати усіх вершин многогранника; значення z у вершинах області М; вибрати найбільше числове значення.

Короткий зміст теорії ЛП

Лема1. Множина розв’язків системи обмежень задачі ЛП опукла.

Опуклим тілом називається таке, якому разом з довільними його точками належить і весь відрізок, що з’єднує ці точки.

Приклади: круг; еліпс; ; ; паралелепіпед; площина є випукла фігура ( область) не є випуклою.

Лема2. Перетин 2-ох опуклих множин є опукла множина.

Лема3. Множина планів задачі ЛП опукла.

Теорема 1. Випукла лінійна комбінація кутових точок випуклого обмеженого многогранника умов (конуса К) не виходть за нього.

Приклад:

Вектори λ₁, + = утворюють лінійну комбінацію і лежать в куту, який називається конусом К.

При умові λ₁+ =1 буде випукла лінійна комбінація, причому λ₁= λ, =1-λ і λє(0,1): множині всіх випуклих комбінацій векторів відповідає прямолінійний відрізок кінців цих векторів.

Якщо такими є вершини многогранника, то згадуваному відрізку відповідає ребро.

Теорема 2. Extr лінійної форми досягається в кутовій точці конуса К.

Теорема 3. Якщо існує множина лінійно незалежних векторів ... таких, що виконується х₁ +…+ +…+ =

Для Ʉ 0 (j=1,2…r), то точка = ; 0, 0,…0} є кутова для випуклої множини К розв’язків системи обмежень задачі ЛП.

Теорема 4. (обернена до теор.3). Якщо = ; 0, 0,…0} кутова точка множини К, то існують лінійно незалежні вектори ... такі, що має місце +…+ +…+ = для 0 (j=1,2…r)

Лекція 6 (2)

Числові розв’язування задачі лінійного програмування(ЛП)

План:

1. Симплекс-алгоритм розв’язування задачі ЛП:

А)Початкова симплекс-таблиця;

Б)Правила утворення наступної симплекс-таблиці.

2.Умови застосування класичного симплекс-метода.

3.Дослідження задачі ЛП.

4.Метод штучного базису.

5.Елементи теорії задачі ЛП.

Симплекс-таблиця задачі ЛП

Стандартна форма задачі:

-2x₁+x₂≤2;

x₁-2x₂≤2;

x₁+x₂≤5;

x₁≥0;

x₂≥0.

Z=(-x₁+x₂)  min,

для обмежень:

Канонічна форма задачі:

Z= -x₁+x₂+0*x₃+0*x₄+0*x₅min

додаткові змінні

-2x₁+x₂+x₃=2;

x₁-2x₂+0*x₃+x₄=2;

x₁+x₂+0*x₃+0*x₄+x₅=5;

x_j ≥0, де j=1, 2, ... ,5.

Інша форма запису канонічної задачі ЛП:

= , де

Табличне відображення:

СБj	або xj		-1	1	0	0	0
0	x3	2	-2	1	1	0	0
0	x4	2	1	-2	0	1	0
0	x5	5	1	1	0	0	1
Індексна строка ↔∆j		0 ∆0	1 ∆1	-1 ∆2	0 ∆3	0 ∆4	0 ∆5

Перший базисний розв’язок:

= (x₁; x₂; x₃; x₄; x₅) ≡ (0; 0; 2; 2; 5),

мовою економіки - нічого не виробляється.

Таблиця

СBj	(xj)		-1	1	0	0	0
0	x3	2	-2	1	1	0	0
0	x4	2	1	-2	0	1	0
0	x5	5	1	1	0	0	1
Індексна строка ∆j		0 ∆0	1 ∆1	-1 ∆2	0 ∆3	0 ∆4	∆5

Першу колонку С_Bj складають коефіцієнти цільової функції біля базисних змінних.

Друга колонка є базисні змінні.

Третя колонка відповідає координатам (обмеженням ресурсів).

Наступні 5 колонок відповідають коефіцієнтам біля невідомих системи обмежень, причому над стовпцями стоять коефіцієнти функції мети.

Як заповнюється індексна строка?

Величина = * є значення лінійної форми для початкового опорного плану;

відповідно = * ,- є числові оцінки вільних змінних.

Застосовується симплекс-алгоритм.

Розв’язок або опорний план буде оптимальний тоді, коли :

• Для задачі ЛП на min усі оцінки недодатні, тобто від’ємні або

• Для задачі ЛП на max усі величини невід’ємні , тобто додатні або 0

Умови застосування класичного симплекс-метода

1. Задача ЛП записується в канонічній формі

2. Для матриці системи обмежень (m рядків, n стовпців)  {\displaystyle \operatorname {rang} A}rangA=m, тобто всі рядки лінійно незалежні

3. Координати вектора запасів додатні

4. Відомий початковий базисний розв’язок

5. Усі допустимі базисні розв’язки (опорні плани) є всевироджені (базисні змінні≠0)

Дослідження задачі ЛП2

Симплекс-методом одночасно досліджується розв’язувана задача:

1. Опорний план (розв’язок) єдиний; коли серед величин – симплекс-різниць оптимального плану нульовими є лише базисні;

2. Немає розв’язку, коли система обмежень несумісна, що з’ясовується в процесі пошуку початкового базисного розв’язку (опорного плану);

3. Якщо в симплекс-таблиці задачі ЛП на max для деякої величини усі елементи k-го стовпця недодатні, тобто розв’язку немає, бо цільова функція необмежена зверху (у випадку задачі ЛП на min має місце і елементи k-го стовпця від’ємні, цільова функція необмежена знизу)

4. Коли серед величин індексної строки нульовими є не тільки базисні, а також інша .

Альтернативний оптимизм

Для задачі ЛП:

має місце симплекс-таблиця:

СБj	Базис змінних		1	1	0	0
			x1	x2	x3	x4
0 0	x3	2 12 0	1 4 -1	1 3 -1	1 0 0	0 1 0
	x4
	σj
1 0	x1	2 4 2	1 0 0	1 -1 0	1 -4 1	0 1 0
	x4
	σj
1 0	x2	2 6 2	1 1 0	1 0 0	1 -3 1	0 1 0
	x4
	σj

На 2-ій ітерації досягли оптимального розв’язку

Але серед величин нульовими є не тільки базисні також небазисної .

Утворюється ще одна симплекс – таблиця (третя, остання), вводячи в базис замість :

Довільна оцінка лінійна комбінація оптимальних розв'язків також буде розв'язком задачі, що записується:

, де

ЗАУВАЖЕННЯ! Інший вигляд формули обчислення коефіцієнтів індексної строки:

Метод штучного базису (М-задача)

Застосовується там, де початковий базис безпосередньо не встановлюється (в обмеженнях не виділяється одинична матриця)

Приклад 1:

Жодного одиничного вектора.

Вводяться штучні змінні : стільки їх, скільки рівнянь в обмеженнях задачі ЛП. Цим самим утворюється базис. Оскільки задача ЛП на мінімізація лінійної форми, то в ній штучні змінні присутні з коефіцієнтами M>0, М досить велике число (для задачі на max число М<0). Таким чином, будується розширена задача( М-задача):

;

;

x_j ≥0, де j=1, 2, ... ,7.

Вона розв’язується симплексним методом. Якщо в такому розвязку всі штучні змінні=0, то є оптимальний план. Якщо хоча б одна штучна змінна в отриманому розв’язку ≠0,то не існує розвязку( оптимального плану початкової задачі.)

Приклад 2: max (5 );

=3

=3; Xj≥0, j=1…4

Нема одиничних векторів. Через штучні змінні i утворюється М-задача:

;

x_j ≥0, де j=1, 2, ... ,6.

Базові змінні	СБj		5	3	4	-1	-M	-M
			x1	x2	x3	x4	x5	x6
x5	-M	3	1	3	2	2	1	0
x6	-M	3	2	2	1	1	0	1
	(m+1)	0	-5	-3	-4	1	0	0
	(m+2)	-6M	-3M	-5M	-3M	-3M	0	0

В М- задачі ідексна строка зображується рядками: в першому (m+1) записується вільні члени виразів

i ;

В другому рядку (m+2) записуються коефіцієнти з величинами M.

ЗАУВАЖЕННЯ! Поки не виключені з базису штучні змінні, критерієм оптимальності служитиме рядок (m+2) індексної строки.

Продовження таблиці

Базові змінні	СБj		5	3	4	-1	-M	-M
			x1	x2	x3	x4	x5	x6
x2 x6	3 -M (m+1) (m+2)	1 1 3 -M	1/3 4/3 -4 -4/3M	1 0 0 0	2/3 -1/3 -2 1/3M	2/3 -1/3 3 1/3M	1/3 -2/3 1 5/3M	0 1 0 0
x2 x1	3 5 (m+1) (m+2)	3/4 3/4 6 6	0 1 0 0	1 0 0 0	3/4 -1/4 -3 -3	3/4 -1/4 2 2	1/2 -1/2 -1 -1	-1/4 3/4 3 3
x3 x1	4 5	1 1 9	0 1 0	4/3 1/3 4	1 1 0	1 0 5	2/3 -1/3 1	-1/3 2/3 2

X₂

Теорема 1. Випукла лінійна комбінація кутових точок обмеженого многогранника умов (конуса К) не виходить за нього.

Приклад

Нехай

X₁

0

Вектори утворюють лінійну комбінацію і лежить в куту, який називається конусом К. При умові буде випукла лінійна комбінація, причому , і є (0,1): множині всіх випуклих комбінацій векторів і відповідає прямолінійний відрізок кінців цих векторів.

Якщо такими є вершини багатогранника, то кінцевий згадуваному відрізку відповідає ребро.

Теорема 2.

Extr лінійної форми досягається в кутовий точці конуса К. (ОДЗ)

Теорема 3. Якщо існує множина лінійно незалежних векторів таких, що виконується

Для , то точка є кутова для випуклої множини К розв’язків системи обмежень задачі ЛП.

Теорема 4. (обернена до теор.3). Якщо кутова точка множини К, то існують лінійно незалежні вектори такі, що має місце

для