Федеральное агентство связи

Ордена Трудового Красного Знамени федеральное государственное бюджетное

образовательное учреждение высшего образования

“Московский технический университет связи и информатики”

Кафедра информатики

ЛАБОРАТОРНАЯ РАБОТА №1

«Методы решения нелинейных уравнений»

по дисциплине

Численные методы

Выполнил: студент гр. БИН1907 Власов Андрей

Проверил: к.т.н., доцент Г.Сосновиков

Москва 2021 г.

ОГЛАВЛЕНИЕ

I. ЗАДАНИЕ

Общее задание, индивидуальный вариант 3

II. ВЫПОЛНЕНИЕ РАБОТЫ

Выполнение 4-9

I. ЗАДАНИЕ

Общее задание к работе

1. Выбрать индивидуальное задание из табл.:

• нелинейное уравнение;

• методы решения нелинейного уравнения для выполнения 3-х итераций;

2. Отделить корни заданного уравнения графическим и аналитическим

методом

3. Для каждого из заданных методов провести исследование функции

нелинейного уравнения:

• проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;

• выбрать начальное приближение к корню;

• сформулировать условие окончания этапа уточнения корня.

4. С использованием итерационной формуле 1-го заданного методу

провести расчет трех итераций с использованием средств пакета Scilab.

5. Оценить погрешность результата после 3-х итераций.

6. Для 2-го заданного метода выполнить решение уравнения с точностью

10^ -4, создав программу, реализующую заданный метод. Произвести

расчет, а результаты решений свести в табл. 1-2.

7. Найти решение нелинейного уравнения на отделенном отрезке с

использованием функции fsolve пакета Scilab.

Индивидуальный вариант задания

Рисунок 1 – Индивидуальный вариант №1 с методом половинного деления(1) и методом хорд(4)

II. ВЫПОЛНЕНИЕ РАБОТЫ

Результат отделения корней:

--> deff('y=f(x)','y=x-cos(x./3)');

--> X=0:1;

--> Y=f(X);

--> plot2d(X,Y)

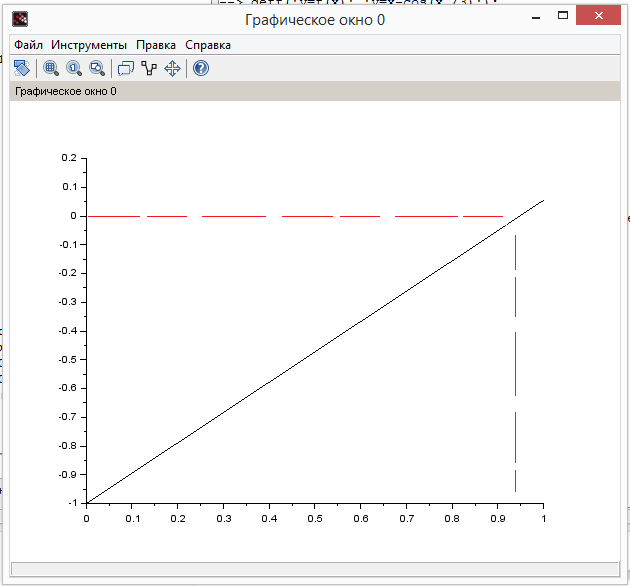
Рисунок 2 – График функции x-cos(x./3) при x принадлежит отрезку от 0 до 1

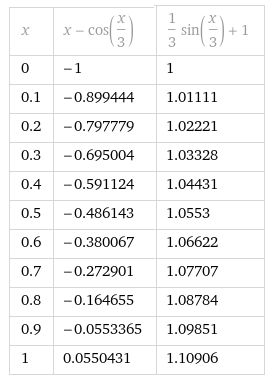
Рисунок 3 – Таблица значений функции x-cos(x./3) и ее производной (sin(x./3))./3+1

Вывод: На концах отрезка [0;1] функция имеет противоположные

знаки, а 1-я производная знакопостоянна, следовательно, на этом отрезке

уравнение x-cos(x./3) имеет единственный корень.

Метод половинного деления (1)

Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [0;1] функция f(x)= x-cos(x./3) меняет знак (f(0)*f(1)<0) и монотонна, то условие сходимости выполняется.

1) Уточним корень уравнения x-cos(x./3)=0 с точностью ε=0.1, который локализован на отрезке [0;1] с помощью метода половинного деления (1).

Начальным приближением является середина отрезка [0;1];

//Файл lab1.sce - Сценарий для проведения расчета 3-х итераций по методу

//половинного деления

function ff=f(x)

ff=x-cos(x./3);

endfunction

// Расчет 3-х итераций по методу половинного деления

disp(' n a b f(a) f(b) c=(a+b)/2 f(c) b-a'); // Вывод первой строки таблицы

n=0; fa=f(a);fb=f(b);c=(a+b)/2; fc=f(c); z=[n,a,b,fa,fb,c,fc,b-a];

disp(z); // Промежуточный результат

for n=1:3

if f(c)*f(a)<0 then b=c; else a=c; end

fa=f(a);fb=f(b);c=(a+b)/2; fc=f(c); z=[n,a,b,fa,fb,c,fc,b-a];

disp(z); // Промежуточный результат

c=(a+b)/2; // Приближение

end

//Конец сценария lab1.sce Ввод левой и правой границы (a,b)

// Запуск файла lab1.sce

--> a=0;b=1; // Ввод левой и правой границы (a,b)

--> exec('C:\Users\Admin\Desktop\lab1.sce', -1)

" n a b f(a) f(b) c=(a+b)/2 f(c) b-a"

0. 0. 1. -1. 0.0550431 0.5 -0.4861432 1.

1. 0.5 1. -0.4861432 0.0550431 0.75 -0.2189124 0.5

2. 0.75 1. -0.2189124 0.0550431 0.875 -0.082766 0.25

column 1 to 7

3. 0.875 1. -0.082766 0.0550431 0.9375 -0.0140679

column 8

0.125

После трех итераций приближение к корню x3=0.9375

Погрешность результата, полученного после 3-х итераций равна 0.125

Метод хорд (4)

Рисунок 4 - Таблица значений второй производной функции x-cos(x./3)

Для сходимости метода необходимо знакопостоянство f’’(x) на отрезке [a;b].

Вид рекуррентной формулы зависит от того, какая из точек a или b является неподвижной. Неподвижен тот конец отрезка [a;b] , для которого знак функции f(x) совпадает со знаком ее второй производной. Тогда второй конец отрезка можно принять за начальное приближение к корню, то есть точку х0.

Выше было показано, что для функции f(x)= x-cos(x./3) f’’(x) на отрезке [0;1] неподвижной точкой является точка x=b=1, так как f’’(x)*f(1)>0.

Таким образом, полагая x0=a=0, получим сходящуюся последовательность приближений к корню.

В рассматриваемой задаче рекуррентная формула принимает следующий вид

//Файл lab2.sce - Сценарий для проведения расчета по методу хорд

function ff=f(x) //Левая часть уравнения

ff=x-cos(x./3);

endfunction;

disp(' n x f(x)')

n=0; x=0; fx=f(x); z=[n,x,fx];

disp(z);

for n=1:3

x=x-f(x)/(f(xx)-f(x))*(xx-x); fx=f(x); z=[n,x,fx]

disp(z); //вывод результата

end

//Конец сценария lab2.sce

--> xx = 1; //Ввод неподвижной точки x=b=1

--> exec('C:\Users\Admin\Desktop\lab2.sce', -1) // Запуск файла lab2.sce

" n x f(x)"

0. 0. -1.

1. 0.9478286 -0.0026752

2. 0.9502467 -0.0000063

3. 0.9502525 -1.502D-08

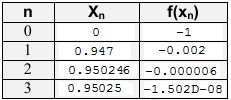
Оценим погрешность по формуле:

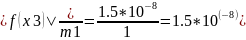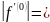, где m1= 1

Решение нелинейного уравнения с использованием функции

пакета Scilab fsolve

--> deff('[y]=f(x)', 'y= x-cos(x./3) ';)

--> x(1)=fsolve(1,f);

--> x

x =

0.9502525