
- •Часть 1
- •Введение
- •1. Особенности машинной арифметики, точность вычислений на эвм (Лабораторная работа №1)
- •2. Изучение понятия Обусловленности вычислительной задачи (Лабораторная работа №2)
- •3. Решение нелинейных уравнений
- •3.1. Общие сведения
- •3.2. Метод бисекции (Лабораторная работа №3)
- •3.3. Метод хорд (Лабораторная работа №4)
- •3.4. Метод Ньютона (Лабораторная работа № 5)
- •3.5. Метод простых итераций (Лабораторная работа №6)
- •3.6. Курсовая работа по дисциплине и варианты заданий
- •4. Численное интегрирование
- •4.1. Составные формулы прямоугольников, трапеций, Симпсона. (Лабораторная работа №6)
- •4.2. Формула Гаусса. (Лабораторная работа №7)
- •Библиографический список
- •1. Особенности машинной арифметики, точность вычислений на эвм 5
3.3. Метод хорд (Лабораторная работа №4)
Пусть найден отрезок [a, b], на котором функция
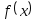 меняет
знак. Для определенности положим
меняет
знак. Для определенности положим
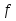 (a)>0,
(a)>0,
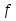 (b)<0.
В методе хорд
процесс итераций состоит в том, что в
качестве приближений к корню уравнения
(b)<0.
В методе хорд
процесс итераций состоит в том, что в
качестве приближений к корню уравнения
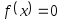 принимаются значенияc0,
c1,
.
. .
точек пересечения хорды с осью абсцисс,
как это показано на рис.1.
принимаются значенияc0,
c1,
.
. .
точек пересечения хорды с осью абсцисс,
как это показано на рис.1.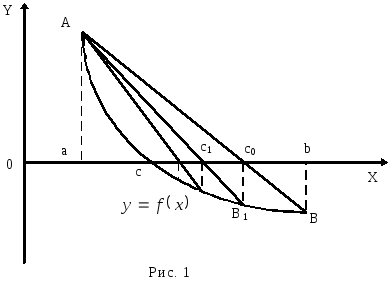
Сначала находится уравнение хорды АВ:
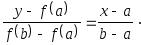
Для точки пересечения ее с осью абсцисс (x=c0, y=0) получается уравнение
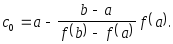
Далее сравниваются знаки величин
 (a)
и
(a)
и
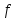 (с0)
и для рассматриваемого случая оказывается,
что корень находится в интервале (a,
c0),
так как
(с0)
и для рассматриваемого случая оказывается,
что корень находится в интервале (a,
c0),
так как
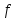 (a)
(a)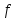 (с0)<0.
Отрезок [c0,b]
отбрасывается. Следующая итерации
состоит в определении нового приближения
c1
как точки
пересечения хорды АВ1
с осью абсцисс и т.д. Итерационный
процесс продолжается до тех пор, пока
значение
(с0)<0.
Отрезок [c0,b]
отбрасывается. Следующая итерации
состоит в определении нового приближения
c1
как точки
пересечения хорды АВ1
с осью абсцисс и т.д. Итерационный
процесс продолжается до тех пор, пока
значение
 (cn)
не станет по модулю меньше заданного
числа
(см. подраздел
3.1).
(cn)
не станет по модулю меньше заданного
числа
(см. подраздел
3.1).Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех его применения, как и метода бисекции, гарантирован.
В лабораторной работе №4 предлагается, используя программы - функции HORDA и Round из файла methods.cpp (файл заголовков metods.h, директория LIBR1), найти корень уравнения
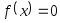 с
заданной точностьюEps
методом хорд, исследовать скорость
сходимости и обусловленности метода.
с
заданной точностьюEps
методом хорд, исследовать скорость
сходимости и обусловленности метода.Для данной работы, как и для лабораторной работы №3 задаются индивидуальные варианты нелинейных уравнений (см. подраздел 3.6).
Порядок выполнения лабораторной работы №4:
Графически или аналитически отделить корень уравнения
 (т.е. найти отрезки[Left,
Right], на которых
функция
(т.е. найти отрезки[Left,
Right], на которых
функция
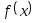 удовлетворяет
условиям применимости метода).
удовлетворяет
условиям применимости метода).Составить подпрограмму - функцию вычисления функции
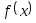 ,
предусмотрев округление значений
функции с заданной точностьюDelta
с использованием программы Round.
,
предусмотрев округление значений
функции с заданной точностьюDelta
с использованием программы Round.Составить головную программу, вычисляющую корень уравнения
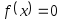 и
содержащую обращение к подпрограммеf(x),
HORDA,
Round и индикацию
результатов.
и
содержащую обращение к подпрограммеf(x),
HORDA,
Round и индикацию
результатов.Провести вычисления по программе. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода.
В подразделе 3.7 приводится текст программы - функции HORDA, предназначенной для решения уравнения
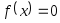 методом хорд.
методом хорд.
3.4. Метод Ньютона (Лабораторная работа № 5)
В случае, когда известно хорошее начальное приближение решения уравнения
 ,
эффективным методом повышения точности
является метод Ньютона. Он состоит в
построении итерационной последовательности
,
эффективным методом повышения точности
является метод Ньютона. Он состоит в
построении итерационной последовательности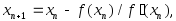 сходящейся к корню уравнения
сходящейся к корню уравнения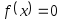 .
Достаточные условия сходимости метода
формулируются теоремой, приведенной
в[1,7].
.
Достаточные условия сходимости метода
формулируются теоремой, приведенной
в[1,7].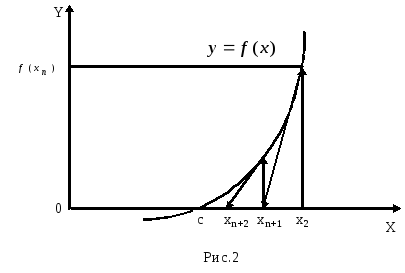
Метод Ньютона допускает простую геометрическую интерпретацию (рис. 2). Если через точку с координатами
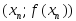 провести
касательную, то абсцисса точки пересечения
этой касательной с осью Ох будет
очередным приближением xn+1
корня
уравнения
провести
касательную, то абсцисса точки пересечения
этой касательной с осью Ох будет
очередным приближением xn+1
корня
уравнения
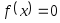 .
.Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством
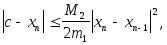
где М2-наибольшее значение модуля второй производной
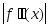 на отрезке[a,b];
m1-наименьшее
значение модуля первой производной
на отрезке[a,b];
m1-наименьшее
значение модуля первой производной
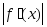 на отрезке[a,b].
Таким образом,
если
на отрезке[a,b].
Таким образом,
если
 то
то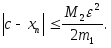 Это означает, что при хорошем начальном
приближении корня после каждой итерации
число верных десятичных знаков в
очередном приближении удваивается,
т.е. процесс сходится очень быстро
(имеет место квадратическая сходимость).
Из указанного следует, что при
необходимости нахождения корня с
точностью
итерационный процесс можно прекращать,
когда
Это означает, что при хорошем начальном
приближении корня после каждой итерации
число верных десятичных знаков в
очередном приближении удваивается,
т.е. процесс сходится очень быстро
(имеет место квадратическая сходимость).
Из указанного следует, что при
необходимости нахождения корня с
точностью
итерационный процесс можно прекращать,
когда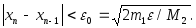 (3.1)
(3.1)Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближение xn-1 не удовлетворяет условию окончания процесса, то вычисляются величины
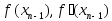 и следующие приближение корня
и следующие приближение корня При выполнении условия(3.1)
величина xn
принимается
за приближенное значение корня с,
вычисленное с точностью .
При выполнении условия(3.1)
величина xn
принимается
за приближенное значение корня с,
вычисленное с точностью .В лабораторной работе № 5 предлагается, используя программы-функции NEWTON и ROUND из файла methods.cpp (файл заголовков methods.h, директория LIBR1), найти корень уравнения
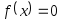 с заданной
точностью Eps
методом Ньютона, исследовать скорость
сходимости и обусловленность метода.
с заданной
точностью Eps
методом Ньютона, исследовать скорость
сходимости и обусловленность метода.Для данной работы вид функции
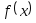 задается
индивидуально каждому студенту
преподавателем из числа вариантов,
приведенных в подразделе 3.6.
задается
индивидуально каждому студенту
преподавателем из числа вариантов,
приведенных в подразделе 3.6.Порядок выполнения лабораторной работы №5.
Графически или аналитически отделить корень уравнения
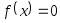 (т.е. найти отрезки[Left,
Right], на котором
функция
(т.е. найти отрезки[Left,
Right], на котором
функция
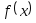 удовлетворяет условиям сходимости
метода Ньютона).
удовлетворяет условиям сходимости
метода Ньютона).Составить подпрограммы - функции вычисления
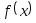 ,
,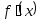 ,
предусмотрев округление их значений
с заданной точностьюDelta.
,
предусмотрев округление их значений
с заданной точностьюDelta.Составить головную программу, вычисляющую корень уравнения
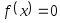 и содержащую обращение к подпрограммам
,
и содержащую обращение к подпрограммам
,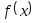 ,
,
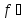 (x),
Round, NEWTON
и индикацию результатов.
(x),
Round, NEWTON
и индикацию результатов.Выбрать начальное приближение корня x0 из [Left, Right] так, чтобы

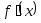 >0.
>0.Провести вычисления по программе. Исследовать скорость сходимости метода и чувствительность метода к ошибкам в исходных данных.
Для приближенного вычисления корней уравнения
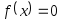 методом Ньютона предназначена программа
- функцияNEWTON,
текст которой представлен в подразделе
3.7.
методом Ньютона предназначена программа
- функцияNEWTON,
текст которой представлен в подразделе
3.7.
