
4676
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ Г.Ф. МОРОЗОВА»
МАТЕМАТИКА
Методические указания к выполнению расчетно-графических работ для студентов по направлению подготовки
09.03.02 – Информационные системы и технологии
Воронеж 2018
2
УДК 517 Сапронов, И. В. Математика [Электронный ресурс] : методические указания к
выполнению расчетно-графических работ для студентов по направлению подготовки 09.03.02 – Информационные системы и технологии / И. В. Сапронов, П. Н. Зюкин, Е. В. Раецкая ; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018. – 49 с.
Одобрено решением учебно-методического совета ФГБОУ ВПО «ВГЛТУ» (протокол № 6 от 23.03.2018)
Рецензент заведующий кафедрой высшей математики ФГБОУ ВО Воронежский ГПУ, д-р физ.-мат. наук, проф. В. В. Обуховский
В соответствии с рабочей программой при изучении дисциплины «Математика» предусмотрено выполнение расчетно-графических работ, направленное на закрепление теоретического материала и приобретение навыков решения задач, относящихся к основным разделам математического анализа и математической статистики.
Методические указания к выполнению расчетно-графических работ предназначены для студентов направления подготовки 09.03.02 – Информационные системы и технологии.
3
Оглавление
Введение....…………………………………………………………………..……...4
1.Расчетно-графическая работа № 1 «Полное исследование функций и построение графиков»……………………………………….……………….........5
1.1.Теоретическая часть……………………………………………….……………5
1.1.1.Некоторые теоремы о дифференцируемых функциях………….…………..5
1.1.2.Применение производной к исследованию функций…………………...….7
1.1.3.Полная схема исследования функции и построения графика………….…12
1.2.Практическая часть………………………………...………………………….13
1.3.Индивидуальные задания……………………………………………………..18
2.Расчетно-графическая работа № 2 «Математическая статистика»….…20
2.1.Теоретическая часть……………………………………...…………...……….20
2.2.Практическая часть……………………………………...……………...……..24
2.3.Индивидуальные задания……………………………………………...…...…33
Библиографический список ……………………………………..……….……..47 Приложение………………………………………………………………………..48
|
|
4 |
|
|
|
|
Введение |
|
|
В |
соответствии с |
учебным |
планом направления |
подготовки |
09.03.02 |
– Информационные |
системы |
и технологии, изучение |
дисциплины |
«Математика» предусматривает выполнение одной расчетно-графической работы в каждом семестре. Рабочая программа дисциплины «Математика» по данному направлению подготовки предусматривает расчетно-графические работы по разделам «Дифференциальное исчисление функций одной переменной», «Математическая статистика».
В данных методических указаниях по первому из разделов предложена расчетно-графическая работа «Полное исследование функций и построение графиков», при выполнении которой нужно провести полное исследование функций и построить их графики, по второму разделу предложена расчетнографическая работа «Математическая статистика», при выполнении которой нужно вычислить основные выборочные величины, выборочный коэффициент корреляции, определить доверительный интервал коэффициента корреляции, уравнение линейной регрессии, построить корреляционное поле и график линейной регрессии. Изложены необходимые теоретические сведения и разобраны примеры решения задач по каждой теме. Приведены варианты задач для выполнения расчетно-графических работ.
5
1. Расчетно-графическая работа № 1 «Дифференциальное исчисление функции одной переменной»
1.1. Теоретическая часть
1.1.1. Некоторые теоремы о дифференцируемых функциях
Здесь приводится ряд теорем, имеющих большое теоретическое и прикладное значение.
Теорема 1.1 (теорема Ролля).
Если функция y f (x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения (то есть f (a) f (b) ), то найдется хотя бы одна точка c , c (a,b) , в которой
производная f |
|
|
|
|
|
|
(x) обращается в нуль, то есть f |
(c) 0. |
|
|
|||
Замечание 1.1. Производная функции y f (x) в точке |
x есть угловой |
|||||
коэффициент |
касательной к графику |
функции |
y f (x) |
в точке |
x |
|
(геометрический смысл производной: f |
|
|
|
|
||
|
(x) tg ). |
|
|
|||
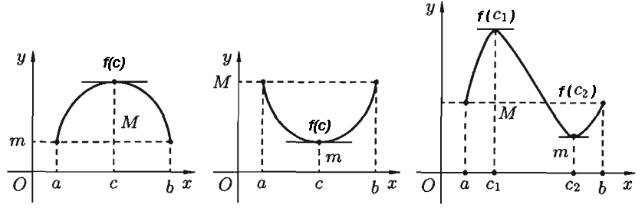
Геометрический смысл теоремы Ролля заключается в том, что на графике функции найдется такая точка, в которой касательная параллельна оси Ox , а именно точка с координатами (c, f (c)) , в которой tg f (c) 0
(см. рис 1.1).
Рис 1.1
6
Теорема 1.2 (теорема Лагранжа).
Если функция y f (x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) ), то найдется хотя бы одна точка c , c (a,b) , такая,
|
|
|
|
что выполняется равенство f (b) f (a) f (c)(b a) . |
|||
Последнее равенство называют формулой конечных приращений. Если |
|||
|
f (b) f (a) |
|
|
его преобразовать к виду |
|
f (c), то теорема Лагранжа получает |
|
b a |
|||
|
|
||
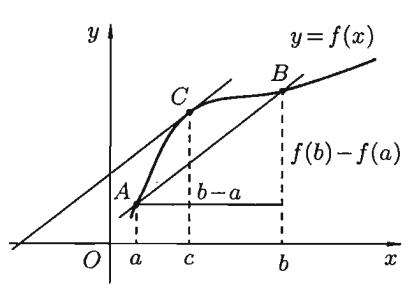
простой геометрический смысл: на графике функции y f (x) найдется точка
С с координатами (с, f (с)) , в которой касательная параллельна секущей – прямой, проходящей через точки A(a, f (a)) и B(b, f (b)) (см. рис 1.2).
Рис 1.2 Следствие 1.1. Если производная функции равна нулю на некотором
промежутке, то функция постоянна на этом промежутке.
Следствие 1.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются на постоянное слагаемое.
Теорема 1.3 (теорема Коши).
Если функции f (x) и (x) непрерывны на отрезке [a,b],
дифференцируемы на интервале (a,b) , причем (x) 0 во всех точках x

7
этого интервала, то найдется хотя бы одна точка c , c (a,b) , такая, что
|
f (b) f (a) |
|
|
|
|
|
|
|
выполняется равенство |
|
f (c) |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
(b) (a) |
|
|
|
|
|
|
|
|
|
(c) |
|
|
|
|
||
Далее приводятся способы раскрытия неопределенностей вида |
0 |
и |
|
, |
||||
|
|
|||||||
0 |
||||||||
которые основаны на применении производных.
Теорема 1.4 (правило Лопиталя раскрытия неопределенностей вида 00 ).
Пусть функции f (x) , (x) определены и дифференцируемы во всех
точках |
x некоторой окрестности точки x0 , кроме, |
возможно, |
точки x0 . |
||||||||
|
|
|
|
во всех точках |
x этой окрестности точки |
x0 |
(кроме, |
||||
Пусть (x) 0 |
|||||||||||
возможно, |
точки |
x0 ), |
lim f x lim x 0 |
и существует |
предел |
||||||
|
|
|
|
|
x x0 |
x x0 |
|
|
|
||
|
f |
|
|
|
|
|
|
|
|
|
|
lim |
(x) |
. Тогда |
lim |
f (x) |
|
. |
|
|
|
||
|
|
|
|
|
|
||||||
|
|
|
x x0 (x) |
|
|
|
|
||||
x x0 (x) |
|
|
|
|
|
||||||
Теорема 1.5 (правило Лопиталя раскрытия неопределенностей вида ).
Пусть функции f (x) , (x) определены и дифференцируемы во всех
точках |
x некоторой окрестности точки x0 , кроме, |
возможно, |
точки x0 . |
||||||||
|
|
|
|
во всех точках x |
этой окрестности точки |
x0 |
(кроме, |
||||
Пусть (x) 0 |
|||||||||||
возможно, |
точки |
x0 ), |
lim f x |
lim x |
и существует |
предел |
|||||
|
|
|
|
|
x x0 |
x x0 |
|
|
|
||
|
f |
|
|
|
|
|
|
|
|
|
|
lim |
(x) |
. Тогда |
lim |
f (x) |
. |
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
x x0 (x) |
|
|
|
|
|||
x x0 (x) |
|
|
|
|
|
|
|||||
1.1.2. Применение производной к исследованию функций
8
Возрастание и убывание функции Теорема 1.6 (необходимые условия возрастания и убывания функции).
|
Если дифференцируемая на интервале (a,b) функция f (x) |
возрастает |
|
|
x интервала |
(убывает) на этом интервале, то f (x) 0 во всех точках |
||
(a,b) |
|
|
( f (x) 0 во всех точках x интервала (a,b) ). |
|
|
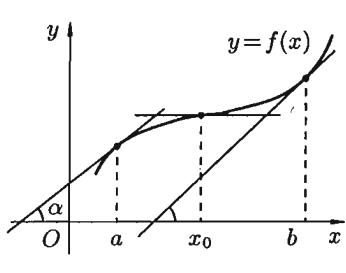
Геометрически эта теорема означает, что касательные к графику возрастающей функции образуют острые углы с положительным направлением оси (для убывающей функции эти углы – тупые) или в некоторых точках параллельны оси Ox (см. рис 1.3).
Теорема 1.7 (достаточные условия возрастания и убывания функции).
Если функция |
f (x) дифференцируема на интервале (a,b) |
и |
|
|
f (x) 0 |
||||
во всех точках x |
этого интервала, то функция |
f (x) возрастает на |
||
интервале (a,b) . |
|
|
|
|
Если функция |
f (x) дифференцируема на интервале (a,b) |
и |
|
|
f (x) 0 |
||||
во всех точках x этого интервала, то функция f (x) |
убывает |
на интервале |
||
(a,b) . |
|
|
|
|
Рис 1.3
9
Максимумы и минимумы функций (экстремумы функций)
Точка x0 называется точкой максимума функции y f (x) , если f (x0 ) f (x) для любых значений x из некоторой - окрестности точки x0 .
Значение функции в точке максимума называется максимумом функции (см.
рис 1.4).
Точка x0 называется точкой минимума функции y f (x) , если f (x0 ) f (x) для любых значений x из некоторой - окрестности точки x0 .
Значение функции в точке минимума называют минимумом функции (см. рис
1.4).
Точки максимума и минимума называют точками экстремума функции. Максимумы и минимумы функции называют экстремумами функции.
Рис 1.4
Теорема 1.8. (необходимое условие существования экстремума).
Если x0 – точка экстремума функции f (x) и функция f (x)
дифференцируема в этой точке, то f (x0 ) 0 .
Геометрически условие f (x0 ) 0 означает, что в точке x0 существует касательная к графику функции, параллельная оси Ox .
|
|
10 |
Точки |
x0 , |
входящие в область определения функции f (x) вместе с |
некоторой |
своей |
|
окрестностью, в которых f (x0 ) 0 или производная |
функции f (x) не существует, назовем критическими точками функции. Эти точки называют также подозрительными на экстремум. Последняя теорема утверждает, что точками экстремума функции могут быть лишь критические точки этой функции.
Обратная теорема неверна: существуют точки, в которых производная равна нулю (касательная параллельна оси Ox ), но эти точки не являются точками экстремума. Существуют функции, которые в точках экстремума не имеют производных.
Теорема 1.9 (достаточные условия экстремума).
Пусть функция f (x) непрерывна на некотором интервале, содержащем критическую точку x0 , и дифференцируема во всех точках этого интервала,
кроме, возможно, точки x0 . Если при переходе слева направо через точку x0
производная меняет знак, то x0 – точка экстремума функции f (x) .
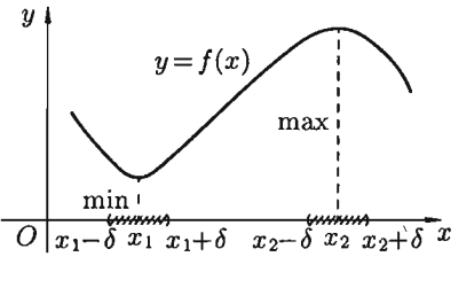
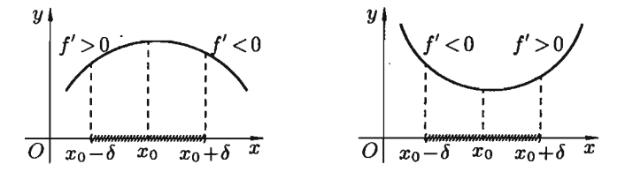
Если знак меняется с плюса на минус, то x0 – точка максимума функции (рис
1.5). Если знак меняется с минуса на плюс, то x0 – точка минимума функции
(рис 1.6).
Исследовать функцию на экстремум означает найти все ее экстремумы.
Рис 1.5 |
Рис 1.6 |
