
4676
.pdf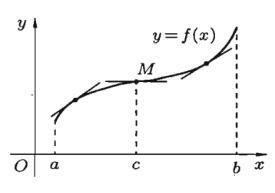
|
|
11 |
|
|
|
Выпуклость графика функции. Точки перегиба |
|
|
|||
График дифференцируемой |
функции |
y f (x) |
называется |
выпуклым |
|
(выпуклым вверх) на |
интервале (a,c) , если он расположен ниже любой ее |
||||
касательной на этом интервале (рис 1.7). |
|
|
|
||
График дифференцируемой |
функции |
y f (x) |
называется |
вогнутым |
|
(выпуклым вниз) на |
интервале |
(c,b) , если он расположен выше любой ее |
|||
касательной на этом интервале (рис 1.7).
Рис 1.7
Точка графика непрерывной функции y f (x) , отделяющая выпуклую часть графика от вогнутой части графика, называется точкой перегиба графика (точка M на рис 1.7).
Интервалы выпуклости и вогнутости находят с помощью следующей теоремы.
Теорема 1.10 (достаточные условия выпуклости и вогнутости).
Если во всех точках интервала (a,b) функция y f (x) имеет отрицательную вторую производную, то есть f (x) 0 , то график этой функции является выпуклым (выпуклым вверх) на интервале (a,b) .
Если во всех точках интервала (a,b) функция y f (x) имеет положительную вторую производную, то есть f (x) 0 , то график этой функции является вогнутым (выпуклым вниз) на интервале (a,b) .
Точки перегиба находят с помощью следующих теорем.
12
Теорема 1.11 (необходимое условие существования точки перегиба).
Если x0 – абсцисса точки перегиба графика функции y f (x), то либо f (x0 ) 0 , либо производная второго порядка функции f (x) в точке x0 не существует.
Из последней теоремы следует, что точками перегиба графика непрерывной функции y f (x) могут быть лишь те точки графика, в
абсциссах которых производная f x равна нулю или не существует.
Теорема 1.12 (достаточные условия существования точки перегиба).
Пусть функция y f (x) непрерывна в точке x0 , имеет производную
второго порядка во всех точках некоторой окрестности точки x0 , |
кроме, |
||
возможно, самой точки x0 , |
f (x0 ) 0 или |
f (x0 ) не существует. |
Пусть |
при переходе через точку x0 |
производная f |
|
|
(x) меняет знак. Тогда точка |
|||
графика функции y f (x) с абсциссой x0 является точкой перегиба графика.
1.1.3. Полная схема исследования функции и построения графика
Исследование функции последовательности.
y f (x) целесообразно вести в определенной
1.Найти область определения функции.
2.Выяснить, является ли функция четной или нечетной.
3.Найти точки пересечения графика функции с осями координат (или установить, что их нет).
4.Исследовать функцию по производной первого порядка (интервалы монотонности, точки экстремума).
5.Исследовать функцию по производной второго порядка (выпуклость, вогнутость, точки перегиба графика).
6.Найти вертикальные асимптоты графика функции (или установить, что
их нет).
7.Найти невертикальные асимптоты графика функции (или установить, что их нет).
8.На основании проведенного исследования построить график функции.
9.Определить множество значений функции.
13
Приведенная схема исследования не является обязательной. Иногда (в более простых случаях) достаточно выполнить лишь несколько операций, например 1, 3, 4. В более сложных случаях можно дополнительно исследовать функцию на периодичность, построить дополнительно некоторые точки графика, выявить другие особенности функции. Иногда целесообразно сопровождать исследование поэтапным построением графика или отдельных его частей.
1.2. Практическая часть
Пример |
1. Исследовать методами дифференциального исчисления |
||||||
функцию y |
5x2 |
|
и на основании полученных результатов построить еѐ |
||||
x2 |
25 |
||||||
график. |
|
|
|
|
|
|
|
Решение. |
Проведем исследование функции y |
5x2 |
по следующей |
||||
x2 25 |
|
||||||
схеме:
1. Область определения функции.
В область определения исследуемой функции не входят лишь те значения
x , для |
которых x2 25 0 , то |
есть |
x 5 |
и x 5. |
Поэтому |
||
D( y) ( ; 5) ( 5;5) (5; ) . |
|
|
|
|
|
||
2. Вид функции. |
|
|
|
|
|
|
|
Выясним, является ли функция четной или нечетной. |
|
||||||
Если |
y( x) y(x) |
для любого |
x |
из |
области |
определения |
функции |
y f (x) , |
то эта функция называется четной. График четной |
функции |
|||||
симметричен относительно оси ординат. |
|
|
|
|
|
||
Если |
y( x) y(x) |
для любого |
x |
из |
области |
определения |
функции |
y f (x) , то эта функция называется нечетной. График нечетной функции
симметричен относительно начала координат. |
|
|
|
|
|
||||||
Для нашей функции: |
|
|
|
|
|
|
|
|
|||
|
5x2 |
|
5( x)2 |
5x2 |
|
5x2 |
|||||
y(x) |
|
, |
y( x) |
|
|
|
, |
y(x) |
|
. |
|
x2 25 |
( x)2 25 |
x2 25 |
x2 25 |
||||||||
14
Видим, что y( x) y(x) для любого x из области определения функции. Поэтому функция четная, еѐ график симметричен относительно оси ординат.
3. Точки пересечения графика функции с осями координат.
Для нахождения точек пересечения графика с осью Ox решим систему
уравнений |
|
|
|
|
|
|
y 0, |
|
|||
|
|
|
5x2 |
|
|
|
|
|
|
||
y |
|
|
|
. |
|
x |
2 |
25 |
|||
|
|
|
|
||
Отсюда получаем, что x 0 , |
y 0. Следовательно, точка (0;0) является |
||||
точкой пересечения графика функции с осью Ox .
Для нахождения точки пересечения графика функции с осью Oy решим
систему уравнений |
|
|
|
|
|
|
|
|
|
x 0, |
|
|
|||
|
|
|
|
5x2 |
|
|
|
|
|
|
|
|
|
||
|
y |
|
|
|
|
. |
|
|
x |
2 |
|
|
|||
|
|
|
|
25 |
|||
Отсюда x 0 , |
y 0, поэтому точка |
(0;0) является точкой пересечения |
|||||
графика функции с осью Oy . |
|
|
|
|
|
|
|
4. Исследование функции по производной первого порядка (интервалы монотонности, точки экстремума).
Найдем первую производную функции:
|
5x2 |
|
|
|
|
(5x2 ) (x2 25) 5x2 (x2 |
25) |
|
10x (x2 25) 5x2 2x |
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
(x |
25) |
|
|
|
|
|
|
|
|
|
|
(x |
25) |
|
|
|||||||
x |
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
10x (x2 |
25 x2 ) |
|
|
250x |
|
|
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(x2 25)2 |
|
|
(x2 25)2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y 0 при |
x 0 , |
y |
не существует при |
x 5 |
|
|
и |
x 5 . |
Точки |
x1 5 , |
||||||||||||||||||||||
x2 0 , x3 |
5 |
разбивают область определения функции на четыре интервала |
||||||||||||||||||||||||||||||
( ; 5) , |
( 5;0) , |
(0;5) , (5; ) . Определим знак производной |
y |
на каждом из |
||||||||||||||||||||||||||||
них. Возьмем любое число из |
|
интервала |
( ; 5) , |
например |
6 . |
Так как |
||||||||||||||||||||||||||
|
250 ( 6) 1500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y ( 6) |
|
|
|
|
|
12,4 0 , поэтому |
на |
всем |
интервале |
( ; 5) |
||||||||||||||||||||||
(36 25)2 |
121 |
|
||||||||||||||||||||||||||||||
производная |
y 0 |
и, |
следовательно, |
|
функция |
|
монотонно возрастает. |
|||||||||||||||||||||||||
Аналогично определяем знак производной y на трех других интервалах: |
|
|||||||||||||||||||||||||||||||

|
|
15 |
|
|
|
|
|
|
|
|||
y ( 1) |
250 ( 1) |
|
250 |
|
0,4 0 , |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
(1 25)2 |
576 |
|
|
|
|||||
y (2) |
250 2 |
|
|
500 |
|
|
1,1 0 , |
|||||
(4 25)2 |
441 |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
y (7) |
|
250 7 |
|
|
|
1750 |
3,1 0 . |
|||||
(49 25)2 |
|
|
||||||||||
|
|
|
|
576 |
|
|
||||||
Результаты исследования занесем в таблицу:
x |
( ; 5) |
( 5;0) |
0 |
(0;5) |
(5; ) |
|
|
|
|
|
|
y |
+ |
+ |
0 |
− |
− |
|
|
|
|
|
|
y |
|
|
0 |
|
|
|
|
|
|
|
|
y |
функция |
функция |
|
функция |
функция |
|
|
max |
|
|
|
|
возрастает |
возрастает |
|
убывает |
убывает |
|
|
|
|
|
|
Итак, функция возрастает на каждом из интервалов ( ; 5) , ( 5;0) и убывает на интервалах (0;5) , (5; ) . В точке x2 0 производная меняет знак с «+» на «−», следовательно, x2 0 − точка максимума функции. Значение функции в этой точке ymax(0) 0 .
5. Исследование функции по производной второго порядка (выпуклость,
вогнутость, точки перегиба графика). Найдем вторую производную функции:
|
250x |
|
|
|
(x) (x2 25)2 |
x ((x2 25)2 ) |
|
||||
|
|
|
|
||||||||
y ( y ) |
|
|
|
|
|
250 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
4 |
||||
|
(x |
25) |
2 |
|
(x |
25) |
|
||||
|
|
|
|
|
|
|
|
||||
250 |
1 (x2 |
25)2 2x (x2 25) |
2x |
250 |
(x2 |
25) (x2 25 4x2 ) |
|
|
|
(x2 25)4 |
|
|
(x2 25)4 |
||||
|
|
|
|
|
|
|
||
|
|
250 |
3x |
2 25 |
. |
|
|
|
|
|
(x2 |
25)3 |
|
|
|
||
|
|
|
|
|
|
|
||
16
y 0 , если 3x2 25 0 . Это уравнение не имеет решения.
y не существует при x 5 и |
x 5. |
|
Точки x1 5, |
x3 5 разбивают |
область определения функции на три |
интервала: ( ; 5) , ( 5;5) , (5; ) . Определим знак производной y на каждом
|
|
3 62 |
25 |
250 |
|
133 |
274,8 0 , поэтому на всем |
||
|
(62 25)2 |
|
|
|
|||||
из них. Так как y ( 6) 250 |
121 |
||||||||
интервале ( ; 5) |
производная |
y 0 и, |
следовательно, график функции |
||||||
является вогнутым на данном интервале. Аналогично определяем, что y 0 на
интервале |
( 5;5) , поэтому график выпуклый на данном интервале. На |
интервале |
(5; ) y 0 , поэтому график вогнутый на этом интервале. |
Результаты исследования занесем в таблицу:
x |
( ; 5) |
( 5;5) |
(5; ) |
|
|
|
|
y |
+ |
− |
+ |
|
|
|
|
y |
|
|
|
|
|
|
|
y |
вогнутый |
выпуклый |
вогнутый |
|
|
|
|
|
график |
график |
график |
|
|
|
|
Точек перегиба на графике функции нет.
6. Вертикальные асимптоты графика функции
Исследуемая функция имеет две точки разрыва. Это точки x1 5 и x3 5, в которых функция не определена. Вычислим пределы функции в точке x1 5 слева и справа:
|
5x2 |
|
5x2 |
||
lim |
|
, lim |
|
|
. |
|
|
|
|||
x 5 x2 25 |
x 5 x2 |
25 |
|||
x 5 |
|
x 5 |
|
|
|
17
Поэтому прямая с уравнением x 5 является вертикальной асимптотой графика функции. Аналогично, так как
|
5x2 |
|
5x2 |
||
lim |
|
, lim |
|
|
, |
|
|
|
|||
x 5 x2 25 |
x 5 x2 |
25 |
|||
x 5 |
|
x 5 |
|
|
|
то прямая с уравнением x 5 является вертикальной асимптотой графика функции.
7. Невертикальные асимптоты графика функции.
Невертикальной асимптотой будем называть асимптоту, не параллельную оси Oy . Невертикальная асимптота графика функции y f (x) при x (при x ) существует тогда и только тогда, когда существуют конечные пределы
lim |
f x |
k , |
|||
x |
|||||
x |
|
||||
( lim |
|
f x |
k , |
||
|
|
||||
x |
x |
1 |
|||
|
|||||
lim f x kx b
x
lim f x kx b1).
x
Эта асимптота имеет уравнение y kx b |
( y k1x b1). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Вычислим пределы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
5x2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
f x |
|
|
|
|
|
|
5x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|||||||||
lim |
|
lim |
|
lim |
|
|
|
lim |
|
x |
|
|
|
|
0 k , |
|||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x |
x |
x x |
25 |
x x2 |
25 |
|
x |
25 |
|
|
1 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
5x |
2 |
|
|
|
|
|
|
5x |
2 |
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
||||
lim f x kx lim |
|
|
|
0 x |
lim |
|
|
|
lim |
|
|
|
|
|
5 b . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
x |
|
|
x x2 25 |
|
x x2 |
25 |
x |
|
|
|
25 |
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так |
как оба предела |
k и b |
конечны, |
то |
график |
|
|
функции имеет |
||||||||||||||||||||||||
невертикальную |
асимптоту при |
x . |
Еѐ |
уравнение y kx b , |
то есть |
|||||||||||||||||||||||||||
y 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично устанавливаем, |
что прямая с уравнением |
y 5 является |
||||||||||||||||||||||||||||||
невертикальной асимптотой графика функции при x .
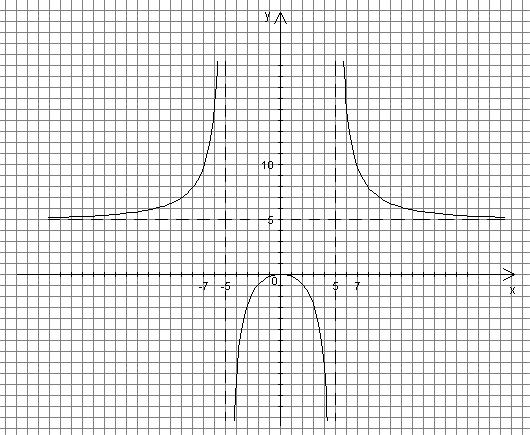
8. Построение графика функции.
На основании результатов проведенного исследования строим график функции.
18
Четность функции облегчает построение графика: строим часть графика функции для значений x [0;5) (5; ) , а затем отображаем эту часть графика симметрично относительно оси ординат и получаем весь график.
Для уточнения графика рассмотрим несколько дополнительных точек:
|
5 22 |
|
20 |
|
|
|
5 72 |
245 |
|
||||
y(2) |
|
|
|
|
|
|
0,9 , |
y(7) |
|
|
|
|
10,2 . |
22 |
25 |
|
|
|
|
|
|||||||
|
|
21 |
|
|
72 25 |
24 |
|
|
|||||
Рис. 1.8
9. Множество значений функции.
Вид графика (см. рис. 1.8) позволяет сделать вывод, что множество значений функции E( y) ( ;0] (5; ) .
1.3. Индивидуальные задания
Исследовать методами дифференциального исчисления функции и на основании полученных результатов построить их графики.

19
1. |
а) |
y |
2x 1 2 |
|
; |
|
|||
|
|
|
2x 4 |
|
|
|
y |
x 1 2 |
|
2. |
а) |
|
; |
|
3 2x x2 |
||||
3.а) y 1 x3 ;
x2
4.а) y x 2 3 ;
x 1 22
5. |
а) |
y |
|
1 |
|
|
; |
|
|
|
|
||||
x2 4x |
|
|
|||||
|
|
|
3 |
||||
6. |
а) y x 2 3 |
|
; |
|
|||
|
|
|
|
3x2 |
|
|
|
7. |
а) |
y |
x 1 2 |
; |
|
||
4 |
2x |
|
|||||
|
|
|
|
|
|
||
8. |
а) |
y |
4 x 2 |
|
; |
|
|
4 2 x |
|
||||||
|
|
|
|
|
|||
9.а) y x2 2x ;
x1
10. а) |
y |
|
x3 |
; |
|
|
|
||
x2 1 |
|
|
|
|
|||||
11. а) |
y |
|
x2 |
; |
|
|
|
||
x2 1 |
|
|
|
|
|||||
12. а) |
y |
|
x3 4 |
; |
|
|
|
||
|
3x2 |
|
|
|
|||||
|
|
|
|
|
|
|
|||
13. а) |
y |
1 |
|
|
|
; |
|||
|
|
|
|
|
|
|
|||
|
x2 2x |
2 |
|||||||
|
|
|
|
||||||
|
y |
x 1 |
2 |
|
|
||||
14. а) |
|
|
|
; |
|
|
|||
|
|
|
|||||||
|
|
x 2 |
|
|
|
|
|||
б) y ln x 1 . x 2
б) y x 1 e 2x .
б) y 1 . ex 1
б) y ln 2x2 3 .
б) y ln x 12 x2 .
б) y x2 ln x .
б) y 1 . e2x 1
б) y x ln x 1 .
б) y x3e x .
б) y ln x2 9 .
б) |
y |
ex e x |
. |
||||||
ex e x |
|||||||||
|
|
|
|
||||||
|
y |
|
|
x |
|
||||
б) |
|
|
|
|
. |
|
|||
ln |
|
|
|
|
|||||
|
x |
|
|||||||
б) y xe x .
б) y xe x2 .

20
15.а)
16.а)
17.а)
18.а)
19.а)
20.а)
21.а)
22.а)
23.а)
24.а)
25.а)
y |
x 3 |
2 |
; |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|||||||||||||||
|
x |
|
|
|
|
|
|
|
||||||||||||
y |
|
|
|
x3 |
|
|
|
|
|
; |
|
|
|
|||||||
|
6 2x2 |
|
|
|
||||||||||||||||
y |
|
|
|
x3 |
|
|
|
|
; |
|
|
|
|
|
||||||
|
2x2 |
|
8 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
y |
|
x2 |
x 4 |
; |
||||||||||||||||
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x2 x |
3 |
|
|
|||||||||||||||
y |
2 |
; |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2x 1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
y |
|
|
|
x4 |
; |
|
|
|
|
|
|
|
|
|
||||||
|
x3 1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
4 |
|
1 |
|
|
|
; |
|
|
|
|
|
||||||||
|
|
x4 |
|
|
|
|
|
|||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
y x |
|
|
|
; |
|
|
|
|||||||||||||
x 2 |
|
|
|
|
||||||||||||||||
y |
|
|
x |
|
; |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
y 3 x2 ; x 2
y2x2 1 ; x4
б) y ln 4 x2 .
б) y ln 1 2x .
б) y x2 2ln x .
б) y xln x .
б) y 2 x2 e x2 .
б) y ln x2 9 .
|
|
1 |
|
|
|
x2 |
|
||||
|
y |
|
|
||||||||
б) |
|
|
|
|
|
|
|
e 2 . |
|||
|
|
|
|
|
|
|
|||||
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
||||
б) |
y |
ex |
. |
|
|
|
|
||||
|
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
||||
б) |
y |
ln x |
. |
|
|
|
|||||
|
|
|
|
||||||||
|
|
|
|
|
x |
|
|
|
|||
1
б) y e x .
б) y e x2 .
2.Расчетно-графическая работа № 2 «Математическая статистика»
2.1.Теоретическая часть
